№14.14. Продифференцировать функцию:
1) 
; 2) 
3) 
№14.15. Найти производную функции 
в точке 
:
; 
.
№14.16. На кривой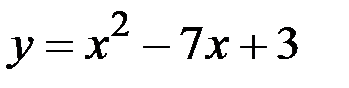 
найти точку, в которой касательная параллельна прямой 
.
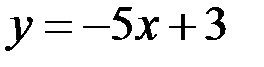№14.17. Написать уравнения касательных к кривым 
и 
, проведенных через точки пересечения этих кривых.
№14.18. В каких точках касательная к графику функции 
образует с осью Ох угол 
?
№14.19. Исследовать функцию на монотонность: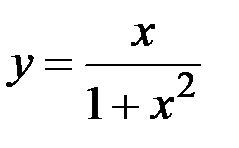 
.
№14.20. Найти экстремумы функции: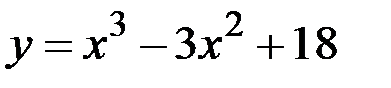 
.
№14.21. Найти наибольшее и наименьшее значения функции
на отрезке 
.
№14.22. Исследовать функцию и построить ее график;
1) 
2) 
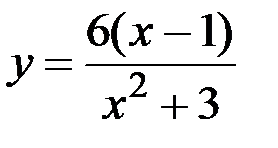
Занятие 15. ПЛАНИМЕТРИЯ
№15.1. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки длиной 5 и 12 см. Найти катеты треугольника.
№15.2. В прямоугольный треугольник c катетами 
и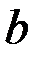 
вписан квадрат, имеющий с треугольником общий прямой угол. Найти периметр квадрата.
№15.3. Дан треугольник со сторонами 12, 15 и 18. Проведена окружность, касающаяся обеих меньших сторон и имеющая центр на большей стороне. Найти отрезки, на которые центр окружности делит большую сторону треугольника.
№15.4. Стороны треугольника равны 13, 14 и 15см. Найти отношение площадей описанного и вписанного в этот треугольник кругов.
№15.5. Через вершину прямого угла прямоугольного треугольника с катетами 6 и 8 см проведен перпендикуляр к гипотенузе. Вычислить площади образовавшихся треугольников.
№15.6. В равнобедренном треугольнике с боковой стороной, равной 4см, проведена медиана боковой стороны. Найти основание треугольника, если медиана равна 3см.
№15.7. Найти диагональ и боковую сторону равнобокой трапеции с основаниями 20 и 12 см, если известно, что центр описанной окружности лежит на большем основании трапеции.
№15.8. Из точки А, не лежащей на окружности, проведены к ней касательная и секущая. Расстояние от точки А до точки касания равно 16 см, а до одной из точек пересечения секущей с окружностью равно 32см. Найти радиус окружности, если секущая удалена от ее центра на 5см.
№15.9. Дана точка Р, удаленная на 7см от центра окружности с радиусом 11см. Через эту точку проведена хорда длиной 18см. Какова длина отрезков, на которые делится хорда точкой Р?
№15.10. Длина параллельных сторон трапеции равна 25 и 4см, а длины непараллельных сторон 20 и 13см. Найти высоту трапеции.
№15.11. Периметр ромба равен 2см, длина его диагоналей относится как 3:4. Найти площадь ромба.
№15.12. Данный квадрат со стороной а срезан по углам так, что образовался правильный восьмиугольник. Определить площадь этого восьмиугольника.
№15.13. В параллелограмме с периметром 32см проведены диагонали. Разность между периметрами двух смежных треугольников равна 8см. Найти длины сторон параллелограмма.
№15.14. Один из углов трапеции равен 
, а прямые, содержащие боковые стороны трапеции, пересекаются под прямым углом. Найти длину меньшей боковой стороны трапеции, если ее средняя линия равна 10см, а одно из оснований 8см.
№15.15. Стороны треугольника относятся как 5:4:3. Найти отношение отрезков сторон, на которые они делятся точкой касания вписанной окружности.
Задания для самостоятельного решения
№15.16. В треугольнике основание равно 60см, высота 12см и медиана, проведенная к основанию, 13см. Определить боковые стороны.
№15.17. Вычислить площадь трапеции, параллельные стороны которой 16 и 41см, а непараллельные 17см и 25см.
№15.18. Один из катетов прямоугольного треугольника равен 15см, а радиус окружности, вписанной в этот треугольник, равен 3см. Найти площадь треугольника.
№15.19. Определить площадь треугольника, если две стороны соответственно равны 27см и 29см, а медиана третьей стороны равна 26см.
№15.20. Определить боковые стороны равнобочной трапеции, если ее основания и площадь равны соответственно 8см, 14 см и 44см2.
№15.21. В прямоугольном треугольнике АВС из вершины В прямого угла опущена высота ВД на гипотенузу АС. Известно, что АВ=13, ВД=12. Найти площадь треугольника.
№15.22. Прямые, содержащие боковые стороны равнобедренной трапеции, пересекаются под прямым углом. Найти длины всех сторон трапеции, если ее площадь равна 12см 
, а длина высоты равна 2см.
№15.23. В треугольнике АВС отрезок AD – биссектриса, угол С равен 1050, угол CAD равен 70. Найдите угол В. Ответ дайте в градусах.
№ 15.24. В треугольнике АВС угол С равен 900, АВ = 18, cosA = 0,5. Найдите АС.
№15.25. В треугольнике АВС АВ = ВС, АС = 5, cosC = 0,8. Найдите высоту СН.
№15.26. Высоты треугольника АВС пересекаются в точке Н. Известно, что отрезок СН равен радиусу окружности, описанной около треугольника. Найдите угол АСВ.
Занятие 16. СТЕРЕОМЕТРИЯ
№16.1. Из вершины А прямоугольника АВСД проведён к его плоскости перпендикуляр АМ, конец которого отстоит от других вершин на расстояния 6. 7 и 9 см. Найти длину АМ.
№16.2. Точка М, лежащая вне плоскости данного прямого угла, удалена от его вершины В на расстояние а, а от каждой стороны на расстояние в. Определите расстояние от точки М до плоскости прямого угла.
№16.3. Из точки А, отстоящей от плоскости α на расстояние а, проведены две наклонные АВ и АС под углом 300, причём их проекции ОВ и ОС составляют угол 1200. Определите расстояние между концами наклонных.
№16.4. Стороны треугольника 15 см, 37 см и 44 см. Из вершины большего угла треугольника проведён к его плоскости перпендикуляр длиной 16 см. Найти расстояния от концов перпендикуляра до большей стороны треугольника.
№16.5. Вычислите угол между диагональю куба и плоскостью его основания.
№16.6. Ребро куба равно ℓ. Найти кратчайшее расстояние от диагонали до непересекающего её ребра.
№16.7. В прямом параллелепипеде АВСДА1В1С1Д1 АВ = 29, АД = 36, ВД = 25, боковое ребро 48. Найти площадь сечения АВ1С1Д.
№16.8. В правильной треугольной призме сторона основания равна а, боковое ребро 2а. Найти площадь сечения, проведённого через сторону одного и центр другого основания.
№16.9. 122-миллимитровая бомба даёт при взрыве воронку диаметром в 4 м и глубиной 1,5 м. Какое количество земли (по весу) выбрасывает бомба? 1 м3 земли весит 1650 кг.
№16.10. В правильной четырёхугольной пирамиде SABCD точка О – центр основания, S – вершина, SО = 54, АС = 144. Найдите боковое ребро SВ.
№16.11. Прямоугольный параллелепипед описан около цилиндра, радиус и высота которого равны 2. Найдите объём параллелепипеда.
№16.12. Объём цилиндра равен 1 см3. Радиус основания уменьшили в 2 раза, а высоту увеличили в 3 раза. Найдите объём получившегося цилиндра. Ответ дайте в см3.
№16.13. В кубе АВСDA1B1C1D1 найдите угол между прямой АВ1 и плоскостью АВС1.
№16.14. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, стороны основания которой равны 4, а боковые рёбра равны 3, найдите расстояние от точки В до прямой C1D1.
