Запропонована структура схема та проведено математичне моделювання процесу аерозольного нанокаталізу. Отримані відповідні статичні та динамічні математичні моделі з метою впровадження в контури системи автоматизації керування процесом аерозольного нанокаталізу.
Огляд літератури. Дослідження теоретичних основ процесів хімічної технології, широке застосування програмно-технічних засобів (ПТЗ) створюють умови для переходу на якісно нові методи аналізу та проектування систем керування. При цьому зменшуються витрати на створення проміжних, дослідно-конструкторських установок, збільшується надійність та екологічна безпека проектних рішень.
В даний час однією з пріоритетних задач промислової екології є кваліфікована утилізація хлорорганічних відходів виробництва і споживання. Продукція підприємств хлорорганічного синтезу є суттєвим фактором ризику як для навколишнього середовища, так і для здоров’я людини [1].
Екологічна безпека тісно пов’язана з безпекою функціонування хімічно небезпечних об’єктів і залежить від багатьох факторів - надійність систем автоматизації, протиаварійного захисту та ін. Огляд літератури показав, що автоматизація процесів нанохімічних технологій знаходиться на початковому етапі свого розвитку [2].
Застосування процесу аерозольного нанокаталізу в промислових масштабах стримується через відсутність ефективної системи автоматизації. Актуальною задачею у зв’язку з цим є подальший розвиток наукових досліджень в області автоматизації процесів аерозольного нанокаталізу з застосуванням сучасних методів керування та ПТЗ, що дозволило б суттєво підвищити екологічну безпеку утилізації відходів хлорорганічного синтезу.
Постановка задачі. Для розробки дворівневої системи автоматизації керування (САК) процесом аерозольного нанокаталізу необхідно отримати відповідно статичні та динамічні математичні моделі підсистем процесу. Статичні математичні моделі необхідні для визначення оптимальних завдань для контурів керування, динамічні – для синтезу регуляторів у цих контурах.
Рішення задачі. Моделювання як метод дослідження ТП є важливим етапом при проектуванні систем автоматизації керування. На основі розробленої моделі виконується аналіз компонентів об’єкта керування та вирішуються питання оптимізації.
Для побудови математичного опису багатозв’язних об’єктів керування доцільним є використання декомпозиції, тобто поділу об’єкта керування на підсистеми у відповідності з особливостями загальної технологічної схеми процесу [3].
Експериментально-аналітичний метод аналізу полягає в проведені планових експериментів на діючому об’єкті активним або пасивним способом [4]. На основі отриманих результатів експерименту визначають залежність:
Y=f(x1,x2,…xn), (1)
| де | Y – вихідний параметр; |
| x1, x2, …, xn – вхідні параметри. |
Для ефективного рішення задачі функціонування системи автоматизації необхідно отримати математичний опис процесу з метою організації роботи в оптимальних режимах за енерготехнологічними та економічними показниками, що забезпечували б при цьому екологічну безпеку навколишнього середовища.
За своєю природою процеси, що протікають в реакторі аерозольного нанокаталізу, є детермінованими, тобто такими, при яких вихідні параметри однозначно встановлюються значеннями вхідних величин.
Вибір методу дослідження для побудови математичних моделей підсистем визначається:
а) характером поставленої задачі;
б) умовами проведення експерименту, що допускаються за технологічними вимогами;
г) діапазонами відхилення параметрів, що досліджується;
д) характером експлуатаційних збурень.
Хіміко-технологічний процес аерозольного нанокаталізу супроводжується переміщенням матеріальних потоків вхідних реагентів при їх взаємодії. Особливе значення в задачі математичного моделювання такого процесу набуває опис руху потоків з урахуванням кінетики хімічної реакції. До найбільш важливих особливостей процесу аерозольного нанокаталізу слід також віднести велику швидкість протікання реакцій в реакторі при високих температурах та суттєво нелінійні залежності між вхідними та вихідними параметрами реактора.
Структурна схема побудови математичної моделі процесу аерозольного нанокаталізу передбачає детальне дослідження рівнянь кінетики реакцій на основі експериментально-аналітичних даних для більш глибшого розуміння процесу аерозольного нанокаталізу з метою розробки методів керування (рис. 1).
|
| Рис. 1. Структурна схема побудови математичної моделі процесу аерозольного нанокаталізу |
Математична модель являє собою систему рівнянь, яка відображає суть явищ, що протікають в об’єкті керування, і яка за допомогою відповідних алгоритмів дозволяє прогнозувати поведінку об’єкта керування при зміні вхідних параметрів та параметрів керування.
На практиці при складанні математичного опису користуються наближеним уявленням про внутрішню структуру потоків. З одного боку це полегшує постановку граничних умов для рівнянь, а з другого - дозволяє намітити конкретні експериментальні дослідження для знаходження параметрів керування рухом потоків.
Для об’єкта керування опис руху потоків розглядається у більшості випадків з точки зору переміщення і розподілення реагентів в потоці. Гідродинамічну модель, яка підлягає аналізу, записують переважно в вигляді рівнянь, які характеризують зміну концентрації реагентів в потоці.
У кожний момент часу реагенти реакції зв’язані матеріальним балансом. Основа матеріального балансу - стехіометричне (мольне) рівняння.
Рівняння матеріального балансу на елементарній ділянці довжини трубчатого реактора отримуємо наступним чином: швидкість подачі даного компонента на ділянку ∆х складає mY, швидкість його виходу з ділянки ∆х дорівнює:
, (2)
| де | m – мольна витрата газової суміші на вході в реактор; |
| Yi – мольна доля компонента у газовій суміші. |
Загальна швидкість реакції на ділянці ∆х (швидкість реакції – об’єм):
, (3)
| де | D – діаметр реактора. |
Матеріальний баланс газу на ділянці:
. (4)
Рівняння приведене для моделювання:
. (5)
Виходячи з рівняння матеріального балансу, розрахована питома вага кожного компонента в процентному відношенні на прикладі діхлоретану (ДХЕ), які наведено в табл. 1.
Таблиця 1
Матеріальний баланс процесу аерозольного нанокаталізу
| Найменування | % об’єму |
| Вхідні реагенти | |
| ДХЕ (C2H4Cl2) | |
| Кисень (O2) | |
| Вихідні продукти | |
| Вуглекислий газ (CO2) | 49,4 |
| Соляна кислота (HCl) | 40,4 |
| Вода (H2O) | 10,2 |
При моделюванні процесів хімічної технології в матеріальні та теплові баланси входять рівняння хімічної кінетики, які є предметом досліджень при вивченні механізму і умов оптимального проведення хімічних реакцій.
Витрати компонентів, що подаються в реактор, обчислювались за формулою:
, (6)
| де | Fпов. - витрати повітря (г/год); FДХЕ - витрати ДХЕ (г/год); K1 - коефіцієнт наявності кисню в повітрі (K 1= 0,2095); λ – коефіцієнт стехиометричного відношення (λ =1,0248). |
Умови, при яких реалізується модель змішування, виконуються, якщо у всьому потоці або на ділянці, що розглядається, проходить повне змішування частинок потоку.
Рівняння, що описує зміну концентрації в зоні змішування, має вигляд:
, (7)
| де | V – об’єм зони змішування, м3; |
 - швидкість потоку, що поступає в зону змішування, м3/год;
| |
| х(0), х – концентрація речовини на вході і в зоні змішування, кмоль/м3; | |
| t - час, год. |
Значення концентрації в зоні змішування і на виході з неї описується рівнянням:
, (8)
| де | х(0) – значення концентрації в зоні змішування в початковий момент часу; |
 - середній час перебування частинок потоку в зоні змішування.
|
Таким чином, для оптимального керування необхідно визначити оптимальний час перебування реагентів в реакторі 
опт., оптимальну температуру реакції Топ т, оптимальну концентрацію каталізатора Скат.опт ., оптимальне співвідношення реагентів, що беруть участь в реакції.
Математичний опис реактора змішування може бути отримано з загальних рівнянь гідродинаміки для випадку змішування:
, (9)
| де | q –інтенсивність речовин, |
та рівняння, що враховує температуру джерела тепла в потоці:
, (10)
якщо підставити в них відповідні вирази для інтенсивності джерел маси та тепла. Інтенсивність джерел маси в даному випадку дорівнює швидкості утворення вихідних речовин реакції.
Припускаючи, що в процесі хімічної реакції число молей реагентів не змінюється, знаходимо рівняння для реагентів реакції:
 ,
 ,
| (11) | |
| де | ω – швидкість утворення компонентів реакції. | |
При наявності теплового ефекту реакції система рівнянь (11) має бути доповнена відношенням, що визначає характер зміни температури в зоні реакції, яке можна отримати з рівняння (10).
Щоб урахувати теплообмін реагентів з зовнішнім теплоносієм, використаємо рівняння для джерела тепла:
, (12)
| де | qT – інтенсивність джерела тепла; |
| Q r – сумарний тепловий ефект реакцій, що протікають в реакторі; | |
| QT – швидкість теплопередачі, |
та рівняння теплового ефекту реакції і теплопередачі:
, (13)
| де | ср - теплоємність реагентів у потоці; |
| КТ - коефіцієнт теплопередачі; | |
| F – поверхня теплообміну, віднесена до одиниці об’єму. |
При записі виразу (13) припускаємо, що теплоємність ср реагентів в ході хімічної реакції не змінюється.
Сумісне рішення системи рівнянь (11) і (13) визначає при зроблених припущеннях поведінку реактора змішування у випадку нестаціонарних режимів.
Щоб отримати систему рівнянь для стаціонарного режиму, достатньо в рівняннях (11) і (13) вважати похідні по часу рівними нулю.
Згідно з цим, система рівнянь стаціонарного режиму реактора набуває наступного вигляду:
, 
(14)
. (15)
З отриманих рівнянь для стаціонарного режиму знайдемо значення концентрації реагентів і температури в реакторі при заданих значеннях вхідних концентрацій реагентів хi(0), температури суміші Т(0), яка подається до реактора, та температури теплоносія Тх.
Система рівнянь (14) і (15) може бути записана в більш зручному вигляді, якщо ввести позначення для середнього часу (часу контакту) перебування реагентів в реакторі:
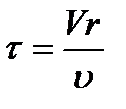. (16)
З урахуванням (16) рівняння (14) і (15) набудуть вигляду:
, (17)
. (18)
Слід зазначити, що процес аерозольного нанокаталізу, з точки зору кінетики, неможливо віднести ні до режиму змішування, ні до режиму витиснення. Керування в реакторі змішування зводиться до підтримки заданої температури, яка забезпечує оптимальний вихід цільового продукту, а в реакторі нанокаталізу додається такий важливий параметр керування як вібрація.
У реакторі нанокаталізу реагенти, що вступають в реакцію, змінюють концентрацію в кожній точці потоку внаслідок хімічної реакції та масообміну.
Час перебування реагентів в реакторі (Τ, с), константа швидкості (k, с-1) та швидкість реакції по реагентах (W, г/(м3р.о.·с) розраховувались за наступним рівнянням:
Τ = Vр. в./ VПГС, (19)
| де | Vр.в. – вільний об’єм реактора, м3; |
| VПГС – витрати парогазової суміші, м3/с, |
k=1/Τ·ln(1/(1 – xa)), (20)
| де | xa – ступінь перетворення компонента, |
W=C0·ха/ Τ, (21)
| де | C0 – початкова концентрація компонента, г/м3р .об. |
Отримані рівняння та розрахунки застосовуються як уставки на верхньому рівні системи автоматизації технологічного процесу аерозольного нанокаталізу.
Графічний інтерфейс процесу аерозольного нанокаталізу зі значеннями уставок подано на рис. 2.
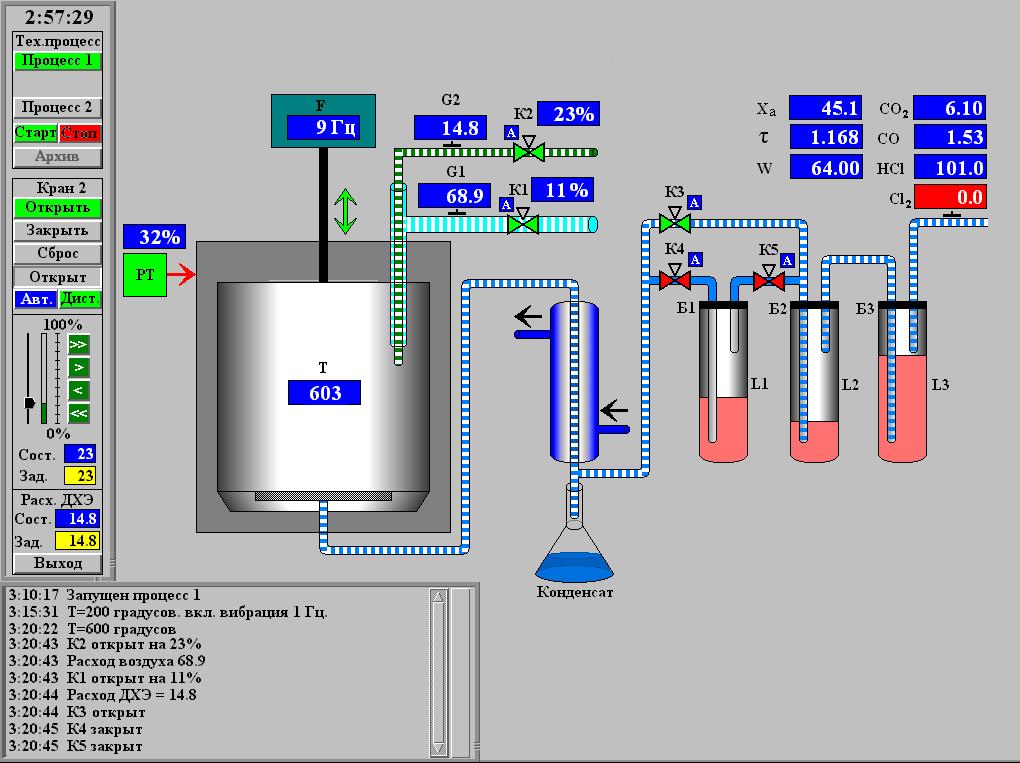
Рис. 2. Графічний інтерфейс процесу аерозольного нанокаталізу
Висновки. Обмеженість теоретичних відомостей про об’єкт керування визначила необхідність використання експериментально-аналітичних методів його дослідження, які дозволили отримати наступні результати:
1. На підставі рівнянь матеріального балансу визначені необхідні кількісні співвідношення компонентів для подачі в реактор нанокаталізу, що дає можливість розрахунку статичних режимів роботи підсистем процесу аерозольного нанокаталізу.
2. На основі математичного опису реактора змішування і загальних рівнянь гідродинаміки визначені рівняння для стаціонарного та динамічного режимів роботи технологічного процесу.
3. Розглянуті кінетичні рівняння дозволили визначити час перебування реагентів у реакторі, константу швидкості та швидкість реакції по реагентах, що є параметрами для прийняття рішення в підсистемах системи автоматизації та аргументами функцій для розрахунку поточних режимів роботи технологічного процесу.
4. Згідно з результатами дослідження запропонована математична модель процесу аерозольного нанокаталізу може бути використана при розробці алгоритмів та програмного забезпечення САК.
Список літератури:
1. Рязанцев А.И. Система экологического мониторинга окружающей среды / А.И. Рязанцев, В.С Кардашук // Радіоелектроніка Інформатика Управління. – Запоріжжя: ЗНТУ. - 2006. - № 2(16). - C. 128-132.
2. Сергеев Г.Б. Нанохимия: учебное пособие / Г.Б. Сергеев. – [2-е изд.]. – М.: КДУ, 2007. - 336 с.: ил.
3. Рязанцев О.І. Побудова математичної моделі технологічного процесу аерозольного нанокаталізу у віброзрідженному шарі для організації керування / О.І. Рязанцев, В.С. Кардашук // Вісник Східноукраїнського національного університету імені Володимира Даля. - Луганськ, 2009. - № 6(136). - Ч.1. - С. 274-279.
4. Рязанцев А.И. Математические методы исследования экспериментальных данных в системах управления процессами утилизации отходов химических производств по технологии нанокатализа / А.И. Рязанцев, В.С. Кардашук // Вісник Східноукраїнського національного університету імені Володимира Даля. - Луганськ, 2008. - № 12(130). - Ч.1. - С. 10-16.
УДК 519.876.5
Смирнов Г.М., Смирнова О.С.
