Разработана математическая модель реактора идеального перемешивания с переменным временем пребывания за счет изменения плотности реакционной массы для непрерывного нитрования бензола. Рис. 3, Табл. 3, Ист. 9.
Нитробензол – один из крупнотоннажных продуктов органического синтеза, исходное вещество для получения анилина и его производных [1-3]. Основным методом его промышленного производства служит нитрование бензола смесью азотной и серной кислот в непрерывно действующем реакторе перемешивания. Поскольку реакция нитрования протекает, как гетерогенный гетерофазный процесс, для реализации необходимо наличие интенсивного перемешивания [4]. Поэтому нитраторы с хорошей степенью точности можно считать реакторами идеального перемешивания.
Хотя математическое описание процессов в реакторах идеального перемешивания хорошо известно [5], их рассмотрение ограничено случаем, когда плотность входного и выходного потока является постоянной, и время пребывания потока в системе не зависит от глубины реакции. В реакции нитрования плотности входных и выходных потоков могут существенно изменяться с глубиной реакции за счет изменения плотности как кислотной, так и органической фаз. В связи с этим возникает вопрос: насколько сильно этот эффект влияет на степень превращения бензола в реакторе и, соответственно, нужно ли его учитывать при моделировании процесса нитрования.
Целью настоящего исследования является выявление количественной зависимости плотности нитромассы в реакторе в зависимости от степени превращения и температуры, разработка модели реактора идеального перемешивания с изменяемой плотностью реакционной массы и описание на этой основе макрокинетики нитрования бензола в промышленном реакторе, проведение сравнительного численного моделирования степени превращения с учетом и без учета эффекта изменения плотности.
1. Зависимость плотности нитромассы от степени превращения и температуры
Нитромасса в процессе нитрования бензола состоит из смеси двух взаимно нерастворимых жидкостей:
а) кислотной части – раствора серной кислоты, азотной кислоты и воды;
б) органической части – раствора нитробензола в бензоле.
В промышленном нитровании используются следующие начальные соотношения между реагентами на входе в реактор [6]:
- бензол – 1 кмоль,
- азотная кислота – 1,03 кмоль;
- серная кислота – 1,2 кмоль;
- вода – 1,5 кмоль.
В процессе нитрования в соответствие с реакцией (1):
С6H6 + HNO3 = C6H6NO2 + H2O, (1)
в кислотной части происходит уменьшение концентрации азотной кислоты и увеличение концентрации воды, а в органической части снижение концентрации бензола и увеличение концентрации нитробензола.
При расчете и моделировании зависимости плотности нитромассы от температуры и степени превращения использовали следующие предположения:
а) раствор нитробензола в бензоле считали идеальным и аддитивным (объем раствора равен сумме объемов компонентов);
б) пренебрегали растворимостью неорганических кислот в органической фазе и протеканием динитрования бензола. Как отмечено в [6], эти величины в условиях промышленного мононитрования малы.
В связи с тем, что кислотная и органическая составляющая нитромассы взаимно нерастворимы, плотность нитромассы (r, кг×м-3)рассчитывали по аддитивной схеме по формуле:
, (2)
где mor., mac. – массы органической и кислотной частей, кг;
Vor., Vac. – их объемы, м3.
Массы рассчитывали на 1 кмоль исходного бензола, с учетом степени превращения бензола (a, %), исходя из материального баланса процесса по формулам (3) и (4)
, (3)
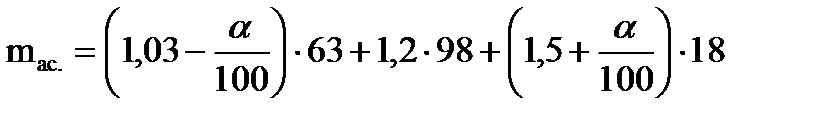, (4)
где 123; 78; 63; 98; 18 – соответственно, молярные массы нитробензола, бензола, азотной кислоты, серной кислоты, воды, кг×кмоль-1.
Объем кислотной части рассчитывали по формуле:
, (5)
в которой плотность кислотной части рассчитывали по формуле многокомпонентных растворов электролитов (6) [7]:
, (6)
где r0 – плотность воды, кг×м-3;
n – количество компонентов-электролитов в растворе;
ci – концентрация і-го электролита, % масс.;
t – температура, оС.
Значения коэффициентов A 1 i, A 2 i, A 3 i приведены в табл. 1.
Плотность воды при температуре t (0-150oC) рассчитывали по формуле (7) [7]:
(7)
где t*=0,01×t; R1=15,910174; R2 = -73,840671; R3=141,693443;
R4=-297,162815; R5=160,758796; R6=146,727674; R7=-194,580793; R8=58,847919.
Относительная погрешность формулы (7) составляет 0,0048 % [8].
Коэффициенты А 1, А 2, А 3 в уравнении (6) для серной и азотной кислот (по данным [8]).
Таблица 1
| Вещество | А 1 | А 2 | А 3 |
| НNO3*) | 5,7225 | -0,0127 | 0,0165 |
| H2SO4 | 6,3787 | -0,0076 | 0,0363 |
Примечание *) Для диапазона концентраций азотной кислоты 0-50 % масс. при температурах 0-100оС
Объем органической части рассчитывали по аддитивной формуле:
, (8)
где 
- масса бензола, кг;
- масса нитробензола, кг;
rb, rnb – плотности бензола и нитробензола, кг×м-3
Для учета влияния температуры мы обработали литературные данные [8] по плотности бензола и нитробензола при разных температурах. Как следует из данных, приведенных на рис. 1, в обоих случаях в широком диапазоне температур наблюдаются линейные зависимости плотности от t. В результате обработки данных методом наименьших квадратов были получены следующие уравнения (9) и (10), соответственно для плотности бензола и нитробензола. В скобках указаны значения коэффициентов детерминации, которые указывают на качество линейной зависимости.
(R2=99,96 %); (9)
(R2=100%) (10)
Поскольку R2 указывает на долю отклонений от общего среднего, которые могут быть объяснены наличием линейной зависимости, их близость к 100% свидетельствует о высокой степени соответствии моделей (9) и (10) реальности в диапазоне температур от 0 до 120оС.
Рис. 1 Зависимость плотности бензола (1) и нитробензола (2) (r, кг×м-3) от температуры (t, oC) (по данным [8])
Используя рассмотренную модель, мы рассчитали зависимость плотности нитромассы на выходе из нитратора в зависимости от степени превращения бензола и температуры. Результаты расчетов представлены в табл. 2. Как следует из этих данных, с увеличением степени превращения происходит заметное увеличение плотности, в среднем на 5-7 %. Вместе с тем с увеличением температуры наблюдается понижение плотности. Наблюдается своеобразный компенсационный эффект: если в нитратор загружаются ингредиенты с низкой температурой, например 20оС, а выходящая нитромасса имеет повышенную температуру (60-70оС), то их плотности оказываются достаточно близкими (1314 и 1344, табл. 2). То есть увеличение плотности за счет степени превращения в нитробензол в какой-то мере может компенсироваться снижением ее за счет возрастания температуры
Полученные результаты ставят следующий вопрос, связанный с технологией нитробензола. Вследствие изменения плотности в реакторе будет наблюдаться изменение среднего времени пребывания. Поэтому необходимо выявить, насколько существенным является этот эффект и к каким последствиям он может приводить.
2 Модель реактора идеального перемешивания с переменным временем пребывания.
Рассмотрим реактор идеального перемешивания с рабочим объемом V м3, в который поступает исходная смесь с исходной концентрацией бензола С0 кмоль×м-3, плотностью r0 кг×м-3 и объемной скоростью v0 м3×с-1. Из реактора выходит нитромасса с концентрацией С1 кмоль×м-3, плотностью r1 кг×м-3 и объемной скоростью v1 м3×с-1 (рис. 2). В реакторе протекает химическая реакция со скоростью (по абсолютной величине) W(C) кмоль×м-3×с-1.
Таблица 2
Зависимость плотности нитромассы на выходе из нитратора от степени превращения (Р) и температуры
| Р, % | Температура, оС | ||||||||
Рис. 2 Модель идеального перемешивания с переменной плотностью
В соответствие с общим подходом к получению модели идеального перемешивания [5,9] рассмотрим поведение системы за малый промежуток времени dt. За этот промежуток времени в систему поступит С0×v0×dt×кмоль исходного вещества (бензола), а из системы выйдет с выходным потоком С1×v1×dt×кмоль бензола. В системе за этот промежуток времени прореагирует W(С1)×V×dt кмоль бензола. Отсюда накопление бензола в объеме нитратора:
. (11)
Разделим обе части (11) на V, получим выражение для приращения концентрации бензола в нитраторе и на выходе из него (в силу идеального перемешивания):
(12)
Разделив обе части (2.12) на dt и перейдя к пределу: 
получаем дифференциальное уравнение реактора:
. (13)
Для нахождения неизвестной величины v1 составим дифференциальное уравнение для изменения плотности. За время dt в систему поступило r0×v0×dt кг исходной смеси и вышло r1×v1×dt кг конечной нитромассы. Накопление массы в нитраторе за время dt составит:
(14)
Разделим обе части уравнения (2.14) на объем V, получим уравнение для приращения плотности:
(15)
Плотность реакционной массы является функцией степени превращения, а через нее – функцией концентрации бензола. Поэтому, после деления (15) на dt и перехода к пределу 
получаем дифференциальное уравнение:
. (16)
Подставив в (16) выражение (13), получим:
. (17)
Из (17) можно выразить величину v1:
(18)
где 
- начальное время пребывания (время пребывания исходной смеси при условии неизменности температуры и отсутствия реакции), с.
Подставив (18) в (13), получаем окончательное дифференциальное уравнение реактора идеального перемешивания с изменяемой плотностью реакционной массы:
(19)
Рассмотрим частный случай уравнения (19), когда плотность не изменяется, то есть, когда 
. Подставив эти выражения в (19) после приведения подобных и сокращения получаем уравнение:
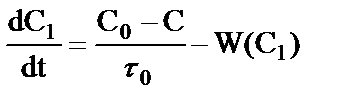, (20)
которое совпадает с известным выражением для реактора идеального перемешивания с одинаковой плотностью на входе и на выходе [5]. Таким образом, уравнение (19) является общим для описания макрокинетики в реакторе идеального перемешивания.
2.3 Моделирование степени превращения в нитраторе в стационарном режиме
После достижения стационарного режима 
дифференциальное уравнение (19) переходит в алгебраическое:
. (20)
При r=const (20) переходит в уравнение (21) для «обычного» реактора идеального перемешивания в стационарном режиме.
(21)
Рассмотрим, как сказывается изменение плотности реакционной массы на степени превращения в реакторе идеального перемешивания в процессе нитрования бензола в стационарном режиме.
Скорость гетерогенного нитрования бензола (W, кмоль м-3 с-1) описывается эмпирическим уравнением (22) [4,6]:
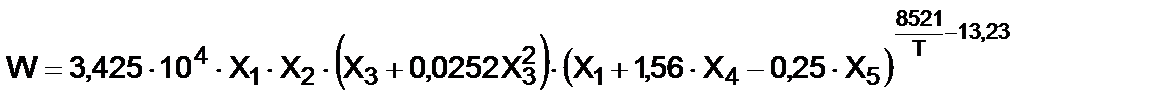(22)
где Х 1 – мольная доля азотной кислоты в кислотной фазе,
Х 2 – мольная доля бензола в органической фазе,
Х 3 – концентрация кислотной фазы в реакционной смеси, % об.,
Х 4 – мольная доля серной кислоты в кислотной фазе,
Х 5 – мольная доля воды в кислотной фазе,
Т – температура массы, К.
Для нахождения концентрации С1 и степени превращения необходимо, используя выражения (22), численно решить нелинейные алгебраические уравнения (20) и (21). Для нахождения зависимости 
мы для серии степени превращений от 0 до 100 % рассчитали значения плотности и молярной концентрации бензола и аппроксимировали полученные значения полиномом второго порядка по методу наименьших квадратов:
r(С1) = 1349,76750 – 15,58739∙ C 1 + 0,31774∙ C 12 (23)
Это уравнение хорошо описывает данные (рис.3): коэффициент детерминации R2 = 99,997 указывает, что отклонения от зависимости (23) малы.
Дифференцируя (23), находим:
Рис. 3. Зависимость плотности реакционной массы при 60оС от молярной концентрации бензола (точки) и аппроксимация по уравнению (23) (сплошная линия)
. (24)
Для расчетов по уравнениям (20) и (21) разработан расчетный проект MS Excel, в котором при заданной степени превращения и температуре рассчитывались: материальный баланс нитрования, плотность кислотного, органического слоев и реакционной массы, молярная концентрация бензола и скорость. Далее задавали время пребывания и решали обратную задачу – определяли степень, при которой уравнения (20) и (21) обращались в тождества с точностью |e| < 10-5. При моделировании исследовали, как влияет плотность массы на входе, которая, как показано выше, заметно зависит от температуры. Для этого в уравнении (20) использовали значение начальной плотности при 20 и 60оС. Температуру в реакторе принимали равной 60оС, что соответствует условиям нитрования в промышленном реакторе. Время пребывания изменяли от 1 до 1800 с. Результаты моделирования представлены в табл. 3
Отметим, что результаты моделирования находятся в хорошем качественном согласии результатами нитрования в промышленных условиях: практически реакция протекает в течение нескольких минут, а увеличение времени пребывания до 30 мин, и выше, необходимое для поддержания теплового режима, изменяет ее в небольшой степени [6].
Как следует из результатов табл. 2.3, влияние изменения плотности в процессе реакции практически не сказывается на степени превращения и выходной концентрации бензола в процессе нитрования. Это указывает, что изменения плотности демпфируются массой в реакторе, в чем проявляется инертность реактора идеального перемешивания.
Таблица 3
Результаты моделирования степени превращения (Р1, %) и концентрации бензола (С1, кмоль∙м-3) на выходе из реактора нитрования при 60оС без учета (по уравнению (21)) и с учетом влияния температуры на плотность (уравнение (20))
 ,с
| Моделирование по (21) | Моделирование по (20) | ||||
| 20oС | 60oС | |||||
| P | С1 | P | C1 | P | C1 | |
| 74,3 | 1,188 | 74,1 | 1,199 | 74,1 | 1,200 | |
| 78,0 | 1,021 | 77,8 | 1,030 | 77,8 | 1,031 | |
| 80,0 | 0,928 | 79,8 | 0,936 | 79,8 | 0,938 | |
| 82,4 | 0,817 | 82,3 | 0,825 | 82,2 | 0,826 | |
| 85,4 | 0,678 | 85,3 | 0,685 | 85,3 | 0,685 | |
| 88,2 | 0,552 | 88,0 | 0,558 | 88,0 | 0,558 | |
| 91,3 | 0,407 | 91,2 | 0,411 | 91,2 | 0,412 | |
| 93,3 | 0,313 | 93,2 | 0,317 | 93,2 | 0,317 | |
| 95,0 | 0,234 | 94,9 | 0,237 | 94,9 | 0,237 | |
| 97,1 | 0,137 | 97,0 | 0,139 | 97,0 | 0,139 | |
| 98,5 | 0,071 | 98,5 | 0,072 | 98,5 | 0,072 |
Из результатов можно сделать вывод, что при моделировании нитрования бензола можно пользоваться более простым уравнением (21), не учитывая изменений плотности нитромассы за счет разницы во входной и выходной температурах и изменении степени превращения.
Список литературы:
1. 1 Грейш А.А. Нитрование ароматических углеводородов на гетерогенных катализаторах [Текст] /А.А.Грейш//Рос. хим. журнал, 2004. – Т.48, № 6. – С. 92-104
2. 2 Жилин В.Ф. Синтез и технология нитропроизводных бензола и толуола [Текст]/ В.Ф.Жилин, В.Д.Збарский // Рос. хим. журнал, 2006. – Т.50, №3. – С.104-115
3. Горелик М.В. Химия и технология ароматических соединений [Текст]/ М.В.Горелик, Л.С.Эфрос // М.: Химия, 1992 – 640 с.
4. Biggs R.D. Rate of nitration of benzene [Текст]/ R.G.Biggs, R.R.White// Am. Ing. Chem. Educ. Journal, 1956. - №3. - p.26-33.
5. Coker A.K. Modeling of chemical reactions and reactor design [Текст] / Houston: Gulf Professional Publishing, 2001. – 1096 p.
6. Беркман Б.Е. Промышленный синтез ароматических нитросоединений и аминов [Текст] / Б.Е.Беркман // М.: Химия, 1964. – 344 с.
7. Асеев Г.Г. Электролиты. Физико-химические параметры концентрированных многокомпонентных систем [Текст] / Г.Г.Асеев, И.М.Рыщенко, А.С.Савенков.- Харьков: НТУ «ХПИ», 2005. – 448 с.
8. Плотность жидких веществ и водных растворов в зависимости от температуры в кг/м3 / НЕФТЬ-ГАЗ. Электронная библиотека [Электронный ресурс] – Режим доступа: http://www.oglib.ru/tabl/table10.html
9. Вольтер Б.В., Сальников И.Е. Устойчивость режимов работы химических реакторов. – М.: Химия, 1981. – 200 с.
УДК 681.513.2
Рязанцев О.І., Кардашук В.С.
