При отыскании оригинала по изображению в простейших случаях используют таблицу изображений основных элементарных функций и теоремы разложения.
Вторая теорема разложения позволяет найти оригинал по известному изображению, являющемуся дробно-рациональной функцией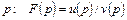 
, где 
и 
– многочлены от p соответственно степени m и n, причем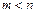 
. Если разложение на простейшие множители имеет вид 
, то, как известно, 
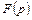может быть разложена на сумму элементарных дробей вида 
. Итак,
(3.1)
Все коэффициенты могут быть найдены по формуле
(3.2)
Вместо этой формулы для определения коэффициентов 
можно использовать элементарные приемы, применяемые в математическом анализе при интегрировании рациональных дробей. Если все корни многочлена простые, разложение упрощается: 
;
, где 
. (3.3)
После отыскания тем или иным способом разложения 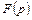на простейшие дроби оригинал 
находится так:
а) в случае кратных корней знаменателя
; (3.4)
б) в случае простых корней знаменателя
. (3.5)
Пример 1. Найти оригинал , если известно, что 
.
Решение. У изображения 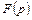в данном случае все корни знаменателя – действительные и простые. Поэтому лучше всего воспользоваться формулой (3.5). Имеем
.
Корни 
Отсюда по формуле (3.5) находим : 
.
Пример 2. Найти оригинал по его изображению 
.
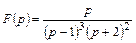Решение. Разложение 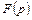на простейшие дроби имеет вид
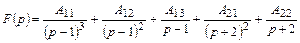(3.6)
Находим коэффициенты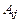 
по формуле (3.2)
Аналогично получим 
. Следовательно, 
. Отсюда по таблице изображений и теоремам смещения и линейности изображения имеем
Заметим, что коэффициенты разложения (3.6) можно найти и таким способом, который применялся в математическом анализе при интегрировании рациональных дробей.
3.4. Решение дифференциальных уравнений
и систем дифференциальных уравнений
операционным методом
Пусть дано линейное дифференциальное уравнение (ЛДУ) n -го порядка с постоянными коэффициентами
,
правая часть которого является оригиналом. Тогда и решение 
этого уравнения, удовлетворяющее начальным условиям 
(то есть решение задачи Коши для данного ЛДУ), тоже будет оригиналом.
Обозначим изображение искомого решения через 
, то есть 
. Используя теорему о дифференцировании оригинала и свойство линейности, находим изображение левой части исходного ЛДУ и приравниваем его к 
. В итоге вместо ЛДУ с начальными условиями получается так называемое изображающее уравнение, которое является линейным алгебраическим уравнением относительно новой неизвестной функции 
. Решая изображающее уравнение, находим . Определяя затем по 
оригинал , мы тем самым найдем искомое решение задачи Коши. Аналогично решаются и системы ЛДУ.
Пример 1. Решить ЛДУ 
, если 
.
Решение. Обозначим 
. По теореме о дифференцировании оригинала имеем 
. Тогда изображающее уравнение таково: 
. Отсюда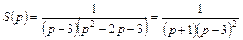 
. Восстановим теперь оригинал 
. Разложим вначале дробь 
на простейшие дроби: 
. Ищем A, B, C: 
. Полагая 
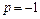, получаем 
, то есть 
; полагая 
, получаем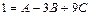 
, откуда 
.
Следовательно, 
.
Решение поставленной задачи Коши найдено.
Пример 2. Решить систему ЛДУ 
, если 
.
Решение. Обозначим 
и найдем изображения левой и правой частей каждого из уравнений системы.
Из последней линейной алгебраической системы уравнений находим неизвестную 
(например, по формулам Крамера)
.
Разложим на простейшие рациональные дроби: 
. Для определения чисел A, B, C получаем равенство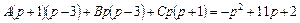 
.
Подставляя в обе части равенства вместо p поочередно числа –1; 3 и 0, имеем 
. Отсюда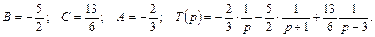 
Пользуясь таблицей изображений и свойством линейности изображения, найдем оригинал 
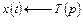. Итак, 
, одна из искомых функций найдена. Функцию можно найти аналогично 
, предварительно определив ее изображение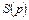 
. Но в данном случае можно найти проще, выражая из первого уравнения исходной системы ЛДУ
Задача решена.
КОНТРОЛЬНАЯ РАБОТА №3
