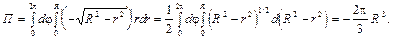а) Поверхностный интеграл I рода. Пусть F (x, y, z) - непрерывная функция и z = f (x, y) - гладкая поверхность S, где f (x, y) задана в некоторой области D плоскости xOy. Поверхностным интегралом I рода называется предел интегральной суммы при условии, что max dk ®0:
,
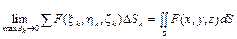где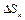 
- площадь k -го элемента поверхности S, точка 
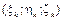принадлежит этому элементу, dk - диаметр этого элемента, F (x, y, z) определена в каждой точке поверхности S.
Значение этого интеграла не зависит от выбора стороны поверхности S, по которой производится интегрирование.
Если проекция D поверхности S на плоскость xOy однозначна, то соответствующий поверхностный интеграл I рода вычисляется по формуле
.
б) Поверхностный интеграл II рода. Пусть в декартовой системе координат Oxyz задана двусторонняяя поверхность S. Выберем определенную сторону поверхности S, задав определенное направление единичного вектора нормали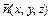 
, точка (x, y, z)Î S. И пусть в точках поверхности S определена вектор-функция 
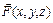с координатами P (x, y, z), Q (x, y, z), R (x, y, z). Сделав разбиение S на n частей Ti с площадямит Si, составим интегральную сумму вида
,
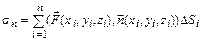где (xi, yi, zi)Î Ti;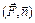 
означает скалярное произведение векторов 
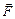и 
.
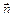Поверхностным интегралом II рода от вектор-функции 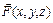по выбранной стороне поверхности S называется предел интегральной суммы s n при l®0 (l - диаметр разбиения), если этот предел существует; конечен, не зависит от способа разбиения и от выбора точек (xi, yi, zi). Обозначение:
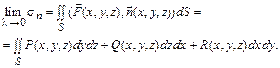
Физический смысл. Указанный интеграл выражает массу жидкости единичной плотности, протекающей через поверхность S в направлении вектора нормали 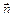со скоростью 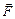за единицу времени, то есть так называемый поток вектор-функции (или векторного поля) 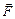через S в направлении .
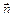2.6. Вычисление криволинейных интегралов
I и II рода
Пусть функция f (x, y, z) определена и непрерывна в точках дуги АВ кусочно-гладкой пространственной кривой. Если уравнение дуги АВ задано параметрическими уравнениями
x = x (t), y = y (t), z = z (t), (t 0£t£ t 1),
то
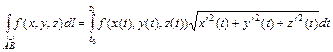(2.15)
В случае плоской кривой АВ
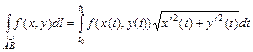. (2.16)
Механический смысл криволинейного интеграла I рода: если f (x, y, z)>0, то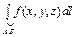 
представляет собой массу кривой, имеющей переменную линейную плотность m(r)= f (x, y, z).
Пример 1. Вычислить массу отрезка прямой, заключенного между точками А (0;-2), В (4;0), если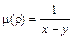 
.
Решение. Найдем уравнение прямой АВ: y =0,5 x -2; тогда 
.
Отсюда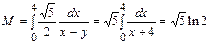 
.
Пусть функции P (x, y, z), Q (x, y, z), R (x, y, z) непрерывны в точках дуги АВ кусочно-гладкой пространственной кривой. Если уравнение дуги АВ задано параметрически x = x (t), y = y (t), z = z (t), (t 0£t£ t 1), то
(2.17)
В случае плоской кривой АВ
(2.18)
Пример 2. Найти работу силы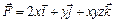 
вдоль части кривой 
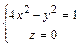(линия пересечения поверхносте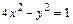й 
и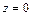 
) от точки 
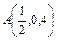до точки 
.
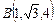Решение.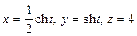 
. 
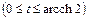– параметрическое задание пути 
. По формуле (2.17)
Пример 3. Вычислить работу силы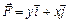 
вдоль части кривой 
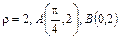. Движение от точки A к точке B – по ходу часовой стрелки.
Решение.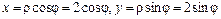 
– параметрическое задание части кривой (j в роли параметра t). По формуле (2.18)
.
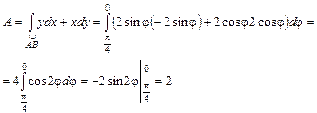2.7. Вычисление поверхностных интегралов I и II рода.
Связь между ними
а) Поверхностный интеграл I рода (ПОВИ-1). Если поверхность Т задана уравнением z = z (x, y), (x, y)Î D Ì Oxy, причем z (x, y) имеет непрерывные частные производные, а проекция D поверхности Т на плоскость Oxy имеет кусочно-гладкую границу, и если в точках поверхности Т задана непрерывная функция f (x, y, z), то интеграл от f (x, y, z) по площади поверхности Т (I рода) существует и вычисляется по формуле:
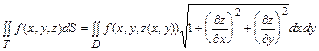(2.19)
(Справа в этой формуле стоит двойной интеграл).
Аналогичные формулы можно получить, проектируя поверхность T на другие координатные плоскости.
б) Поверхностный интеграл II рода (ПОВИ-2). Если поверхность Т задана так же, как в предыдущем пункте а), то поверхностный интеграл II рода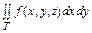 
существует и сводится к двойному интегралу по проекции D поверхности Т на плоскость Oxy следующим образом:
. (2.20)
Знак “+” в формуле (2.20) берется, если нормаль к выбранной стороне поверхности Т образует острый угол с осью Oz; знак “-” - в случае тупого угла.
Формулы, аналогичные (2.20), имеют место и для поверхностных интегралов II рода таких, как: 
. При этом нужно спроектировать поверхность Т на плоскости Oyz и Ozx соответственно.
в) Связь между ПОВИ-1 и ПОВИ-2). Имеет место формула
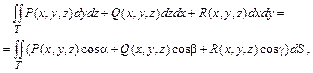(2.21)
связывающая поверхностные интегралы II рода (слева) и I рода (справа). Здесь a, b, g есть углы, образованные с осями Ox, Oy, Oz нормалью 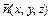к выбранной стороне поверхности Т в точке (x, y, z).
Пример1. Вычислить массу плоской пластины Т: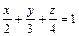 
, расположенной в I октанте (рис. 2.17) и имеющей поверхностную плотность 
.
Решение. Уравнение поверхности Т: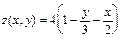 
(x, y)Î D есть проекция Т на плоскость Oxy. По формуле (2.19):
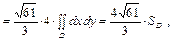
где SD – площадь фигуры D. А так как D – это D OAB, то – 
. Итак, 
(кг).
Пример 2. Вычислить поток П векторного поля 
(
- единичный направляющий вектор оси Oz) через верхнюю сторону нижней половины сферы Т: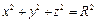 
.
Решение. Уравнение нижней полусферы:
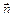. Нормаль к выбранной стороне образует острый угол с Oz, поэтому по формуле (2.20) имеем:
.
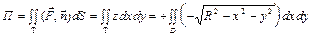Здесь D – проекция Т на плоскость Oxy есть круг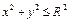 
. Пе-
рейдем в последнем двойном интеграле к полярным координатам x = r cosj, y = r sinj, 0£j£2p, 0£ r £ R. В итоге:
