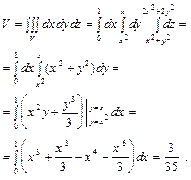Если f (x, y, z) - плотность распределения вещества по фигуре, то интеграл по этой фигуре выражает ее массу в соответствующих единицах измерения.
Замечание. Аналогично названным вводятся интегралы:
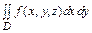- двойной интеграл по области D Î Oxy;
- криволинейный интеграл I рода по кривой Г Î Oxy.
Свойства интегралов по фигуре
(на примере тройного интеграла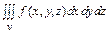 
).
1. Свойство линейности.
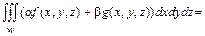
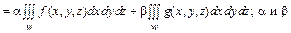-числа.
2. Если область W есть объединение двух областей W1 и W2, не имеющих общих внутренних точек, то
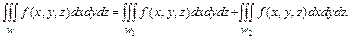
3. Если в области W: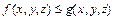 
, то
4. Теорема о среднем. Если f (x, y, z) непрерывна в замкнутой связной области W, то найдется точка (x *, y *, z *)Î W такая, что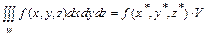 
, где V - объем тела W.
5. Если f(x,y,z)º1, то 
.
Предполагается, что все указанные интегралы существуют.
2.2. Вычисление двойных и тройных интегралов
в декартовых координатах
а) Двойной интеграл. Пусть область D плоскости Oxyz ограничена линиями y =j(x), y =y(x), x = a, x = b, где a < b, j(x)£y(x) и функции j, y непрерывны на отрезке [ a; b ] (рис.2.1). Двойной интеграл от непрерывной функции f (x, y) вычисляется путем сведения к двукратному интегралу по формуле
(2.1)
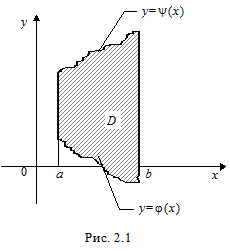
В выражении (2.1) сначала вычисляется 
при постоянном x. Полученный результат интегрируется по x.
Аналогично, если область D ограничена линиями x =a(y), x =b(y), y = c, y = d, где c < d, a(y)£b(y) и функции a и b непрерывны на отрезке [ c; d ] (рис.2.2), то
(2.2)
Замечание. В более общем случае область интегрирования разбивают на части, каждая из которых имеет один из рассмотренных видов.
Пример 1. Вычислить 
, где область ограничена линиями 
.
Решение. Указанные линии пересекаются в точках О (0,0) и А (1,-1) (рис. 2.3).
Применяя формулу (2.1) при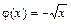 
, 
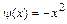, a =0, b =1, получим:
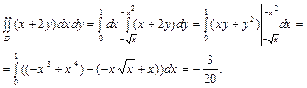
Пример 2. Изменить порядок интегрирования в двукратном интеграле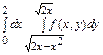 
.
Решение. Область интегрирования, ограниченную линиями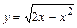 
, 
, x =2 (рис. 2.4), разобьем с помощью прямой y =1 на три области. Получим сумму интегралов:
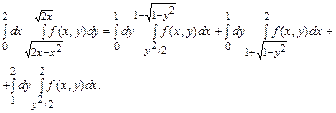
Здесь для определения пределов изменения переменной x уравнения 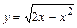, разрешены относительно x: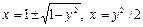 
.
Из свойств интеграла по фигуре следует, что площадь S плоской области D в декартовых прямоугольных координатах равна
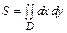. (2.3)
Пример 3. Вычислить площадь области, ограниченной линиями 
.
Решение. Имеем (рис. 2.5)
.
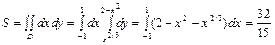Геометрический смысл двойного интеграла: объем V цилиндрического тела, ограниченного сверху непрерывной поверхностью z = f (x, y), (f >0), снизу плоскостью z =0 и с боков прямой цилиндрической поверхностью, вырезающей на плоскости Oxy область D, вычисляется по формуле
. (2.4)
Площадь S гладкой поверхности z = z (x, y), проектирующейся в область D плоскости Oxy, выражается формулой
. (2.5)
б) Тройной интеграл. Пусть пространственная область V в декартовой системе координат Oxyz ограничена снизу и сверху поверхностями z = F (x, y), z =F(x, y) (F (x, y)£F(x, y)), с боков прямой цилиндрической поверхностью и проектируется на плоскость Oxy в область D, ограниченную линиями y =j(x), y =y(x), x = a, x = b, (a < b, j(x)£y(x)), а функции F, F, j, y - непрерывны (рис.2.6).
|
Тройной интеграл от непрерывной функции f (x, y, z) вычисляется по формулам:
Замечание. Порядок интегрирования в последней формуле может быть изменен.
Пример 4. Вычислить тройной интеграл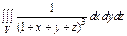 
, где область V ограничена поверхностями x + y + z =1, x =0, y =0, z =0.
Решение. Область V есть пирамида, ограниченная снизу плоскостью z =0, сверху плоскостью x + y + z =1 и с боков плоскостями x =0, y =0 (рис.2.7). Проекцией пирамиды на плоскость Oxy является треугольник, ограниченный прямыми x =0, y =0, x + y =1.
Для переменной z нижним пределом будет z =0 (плоскость Oxy), а верхним - значение z, полученное из уравнения плоскости x + y + z =1, то есть z =1- x - y. Поэтому получим:
Из свойств интеграла по фигуре следует, что объем V пространственной области V равен
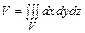. (2.6)
Пример 5. Вычислить объем тела, ограниченного поверхностями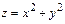 
, 
, 
, 
.
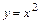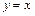Решение. Тело V ограничено снизу и сверху параболоидами вращения 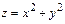, , с боков - цилиндрической поверхностью 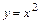, и плоскостью 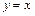(рис.2.8). Проекция этого тела на плоскость Oxy есть область, ограниченная линиями 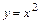, , 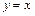(0£ x £1).
Имеем
