Эти формулы связывают интеграл по фигуре с некоторым интегралом по границе данной фигуры.
Пусть функции 
непрерывны в области D Ì Oxy и на ее границе Г; область D – связная; Г – кусочно-гладкая кривая. Тогда верна формула Грина:
; (2.22)
здесь слева стоит криволинейный интеграл I рода, справа – двойной интеграл; контур Г обходится против часовой стрелки.
Пусть Т – кусочно-гладкая ограниченная двусторонняя поверхность с кусочно-гладкой границей Г. Если функции P (x, y, z), Q (x, y, z), R (x, y, z) и их частные производные I порядка непрерывны в точках поверхности Т и границы Г, то имеет место формула Стокса:
(2.23)
слева стоит криволинейный интеграл II рода; справа – поверхностный интеграл II рода, взятый по той стороне поверхности Т, которая остается слева при обходе кривой Г.
Если связная область W Ì Oxyz ограничена кусочно-гладкой, замкнутой поверхностью Т, а функции P (x, y, z), Q (x, y, z), R (x, y, z) и их частные производные первого порядка непрерывны в точках из W и Т, то имеет место формула Остроградского-Гаусса:
(2.24)
слева – поверхностный интеграл II рода по внешней стороне поверхности Т; справа – тройной интеграл по области W.
Пример 1. Вычислить работу силы 
при обходе точки ее приложения окружности Г: 
, начиная от оси Ox, по часовой стрелке (рис. 2.18).
Решение. Работа равна 
. Применим формулу Грина (2.22), ставя знак “-” справа перед интегралом (так как обход контура – по часовой стрелке) и учитывая, что P (x, y)= x - y, Q (x, y)= x + y. Имеем:
,
где SD – площадь круга D: 
, равная 
. В итоге: 
– искомая работа силы.
Пример 2. Вычислить интеграл 
, если Г есть окружность 
в плоскости z =2, обходимая против часовой стрелки.
Решение. По формуле Стокса (2.23) исходный интеграл сведем к поверхностному интегралу по кругу Т:
T: 
Итак, учитывая, что 
, имеем:
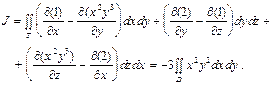
Последний интеграл есть двойной интеграл по кругу D Ì Oxy, на который проектировался круг Т; D: 
. Перейдем к полярным координатам: x = r cosj, y = r sinj, jÎ[0;2p], r Î[0;1]. В итоге:
.
Пример 3. Найти поток П векторного поля 
через полную поверхность Т пирамиды W: 
(рис. 2.19) в направлении внешней нормали к поверхности.
Решение. Поток равен 
. Применяя формулу Остроградского-Гаусса (2.24), сводим задачу к вычислению тройного интеграла по фигуре W -пирамиде:
Пример 4. Найти поток П векторного поля 
через полную поверхность T пирамиды W: 
; 
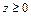(рис. 2.20), в направлении внешней нормали к поверхности.
Рис. 2.20
Решение. Применим формулу Остроградского-Гаусса (2.24)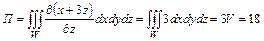 
, где V – объем пирамиды. Сравним с решением непосредственного вычисления потока (
– грани пирамиды).
,
так как проекция граней 
на плоскость Oxy имеет нулевую площадь (рис. 2.21),
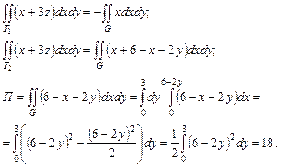
Рис. 2.21
ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
