Цель работы. Используя пространственную выборку таблицы 4.1 и команду Поиск решения, построитьнелинейную множественную регрессию для производственная функция Кобба-Дугласа.
Таблица 4.2
| ||||||
| ||||||
|
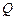
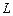
Производственная функция Кобба-Дугласа имеет вид:
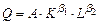, (4.1)
где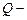 
объем производства, 
затраты капитала, затраты труда. Показатели 
являются коэффициентами частной эластичности производства 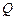соответственно по затратам капитала и труда 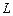. Это означает, что при увеличении одних только затрат капитала (труда) на 1% объем производства увеличивается на 
% (
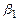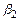%). При этом имеет место ограничение 
.
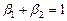Решение. Нахождение оценок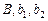 
для коэффициентов 
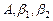нелинейной модели (4.1) будем осуществлять из решения следующей задачи условной минимизации:
(4.2)
при ограничении
. (4.3)
Для решения этой задачи используем команду Поиск решения. Первоначально введем в столбцы A,B,C значения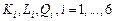 
(см. рис. 4.1). Затем в ячейках В10, В11, В11 зададим начальные («стартовые») значения искомых коэффициентов: 
.
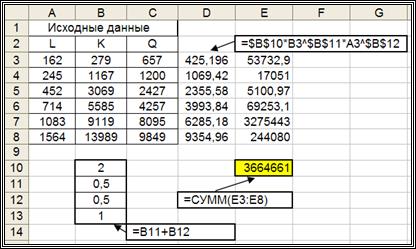
Рис. 4.1. Подготовительные вычисления
для решения задачи условной минимизации
После этого в соответствующих ячейках столбца D вычислим значения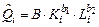 
. В столбце Е запрограммируем вычисления значений 
, а в ячейке Е10 (выделена цветом) вычислим значения функционала
. (4.4)
После этих подготовительных вычислений для выполнения команды «Поиск решения» необходимо обратиться к пункту основного меню Сервис и в появившемся меню щелкнуть мышью на команде Поиск решения. Затем в появившемся диалоговом окне выполнить следующие действия (см. рис. 4.2):
Рис. 4.2. Задание параметров команды Поиск решения
· в поле ввода Установить целевую ячейку ввести адрес ячейки, в которой вычисляется значение минимизируемого функционала (в нашем примере – Е10);
· включить опцию Минимальное значение (ищутся значения коэффициентов, при которых функционал достигает своего минимального значения);
· в поле ввода Изменяя значения ввести адреса ячеек, в которых находятся значения искомых коэффициентов (в нашем примере это ячейки В10:В12);
· щелкнув мышью на кнопке Добавить формируем ограничения на значения искомых коэффициентов (в нашем примере это условие (4.3)).
После задания параметров щелкаем на кнопке Выполнить и в ячейках В10, В11, В12 выводятся вычисленные значения коэффициентов, а в ячейке Е10 – значение функционала (4.4) при этих значениях коэффициентов (см. рис. 4.3). Видно, что вычисленные значения коэффициентов 
, 
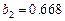удовлетворяют ограничению (4.3)
Таким образом получено следующее уравнение регрессии:
Контрольная работа № 1
Парная регрессия
Данные, характеризующие прибыль торговой компании «Все для себя» за первые 10 месяцев 2005 года (в тыс. руб.), даны в следующей таблице:
Таблица К1
| январь | февраль | март | апрель | май |
| 382 + N | 402 + N | 432+ N | 396+ N | 454+ N |
| июнь | июль | август | сентябрь | октябрь |
| 419+ N | 460+ N | 447+ N | 464+ N | 498+ N |
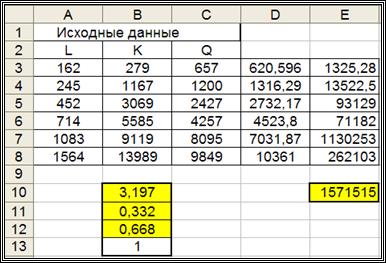
Рис. 3.9. Результаты работы команды Поиск решения
В этой таблице 
две последних цифры номера зачетной книжки студента.
Требуется:
1. Построить диаграмму рассеяния.
2. Убедится в наличии тенденции (тренда) в заданных значениях прибыли фирмы и возможности принятия гипотезы о линейном тренде.
3. Построить линейную парную регрессию (регрессию вида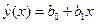 
). Вычисление коэффициентов 
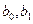выполнить методом наименьших квадратов.
4. Нанести график регрессии на диаграмму рассеяния.
5. Вычислить значения статистики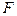 
и коэффициента детерминации 
. Проверить гипотезу о значимости линейной регрессии.
6. Вычислить выборочный коэффициент корреляции и проверить гипотезу о ненулевом его значении.
7. Вычислить оценку дисперсии случайной составляющей эконометрической модели.
8. Проверить гипотезы о ненулевых значениях коэффициентов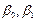 
.
9. Построить доверительные интервалы для коэффициентов 
.
10. Построить доверительные интервалы для дисперсии случайной составляющей эконометрической модели.
11. Построить доверительную область для условного математического ожидания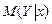 
(диапазон по оси январь – декабрь). Нанести границы этой области на диаграмму рассеяния.
12. С помощью линейной парной регрессии сделать прогноз величины прибыли и нанести эти значения на диаграмму рассеяния. Сопоставить эти значения с границами доверительной области для условного математического ожидания 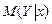и сделать вывод о точности прогнозирования с помощью построенной регрессионной модели.
Контрольная работа № 2
