Цель работы. Вычислить коэффициенты уравнения линейной регрессии по пространственной выборке таб. 1.1, используя функцииExcel.
Функции Excel. Приведем некоторые статистические функции Excel, полезные при построении парной линейной регрессии.
Функция ОТРЕЗОК. Вычисляет коэффициент 
и обращение имеет вид
ОТРЕЗОК(диапазон_значений_ 
; диапазон_значений_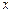 
).
Функция НАКЛОН. Вычисляет коэффициент 
и обращение имеет вид
НАКЛОН(диапазон_значений_ ; диапазон_значений_ ).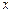
Функция ПРЕДСКАЗ. Вычисляет значение линейной парной регрессии при заданном значении независимой переменной (обозначена через 
) и обращение имеет вид
ПРЕДСКАЗ(; диапазон_значений_ ;диапазон_значений_ ).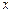
Функция СТОШYX. Вычисляет оценку 
для среднеквадратического отклонения 
возмущений 
и обращение имеет вид (YX – латинские буквы):
СТОШYX(диапазон_значений_ ; диапазон_значений_ ).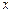
Решение. Фрагмент документа Excel, вычисляющего требуемые величины приведен на рис. 1.4. 
Обратите внимание на использовании абсолютной адресации при вычислении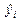 
.
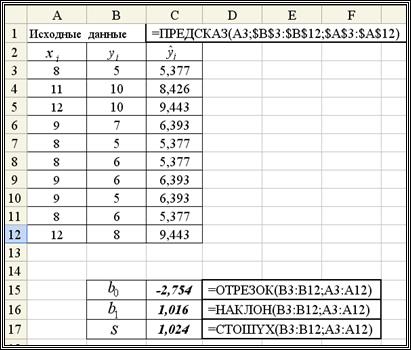
Рис. 1.4. Использование функций Excel
Задание. Сравните вычисленные значения 
с значениями, полученными в лабораторных работах №1.1 и № 1.3.
Лабораторная работа № 1.5
Построение интервальной оценки
Для функции парной линейной регрессии
Цель работы. Построение интервальной оценки для функции регрессии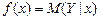 
с надежностью g = 0.95, используя для этого уравнение регрессии 
, построенное в лабораторной работе № 1.1.
Расчетные соотношения. Интервальная оценка (доверительный интервал) для 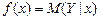(при заданном значении 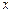) с надежностью (доверительной вероятностью) равной g определяется выражением
. (1.12)
Оценка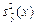 
для дисперсии функции имеет вид
, (1.13)
где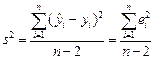 
- оценка дисперсии 
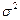. Таким образом, в (1.12) входят две величины 
(зависит от 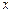) и 
, вычисляемая с помощью функции Excel:
=СТЬЮДРАСПОБР(
).
Решение. Значения нижней 
и верхней 
границ интервала (1.12) будем вычислять для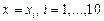 
. Фрагмент документа, осуществляющий эти вычисления, приведен на рис. 1.5.
Рис.1.5. Построение интервальной оценки для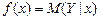
Величины 
, 
, 
(ячейки В16:В18) и коэффициенты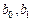 
(В1:В2) взяты из предыдущих лабораторных работ. Величина
= СТЬЮДРАСПОБР(
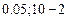) = 2.31.
Лабораторная работа № 1.6
Проверка значимости уравнения линейной регрессии
По критерию Фишера
Цель работы. По данным таблицы 1.1 оценить на уровне a = 0.05 значимость уравнения регрессии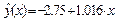 
, построенного в лабораторной работе № 1.1.
Расчетные соотношения. Уравнение парной регрессии значимо с уровнем значимости a, если выполняется следующее неравенство:
(1.14)
где F g; 1; n -2 – значения квантиля уровня g F -распределения с числами степеней свободы k 1 = 1 и k 2 = n – 2. Для вычисления квантиля можно использовать следующее выражение
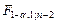= FРАСПОБР(
). (1.15)
Суммы 
, входящие в (1.14) определяются выражениями:
, 
. (1.16)
Критерий (1.14) часто называют критерием Фишера или F-критерием.
Решение. На рис. 1.6 приведен фрагмент документа Excel, вычисляющего значения Qe,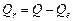 
и критерий F. В столбце D значения вычисляются по формуле 
. Значения коэффициентов 
взяты из лабораторной работы № 1.1.
Получены следующие значения 
, 
, 
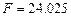. По формуле (1.15) вычисляем квантиль F 0.95; 1; 8 = 5.32. Неравенство (1.14) выполняется, т. е. 24.04 > 5.32 и поэтому уравнение регрессии 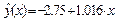значимо с уровнем значимости a = 0.05.
Рис. 1.6. Вычисление величины F – критерия
