Цель работы. Вычисление коэффициентов уравнения линейной регрессии по пространственной выборке таб. 1.1.
Расчетные соотношения. Коэффициенты, определяемые на основе метода наименьших квадратов, являются решением системы уравнений
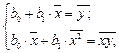(1.2)
где
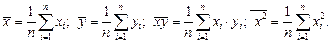(1.3)
Решая эту систему уравнений, получаем
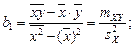(1.4)
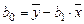, (1.5)
где mXY – выборочное значение корреляционного момента, определенного по формуле:
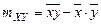, (1.6)
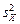– выборочное значение дисперсии величины X, определяемой по формуле:
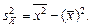(1.7)
Решение. Вычислим эти коэффициенты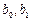 
, используя табличный процессор Excel (версия XP). На рис. 1.1 показан фрагмент документа Excel, в котором: а) размещены данные таблицы 1; б) запрограммировано вычисление коэффициентов 
, 
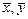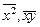системы (1.2); в) запрограммировано вычисление b 0, b 1 по формулам (1.4), (1.5) соответственно.
Заметим, что для вычисления средних значений используется функция Excel СРЗНАЧ(диапазон ячеек).
В результате выполнения запрограммированных вычислений получаем b 0 = –2.75; b 1 = 1.016, а само уравнение регрессии (1.1) примет вид
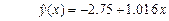. (1.8)
Задание. Используя уравнение (1.8), определите производительность труда шахтера, если толщина угольного слоя равна: а) 8.5 метров (интерполяция данных); б) 14 метров (экстраполяция данных).
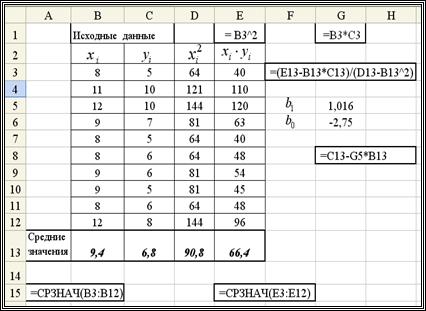
Рис. 1.1. Вычисление коэффициентов линейной регрессии
Лабораторная работа № 1.2
Вычисление выборочного коэффициента корреляции
Цель работы. Вычисление выборочного коэффициента корреляции по пространственной выборке таб. 1.1.
Расчетные соотношения. Выборочный коэффициент корреляции определяется соотношением
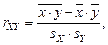(1.9)
где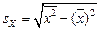 
, 
, 
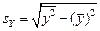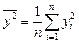. (1.10)
Решение. Фрагмент документа Excel, вычисляющего величины: коэффициента корреляции (формула (1.9));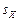 
, 
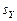(формулы (1.10), приведен на рис. 1.2.
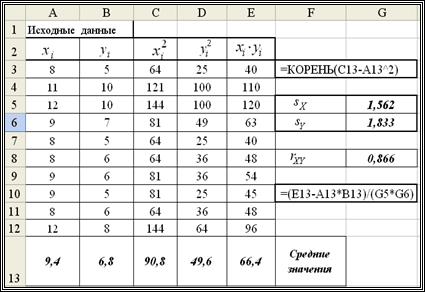
Рис. 1.2. Вычисление коэффициента корреляции
Лабораторная работа № 1.3
Вычисление оценок дисперсий коэффициентов парной линейной регрессии
Цель работы. Вычислить оценки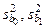 
для дисперсий коэффициентов b 0, b 1, определенных в лабораторной работе № 1.1.
Расчетные соотношения. Оценки для дисперсий коэффициентов 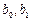определяются формулами:
, 
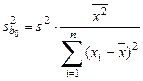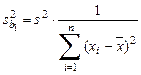(1.11)
где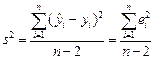 
- оценка дисперсии 
.
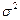Решение. На рис. 1.3 показан фрагмент документа Excel, в котором выполнены вычисления оценок дисперсий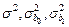 
.
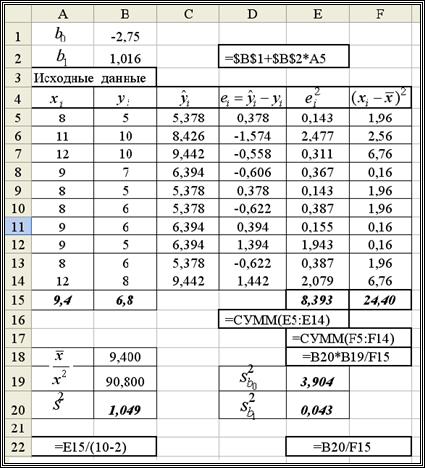Рис. 1.3. Вычисление оценок для дисперсий коэффициентов
Заметим, что
· значения коэффициентов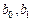 
взяты из лабораторной работы № 1.1 и ячейки (В1,В2), в которых они находятся, имеют абсолютную адресацию ($В$1, $В$2) в выражениях, вычисляющих значения регрессии 
;
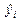· значение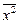 
(ячейка В19) взято из лабораторной работы № 1.1.
Получаем следующие значения: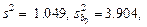 
.
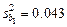Лабораторная работа № 1.4
