Цель работы. Используя пространственную выборку таблицы 3.1 необходимо вычислить вектор коэффициентов 
уравнения регрессии (3.1).
Расчетные соотношения. Вектор коэффициентов, найденный методом наименьших квадратов является решением следующей системы уравнений:
,
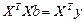где 
- матрица размера 
, первый столбец которой составлен из 1, а другие два столбца составлены из значений 
,т.е. матрица имеет следующую структуру (символы … означают не отображенные элементы)
,
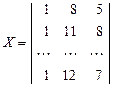а 
- вектор, составленный из 10 значений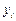 
, т.е.
.
Матрица 
имеет обратную матрицу 
и тогда вектор коэффициентов вычисляется в виде:
. (3.2)
Матричные функции Excel. Для реализации этой матричной формулы в необходимо выполнить следующие операции: транспонирование; умножение матриц (частный случай – умножение матрицы на вектор); вычисление обратной матрицы. Все эти операции можно реализовать с помощью следующих матричных функций Exce l. Для работы с этими функциями можно или а) обратиться к Мастеру функций и выбрать нужную категорию функций, затем указать имя функции и задать соответствующие диапазоны ячеек, или б) ввести с клавиатуры имя функции задать соответствующие диапазоны ячеек.
Транспонирование матрицы осуществляется с помощью функции ТРАНСП (категория функций – Ссылки и массивы). Обращение к функции имеет вид:
ТРАНСП (диапазон ячеек),
где параметр диапазон ячеек задает все элементы транспонируемой матрицы (или вектора).
Умножение матриц осуществляется с помощью функции МУМНОЖ (категория функций – Математические).Обращение к функции имеет вид:
МУМНОЖ(диапазон_1;диапазон_2),
где параметр диапазон_1 задает элементы первой из перемножаемых матриц, а параметр диапазон_2 – элементы второй матрицы. При этом перемножаемые матрицы должны иметь соответствующие размеры (если первая матрица 
, вторая -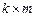 
, то результатом будет матрица 
).
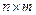Обращение матрицы (вычисление обратной матрицы) осуществляется с помощью функции МОБР (категория функций – Математические). Обращение к функции имеет вид:
МОБР (диапазон ячеек),
где параметр диапазон ячеек задает все элементы обращаемой матрицы, которая должна быть квадратной и невырожденной.
При использовании этих функций необходимо соблюдать следующий порядок действий:
· выделить фрагмент ячеек, в которые будет занесен результат выполнения матричных функций (при этом надо учитывать размеры исходных матриц);
· ввести арифметическое выражение, содержащее обращение к матричным функциям Excel;
· одновременно нажать клавиши [Ctrl], [Shift], [Enter]. Если этого не сделать, то вычислится только один элемент результирующей матрицы или вектора.
Решение. Сформируем матрицу и вектор (см. рис. 3.1).
Рис. 3.1. Вычисление коэффициентов множественной регрессии
Затем выполним формирование матрицы 
, вектора 
и вычисление вектора 
по формуле (3.2). Все эти вычисления показаны на рис. 3.1.
Получен вектор коэффициентов 
и тогда уравнение регрессии (3.1) примет вид:
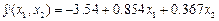. (3.3)
Лабораторная работа № 3.2
