Лекція 4. Ускладнення математичних об’єктів. Розширення уявле­нь про відношення

У даній лекції будуть розглянуті частковий випадок відношення часткового порядку, що призводить до важливого поняття решітки, і замикання відношень.

1. Решітки. Розпочнемо з фундаментального поняття решітки.

Визначення. Решіткоюназвемо частково впорядковану множину, кожні два элементи a,b якої мають нижню (позначимо через a È b) і верхню (позначимо через a Ç b) грані.

 

 

а) б) в) г)

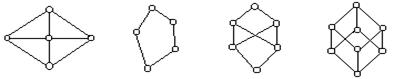
Рис.11. Приклади діаграм частково впорядкованих множин.

На рис. 11 зображені діаграми чотирьох частково впорядкованих множин. Перші два з них становлять важливі приклади решіток; четверте – також решітка. Третя множина не є решіткою.

Замикання відношень. Поняття замикання є фундаментальним математичним по­нят­тям і використовується в більшості розділів математики. Щоб продемонструвати це поняття, розглянемо наступний приклад.

Візьмемо об’єкт x₀ і процес p, який породжує множину і визначає послідовність x₁, x₂,..., x_n, ... таку, що

x₁ Î p( x₀ ),

x₂ Î p( x₁ ),

...

x_n Î p( x_n-1 ),

...

Множина, що містить всі елементи всіх послідовностей, які можуть бути виділені за допомогою р, і що починаються з x₀, називається замиканням процесу р відносно x₀. Тому “відповідь” буде міститись в р (x_n) при певному n. Однак ми не знаємо завчасно значення n. Більш того, якщо ми візьмемо випадковий елемент y з цього замикання і виконаємо процес р, починаючи з y, то не отримаємо нічого нового. Результат вже міститься в замиканні. Множина не може бути розширеною таким шляхом (вона замкнена).

Приклад. Візьмемо квадрат S, розмічений, як це показано на рис.12, і визначимо процес r наступним чином. З заданого положения S процес r породжує множину всіх поло­жень, що отримаються в результаті повороту квадрата за годинниковою стрілкою на прямий кут.

А В D A

 

D C C B

Рис. 12 Рис. 13

 

Таким чином, r( S) дає кофігурацію, зображену на рис.13. Після застосування r чотири рази, ми повернемося до положення, з котрого розпочали процес, і, отже, замикання в да­ному випадку є множина з чотирьох позицій.

A B D A C D B C

 

,,,.

 

D C C B B A A D

Розглянемо тепер, що відбудеться, якщо процес визначити за допомогою відношення. (В дійсності, це завжди можливо, що ми можемо визначити потрібне відношення за допо­могою множини {(x, y): y Î p (x), де р – досліджуваний процес}).

Для побудови замикання відношення a на множині R попередньо введемо поняття n-го ступеня відношення a. Саме шляхом звичайного теоретико-множинного комбі­нування ступенів відношення a можна отримати замикання відношення a на множині R.

Визначення. n-им ступінь відношення a на множині R (позначається aⁿ) визначається наступним чином:

1) r_i a¹ r_j тоді і тільки тоді, коли r_i a r_j;

2) r_i aⁿ r_j для n > 1 тоді і тільки тоді, коли існує такий елемент r_t множини R, що r_i a r_t і r_t a^n-1 r_j.

Визначення. Транзетивним замиканням (чи просто замиканням) відношення a на множині R називається нескінченне об’єднання

Тран­зи­тивне замикання відношення a на множині R позначають a⁺.

Можна також визначити транзитивне замикання таким чином: r_i a⁺ r_j тоді і тільки тоді, коли r_i aⁿ r_j для деякого n ³ 1. Або r_i a⁺ r_j, якщо існує така послідовність r₁, r₂,...,r_k із нуля і більше елементів множини R, що r_i a r₁, r₁ a r₂,..., r_k-1 a r_k, r_k a r_j.

Транзитивність замикання відношення a на множині R є наслідком, очевидно, означення замикання.

Приклад. 1. Нехай a – відношення на множині N таке, що a = {(x, y): y = x + 1}. Тоді a⁺ = {(x, y): x < y}.

2. Нехай L – множина станцій Київского метро і a, b та c – послідовно розташовані його станції. Якщо відношення a₁ на L визначене як a₁ = {(x, y): x є наступною за у станцією}, то (a, b) і (b, c) Î a₁ і (a,a), (b,b), (c,c) і (a,c) Î a₁². Отже, a₁⁺ = L´L.

На цих прикладах видно, що замикання відношення в загальному випадку не є реф­лексивним. Однак іноді зручно зробити його таким. Це можна легко зробити. Приймемо, що еквівалентне відношення I = {(x, x) | x Î R} на множині R, є нульовим ступенем будь-якого відношення на множині R. Таким чином, a⁰ = I для будь-якого a на множині R.

Визначення. Рефлексивним замиканням відношення a множині R (позначається a*) називається множина

Можна також визначити рефлексивне замикання таким чином:

1) r_i a* r_i для всіх r_i Î R;

2) r_i a* r_j, якщо r_i a⁺ r_j;

3) в a* немає нічого іншого, крім того, що міститься там згідно з 1) і 2).

Замикання відношень пов’язані між собою очевидним співвідношенням a* = a⁺ È I.

Приклад. Використовуючи відношення a, визначене в попередньому прикладі, отримуємо a* = {(x,y): x £ y).