Визначення. Якщо ліва композиція g○f функцій f: S → T і g: T → S співпадає з тотожною функцією 1S на множині S, ми будемо говорити, що функція g – ліва обернена до функції f,а функція f – права обернена до функції g, функція f - оборотна зліва,функція g - оборотна справа. Якщо, крім того, f ○ g = 1T, ми будемо говорити, що функція g – двобічно оборотна до f і, за симетрією, функція f – двобічно оборотна до g. Функція, яка має двобічно оборотну, називається оборотною.
Теорема 2. Функція оборотна зліва тоді і тільки тоді, коли вона ін ’ єктивна. Функція оборотна справа тоді і тільки тоді, коли вона сюр’єктивна.
Доведення. Покажемо спочатку, що будь-яка оборотна зліва функція ін ’ єктивна. Нехай g: T → S – функція, обернена зліва до f:S → T. Припустимо, що f (s) = f (s'). Тоді за означенням,
s=1S(s) =g(f ( s )) = g (f (s')) = 1S(s') = s'
Таким чином, виходячи з припущення, що f (s) = f (s' ), ми встановили, що s = s'. Це доводить ін’єктивність f. Залишається перевірити обернене твердження, щоб закінчити доведення першої частини теореми: нам потрібно показати, що якщо f ін’єктивна, то для неї існує ліва обернена g 1 функція, тобто g 1 f = 1S. З цією метою виберемо елемент s1 ÎS і визначимо g 1:T → S таким чином:

Тоді (g 1 f)(s)= g 1(f (s)) = sдля всіх sÎS, так що, за означенням, g 1 f = 1S і g 1 є лівою оберненою до f.
Аналогічно перевіряється друга частина теореми. Якщо tÎT і fh = 1T, то t = 1T(t) = f (h (t)), тому що будь-який елемент tÎT є образом f (s) певного елемента s = h (t) Î S, і f сюр ’ єктивна. В інший бік, якщо f:S → T сюр ’ єктивна, то кожен елемент tÎT є образом t = f (s)хоча б одного елемента s Î S. Для кожного елемента t Î T виберемо з множини всіх s, що переходять в t, одного представника і позначимо його, скажімо, через h (t). Тоді ми отримаємо функцію h:T → S,таку, що f (h (t)) = t для всіх tÎT, тобто fh = 1T, як стверджувалось. Теорема доведена.
Наслідок. Функція f: S → T є бієкцією тоді і тільки тоді, коли вона є оборотною зліва і справа.
Теорема 3. Наведені нижче властивості функції f: S → T еквівалентні:
(i) функція f – бієкція;
(ii) функція f має ліву обернену функцію g і праву обернену функцію h.
Якщо ці властивості виконуються, то
(iii) всі обернені до f функції (ліві, праві і двобічні) співпадають. Ця єдина обернена до функції f функція f –1, бієктивна, і
(f –1) –1 = f. (2)
Доведення. Еквівалентність властивостей (i) і (ii) є просто переформулюванням попереднього наслідку. Наслідком умови (ii) є
g = g 1T = g (fh) = (gf) h = 1s h = h.
Це показує, що всі ліві і праві обернені до функції f функції співпадають, і доводить властивість (iii). Нарешті, бієктивна функція f обернена до своєї оберненої функції g = h, оскільки gf =1s і fh = 1T. Отже, обернена функція бієктивна і має функцію f своєю єдиною оберненою функцією, тобто (f –1)–1 = f.
Визначення. Квадрат будь-якої функції f: S → S визначається як функція f 2 = f ° f = f ◊ f,тобто як результат дворазового застосування функції f. Коли f 2 = f, функція f називається ідемпотентом чи проектором.
Наприклад, ортогональний проектор (x, y)-площини на x- вісь або y- вісь є ідемпотентом. Відзначимо також, що ці два проектори мають властивість f○g=g○f (чи, що те ж саме, g ◊ f = f ◊ g), оскільки f○g і g○f відібражують будь-яку точку площини у початок координат (0,0).
Визначення. Пари функцій f, g з властивістю fg=gf називаються комутуючими чи перестановочними.
Стосовно будь-якої з двух композицій ми можемо назвати функцію g ÎS2 лівою оберненою до функції f Î S2, якщо fg = 1S. Аналогічно, права обернена до f — це функція h така, що fh = 1S. Згідно теореми 2, функція f має ліву обернену функцію відносно лівої композиції, і тільки тоді, коли f є ін’єкцією. Значить, те ж відноситься до існування правої оберненої функції до f відносно правої композиції. Аналогічно, функція f має обернену справа функцію відносно лівої композиції тоді і тільки тоді, коли f - сюр’єкція.
Двобічна обернена існує в точності для бієктивних функцій незалежно від того, яку з композицій (ліву чи праву) ми розглядаємо. Функція, обернена до f, позначається через f – 1. Вона існує у тому і тільки у тому випадку, коли функція f бієктивна, і задовільняє відношенням
f – 1 f = f f – 1 = 1s (і для лівої і для правої композиції).
Деякі спеціальні класи функцій. На закінчення лекції ми коротко розглянемо такі чотири важливих класи функцій: підстановки; послідовності; функціонали і відображення, що зберігають еквівалентність. Ці функції часто використовуються, в теорії графів, теорії граматик для визначення мов програмування і перекладу, в машинній графіці.
Визначення. Підстановкою множини А називається будь-яка бієкція на А.
Підстановкискінченних множин становляють особливий інтерес для розрахунків. Коли А визначене, ми в змозі розрахувати число різних підстановок А.
Нехай |А| = n Î N. Позначимо через nPn число таких підстановок. Значення nPn легко розрахувати. Можемо розглянути задачу побудови бієкції на А як задачу заповнення ящиків, занумерованих від 1 до n, a 1,..., a n (рис.8). Порядок, в якому заповнюються ящики, не суттєвий (будь-який інший порядок можна отримати перемішуванням ящиків). Тому будемо заповнювати їх зліва направо. Перший ящик може бути заповнений n способами, тому що ми маємо вільний вибір з усієї множини А. Забираючи обраний елемент з А, отримаємо множину з n – 1
1 2 n – 1 n
| ... |
Рис. 8.
елементів. Отже, другий ящик може бути заповнений n – 1 способами, третій ящик – n – 2 способами і т.д. Продовжуючи цей процес, отримаємо, що (n - 1)-й ящик може бути заповнений двома способами, а ящик з номером n – єдиним элементом з А, що залишився. Отже, число різних підстановок з А рівне
n × (n–1) × (n - 2) ×... ×3 × 2 ×1.
Цей добуток називається факторіалом n (позначається n!). Отже, nPn = n!.
Нехай Nn підмножина перших n натуральних чисел множини N. Тому що А і Nn мають однакову кількість елементів, можна звести множину А до множини Nn. Будь-яка підстановка на Nn повинна визначати образ кожного элемента в Nn (який, звичайно, повинен бути єдиним і відрізнятися від інших). Нехай підстановка на Nn. Тоді можна визначити як множину з n пар наступним чином:
{(1, x1), (2, x2),...,(n, xn)}, де {x1,...,xn} = Nn.
Не обов’язково, звичайно, повинно бути x1 = 1 і т.д. Можна також представити так им чином:

Приклад 1. Нехай підстановка на N6:

Тоді s(1) = 5, s(2) = 6, s(3) = 3 і т.д.
Перевагою цього позначення є простота, з якою можуть бути розраховані важкі підстановки. Припустимо, що - підстановка на Nn, визначена вище, а інша підстановка на тій же самій множині. Тоді підстановка може бути записана як сукупність пар в порядку, що визначається x1, x2,...xn. Якщо дві послідовності записати одна над іншою (перша застосована підстановка повинна бути записана першою), то верхній і нижній рядки утворять результуючу підстановку.
Приклад 2. Нехай підстановка з прикладу 1 і
r 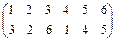
Можна переписати r у вигляді
r 
Тому r ° sможе бути розраховане наступним чином:








 r
r  однакові
однакові
 r ° s
r ° s 
Отже, наприклад, r ° s(2) = r(s(2)) = r(6) = 5 і т. д. Звідси робимо висновок, що зображення оберненої (скінченної) підстановки отримується перестановкою рядків, що зображують початкову підстановку. Хоча таке зображення краще в розрахунках, воно потребує багато зайвого місця, особливо в тих випадках, коли багато елементів не міняються в процесі підстановки. Існує більш просте позначення, котре може вживатися безпосередньо для деяких простих підстановок і опосередковано для всіх скінченних.
Визначення. Нехай А = {а1,…,аn}. Підстановку r називають циклом (циклічною підстановкою), якщо
r 
Припустимо, що А Í В і множина В проста. Розширюючи підстановку r на всі елементи В, можна визначити підстановку s так, що
 r(x), якщо х Î А,
r(x), якщо х Î А,
s: х ® x, якщо х Î В \ А.
В цьому випадку підстановка s поводить себе подібно підстановці r у всіх випадках, коли елементи В не лишаються на місці. Застосування підстановки s до А пересуває елементи по колу циклічним чином, і, якщо відома область А, ми можемо позначити підстановку як (a1, a2,…,аn). Ця підстановка називається циклом довжини n.
Приклад 3. Розглянемо знову підстановку
r 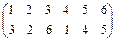
Підстановка є циклом довжини 5 і може бути записана як (1, 3, 6, 5, 4).
Не всі підстановки є циклами. Наприклад, підстановка s в прикладі 1 не є циклом. Нагадаємо, що підстановка s має вигляд

Тому s(1) = 5, s(5) = 4, s(4) = 1, звідки робимо висновок, що підстановка s містить цикл (1, 5, 4). Починаючи з 2, отримуємо інший цикл – (2, 6). Таким чином, маємо
s = (1, 5, 4) ° (2, 6) і s = (2, 6) ° (1, 5, 4).
В дійсності будь-яка скінченна підстановка може бути зображена як добуток циклів, при цьому цикли можуть міститись в будь-якому порядку. З побудови робимо висновок, що один елемент не може зустрітись більш ніж в одному циклі, тобто цикли не перетинаються.
Теорема 4. Кожна підстановка r на скінченній множині А виражається у вигляді добутку циклів, що не перетинаються.
Доведення. Оскільки | A | = n Î N, то А має таку ж кількість елементів, що й Nn. Тому без втрати загальності ми можемо обмежитись розгляданням підстановки r на Nn.У теоремі стверджується, що r = s1 ° s2 ° …° sr, де кожне si, i = 1,2,…,r, є циклом і цикли не перетинаються. Для доведення теореми наведемо потрібні цикли.
Спочатку знайдемо найменший елемент х1Î Nn такий, що r(х1) ¹ х1 і r(х) = х для всіх х, 1 £ х < х1. Якщо такого х1 не існує, то r = I (тобто r є тривіальним порожнім добутком циклів). В іншому випадку розрахуємо х1, r(х1), r2(х1), r3(х1) і т. д. Всі ці елементи знаходяться в Nn. Тому елементи в цій послідовності повинні містити повторення. Припустимо, що rk(х1) – перший такий елемент. Покажемо, що rk(х1) = х1. Припустимо, що це співвідношення не виконується. Тоді rl(х1) = rk(х1) для деякого l, 0<l<k. Отже rl-1(х1) = r-1 ° rl(х1) = r-1 ° rk(х1) = rk-1(х1) і т. д.
Тому rl-1(х1) = rk-1(х1), тобто rk-l(х1) = r0(х1) = х1, що суперечить мінімальності k (тому що k-l < k). Таким чином, rk(х1) = х1 і підстановка s1 = (х1, r(х1), r2(х1),…,rk-1(х1)) задає цикл всередині r.
Якщо всі елементи х Î N n такі, що r(х) ¹ х (будемо називати такі елементи нестаціонарними), містяться в s1, то r = s1 – єдиний цикл (який не перетинаєтся). В іншому випадку знайдемо наступний найменший елемент х2 Î N n такий, що r(х2) ¹ х2 і х2 не зустрічається в s1. З х2 будуємо множину різних ступенів r: s2 = (х2, r(х2), r2(х2),…, rm(х2)). Це цикл довжини не менше 2 і він не перетинаєтся з s1.
Якщо всі нестацівонарні елементи вичерпані, то r = s1 ° s2 = s2 ° s1. Очевидно, що множину нестаціонарних елементів, що не входять в ці цикли, можна зменшити, і в кінці кінців ми прийдемо до Æ. Отже, r = s1 ° s2 ° s3°… ° sr для деякого r Î N.
Розглянемо тепер ситуацію з множинами А: |A| = n і B Í A, |B| = r £ n, взявши за проблему визначити число бієктивних функцій з А в В чи, що еквівалентно, число ін’єктивних відображень з В в А.
Число перестановок (без повторів) з n елементів по r позначається nPr і розраховується так же, як і nPn, за винятком того факту, що процес припиняється після заповнення r ящиків. Таким чином,
nPr = n×(n–1)×…×(n–r+1).
Легко бачити, що, продовжуючи процес заповнення ящиків, n – rелементів, що залишилися, можна розмістити по останнім n – rящикам n-rPn-r способами. Тому і
nPr = (nPn)/ (n-rPn-r) = n! / (n–r)!
При розрахунку nPr ми знаходимо число бієктивних функцій з А в В. Підрахуємо число таких функцій.
Визначення. Нехай А – скінченна множина і B Í A, |А| = n ³ r = |B |. Множина В називається з’єднанням (без повторів) з n елементів по r. Число таких з’єднань позначається Сrn.
Розрахунок Сrn відбувається наступним чином. Покладемо |A| = n. Візьмемо випадкову підмножину B Í Aтаку, що |В| = r. Тоді В є шляхом підстановки з n елементів по r. Число ін’єктивних функцій на А, що мають B своим шляхом, є nPr. Якщо f є такою функцією і g –інша така функція, яка має ту ж саму область значень, то g пов’язане з f спввідношенням g = j°f, де j – підстановка на В.
Функції g і f визначають одну і ту ж комбінацію, і в дійсності число функцій, що визначають цю комбінацію, рівне числу підстановок j на B. Отже, nPr = Сrn× rPr, звідки Сrn = (nPr)/(rPr) = n!/r!×(n–r)!
Оскільки відносні доповнення єдині і | A \ B | = n – r, то звідси робимо висновок, що Сrn= Сn–rn.
Розглянемо як функції деякі відомі матаматичні об’єкти.
Визначення. Послідовністю на множині S називається всюду визначена функція N ® Z.
Якщо s: N ® Z– задана послідовність і s(n) = sn, то звичайно позначають послідовність не s, а (sn) чи (s1,s2,…,sn,…). В цьому випадку sn називають n-м членом послідовності.
Особливий інтерес в задачах, пов’язаних з трансляцією мов програмування, становлять функціонали. Іх особливість полягає в тому, що їх значення належать множині функцій.
Визначення. Нехай дані множини А, В і C. Позначимо через [ В ® C ] множину всіх функцій з множини В в множину C. Функція F: А ®[ B ® C ] називається функціоналом.
Приклад 4.Нехай Р – множина програм, тобто текстів програм, які повинні бути оброблені компілятором. Аналогічно нехай I і О – множини відповідно вихідних і вхідних значень, які доступні програмі для вводу і виводу. Тоді компілятор (з відповідної мови) є функціоналом типу P ®[ I ® O ]; для даної р Î Р він намагається створити машинний код, який при виконанні буде читати i Î I і видавати оÎ О.
Приклад 5.Нехай всі дані належать R. Тоді якщо f: a®[x®a + x], то f(2): x®2 + x і f(2)(3) = 5, тоді як f(3): x®3 + x і f(3)(3) = 6 і т. д.
Будемо розглядати функціонали просто як функції, що мають нетривіальні області значень і будемо поводитись з ними відповідним чином.
На завершення визначимо функції, які зберігають певні структури. Спочатку знову розглянемо відоме нам співвідношення відношення еквівалентності і розбиття.
Визначення. Нехай Х – множина, на якїй задано відношення еквівалентності r. Тоді Х розбивається відношенням r на r -еквівалентні класи; множина r-еквівалентних класів на Х позначається Х/r.
Визначення. Нехай Х і Y – множини, rх і ry – відношення еквівалентності на них і f: Х®Y – всюду визначена функція. Позначимо через`f відношення`f: X/rх ® Y/ry таке, що`f ={([x], [f(x)]): x Í X}, де [x] – клас еквівалентності х. Якщо`f – функція то х1rхх2 Þ`f([х1]) =`f([х2]) і f є відображенням, що зберігає еквівалентність. В цьому випадку говорять, що f: X ® Y індукує відображення `f: X/rх ® Y/ry.
Наочний спосіб зображення такого відображення наведено на рис. 9.
Якщо розглянути відображення f, погоджене з відношенням еквівалентності, то можна переходить від х1 до у1 чи через х2, використовуючи співвідношення y2 = f(х2) і х1rхх2, чи через y2, використовуючи співвідношення y1 = f(х1) і y2rхy1.
Приклад 6.Нехай Х = {1, 2, 3}, Y = {1, 4, 9} і rх і ry такі, що X/rх = {{1},{2,3}}, Y/ry = {{1},{4,9}}, і f: X ® Y таке, що х ® х2. Тоді
`f([1]) = [f(1)] = [1] = {1},
`f([2]) = [4] = {4, 9},
`f([3]) = [9] = {4, 9}.
В цьому випадку {2,3} Î X/rх Þ 2rх3 Þ [2] = [3] і `f ([2]) =`f([3]). Тому `f є функцією і f зберігає відношення еквівалентності.
Приклад 7.Нехай Х, Y і f є ті ж, що і в прикладі 6, і відношення еквівалентності s x і sy індукують розбиття {{1},{2,3}} і {{1,4},{9}} відповідно. В цьому випадку індуковані відношення дають
`f([2]) = [f(2)] = [4] = {1,4},
`f([3]) = [f(3)] = [9] = {9}.
Через те, що 2sх3, то [2] = [3] в X/sх , але (4, 9) Ï sr, оскільки [4] ¹ [9] в Y/s r. В порівнянні з рис.9 цей приклад дає відношення, зображені на рис.10. Через те, що не можна з’єднати сторони прямокутника у всіх випадках, то відношення еквівалентності не зберігаються.
rx sх


 x1 x2 2 3
x1 x2 2 3

 f f sх
f f sх

 f sr f
f sr f
 y1 y2 4
y1 y2 4
 ry 4 sr 9
ry 4 sr 9
рис. 9 рис 10






