Тербелмелі қозғалыстар. Табиғатта өте жиі кездесетін қозғалыстардың қатарына тербелістерді жатқызуға болады. Тербелмелі қозғалыс немесе жай тербеліс деп уақыттың өтуіне байланысты қайталанып отыратын қозғалыстарды айтады. Тербелістің түрі сан алуан болғанымен, олардың барлығы да жалпы заңдылықпен өзгереді. Олардың ең қарапайым түрі гармониялық тербелістер. Синус немесе косинус заңы бойынша уақытқа тәуелді өзгеретін тербелісті гармониялық тербеліс дейді. Ол келесі формуламен өрнектеледі:
 (8.1)
(8.1)
мұндағы 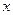 -тербеліп тұрған дененің (жүйенің) ығысуы, А – жүйенің тепе – теңдік күйден ең үлкен ауытқуы тербеліс амплитудасы,
-тербеліп тұрған дененің (жүйенің) ығысуы, А – жүйенің тепе – теңдік күйден ең үлкен ауытқуы тербеліс амплитудасы,  -
-  уақыт мезетіндегі тербеліс фазасы,
уақыт мезетіндегі тербеліс фазасы, 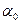 - бастапқы фазасы деп аталады. Фаза радиан немесе градус бірліктерінде өлшенеді,
- бастапқы фазасы деп аталады. Фаза радиан немесе градус бірліктерінде өлшенеді,  - циклдік жиілік, ол Т (бір период) уақыт ішіндегі болатын толық тербеліс санына тең шама.
- циклдік жиілік, ол Т (бір период) уақыт ішіндегі болатын толық тербеліс санына тең шама.
Уақыт өткен сайын жүйенің қозғалысы дәл қайталанып отырса, онда мұндай тербелісті периодтық деп атайды. Толық бір тербеліске кететін уақыт период (Т) деп аталады. Тербелуші жүйеге үйкеліс күштері әсер етпесе, онда ол еркін тербеледі, оның амплитудасы, периоды өзгермейді. Егер жүйе  уақыт ішінде
уақыт ішінде  рет тербелсе, онда
рет тербелсе, онда  ішінде
ішінде  тербеліс жасайды, ал мұны тербеліс жиілігі деп атайды, ол периодқа кері шама
тербеліс жасайды, ал мұны тербеліс жиілігі деп атайды, ол периодқа кері шама
 (8.2)
(8.2)
Период пен циклдік жиілік арасындағы байланыс
 (8.3)
(8.3)
Жиілік  өлшенеді. Бір секундта бір тербеліс жасалатын болса, онда тербеліс жиілігі берге тең, оның өлшем бірлігі герц (Гц) деп аталады.
өлшенеді. Бір секундта бір тербеліс жасалатын болса, онда тербеліс жиілігі берге тең, оның өлшем бірлігі герц (Гц) деп аталады.
Тербелмелі қозғалыс тек 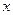 пен ғана емес, сонымен бірге жылдамдық
пен ғана емес, сонымен бірге жылдамдық  және үдеумен
және үдеумен 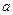 сипатталады. Олардың мәндері (8.1) өрнегінен анықталады. (8.1) өрнегін уақыт арқылы дифференциалдап жылдамдық теңдеуін аламыз:
сипатталады. Олардың мәндері (8.1) өрнегінен анықталады. (8.1) өрнегін уақыт арқылы дифференциалдап жылдамдық теңдеуін аламыз:
 (8.4)
(8.4)
(8.4) өрнегі бойынша жылдамдық та гармониялық заңға бағынады,  -- жылдамдық амплитудасы. (8.1) мен (8.4) өрнекетрін салыстырсақ, жылдамдық ығысудан фаза бойынша
-- жылдамдық амплитудасы. (8.1) мен (8.4) өрнекетрін салыстырсақ, жылдамдық ығысудан фаза бойынша  - ге озып отырады. (8.4) тағы да уақыт бойынша дифференциалдап, үдеу өрнегін табамыз:
- ге озып отырады. (8.4) тағы да уақыт бойынша дифференциалдап, үдеу өрнегін табамыз:

 (8.5)
(8.5)
(8.5) мен (8.3)-ді салыстырсақ, онда үдеу мен ығысу қарама-қарсы фазада болатындығы шығады, яғни жылдамдық өзінің ең үлкен оң мәніне жеткенде, үдеу өзінің ең үлкен теріс мәніне жетеді және керісінше болады.
Гармониялық тербелістерді векторлық диаграмма жәрдемімен көрсету. Гармониялық тербелістерді сипаттайтын  теңдеуін айналушы векторлық амплитуда көмегімен көрсетуге болады, осындай әдіспен алынған кестені векторлық диаграмма деп атайды. Алынған осьті
теңдеуін айналушы векторлық амплитуда көмегімен көрсетуге болады, осындай әдіспен алынған кестені векторлық диаграмма деп атайды. Алынған осьті 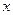 әрпімен белгілейік (8.1-сурет)
әрпімен белгілейік (8.1-сурет)


Осьтен алынған  нүктесінің осьпен
нүктесінің осьпен 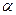 бұрышын жасайтын, ұзындығы А – амплитудаға тең векторын салайық. Егер бұл векторды сағат тілінің бағытына қарама-қарсы бағытта
бұрышын жасайтын, ұзындығы А – амплитудаға тең векторын салайық. Егер бұл векторды сағат тілінің бағытына қарама-қарсы бағытта  бұрыштық жылдамдықпен айналдырсақ, онда бұл вектордың ұшының проекциясы
бұрыштық жылдамдықпен айналдырсақ, онда бұл вектордың ұшының проекциясы 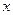 осі бойынша +А -дан –А -ға дейін өзгеріп отырады. Бұл вектордың өзгеруі гармониялық тербеліс заңдылығына бағынады, оның бұрыштық жылдамдығы циклдік жиілігіне тең, ал
осі бойынша +А -дан –А -ға дейін өзгеріп отырады. Бұл вектордың өзгеруі гармониялық тербеліс заңдылығына бағынады, оның бұрыштық жылдамдығы циклдік жиілігіне тең, ал 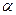 бұрышын бастапқы фаза деп қабылдауға болады. Гармониялық тербелістердегі векторлық диаграмма әдісі тербелістерді қосу кезінде кең қолданылады.
бұрышын бастапқы фаза деп қабылдауға болады. Гармониялық тербелістердегі векторлық диаграмма әдісі тербелістерді қосу кезінде кең қолданылады.
Бір бағыттағы және бірдей гармониялық тербелістерді қосу. Бірдей бағыттардағы және бірдей жиіліктердегі екі гармониялық тербелістерді қосуды қарастырайық. Тербелуші дененің 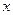 ығысуы келесі түрде жазылатын
ығысуы келесі түрде жазылатын  және
және  ығысулардың қосындысына тең болады:
ығысулардың қосындысына тең болады:

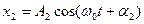 (8.6)
(8.6)
Осы екі тербелісті диаграммада  және
және 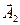 векторларының көмегімен көрсетейік (8.2-сурет)
векторларының көмегімен көрсетейік (8.2-сурет)


Қорытқы  векторын векторларды қосу ережесі бойынша анықтаймыз. Сонда бұл вектордың
векторын векторларды қосу ережесі бойынша анықтаймыз. Сонда бұл вектордың 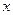 осіндегі проекциясы қосылған векторлардың проекцияларының
осіндегі проекциясы қосылған векторлардың проекцияларының  және
және  қосындысына тең екендігі суреттен оңай көрінеді:
қосындысына тең екендігі суреттен оңай көрінеді:  . Сондықтан,
. Сондықтан,  векторы қорытқы тербеліс болып табылады. Бұл вектор
векторы қорытқы тербеліс болып табылады. Бұл вектор  және
және 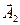 векторлары сияқты
векторлары сияқты  бұрыштық жылдамдықпен айналады, олай болса қорытқы вектор сипатталатын өрнек
бұрыштық жылдамдықпен айналады, олай болса қорытқы вектор сипатталатын өрнек  , түрде болады, мұндағы А –қорытқы тербелістің амплитудасы, ал
, түрде болады, мұндағы А –қорытқы тербелістің амплитудасы, ал 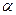 -оның бастапқы фазасы. 8.2. – суреттен А амплитудасының квадраты мынаған тең:
-оның бастапқы фазасы. 8.2. – суреттен А амплитудасының квадраты мынаған тең:
 (8.7)
(8.7)
ал бастапқы фаза төмендегі теңдеу арқылы анықталады

(8.7) өрнегінен, қорытқы тербелістің амплитудасы қосылған тербелістердің  бастапқы фазаларының айырылымына тәуелді екені шығады. Дербес жағдайларды қарстырайық:
бастапқы фазаларының айырылымына тәуелді екені шығады. Дербес жағдайларды қарстырайық:
1. Фаза айырымы  ноль немесе
ноль немесе  -ге еселенген болсын.
-ге еселенген болсын.  , онда
, онда  және
және  , яғни қорытқы тербелістің амплитудасы
, яғни қорытқы тербелістің амплитудасы  мен
мен  -нің қосындысына тең.
-нің қосындысына тең.
2. Қосылған тербелістердің  фаза айырымы
фаза айырымы  -дің тақ санына тең
-дің тақ санына тең  , онда
, онда  и
и  , яғни қорытқы тербелістің амплитудасы
, яғни қорытқы тербелістің амплитудасы  мен
мен  -нің айырымына тең.
-нің айырымына тең.
Өзара перпендикуляр тербелістерді қосу. Өзара перпендикуляр бағыттардағы тербелістерді қосуды қарастырайық (8.3-сурет). Олардың дөңгелектік (циклдік) жиіліктері және фазалары бірдей, ал амплитудалары әртүрлі болсын:
 ,
,  .
.
Екінші теңдеуді біріншіге бөлгеннен кейін  (8.8)
(8.8)
8.3-сурет болады, яғни (8.8) өрнегі, осындай екі тербелістерді қосу нәтижесінде алынған қорытқы тербеліс түзу бойымен жасалады және оның 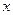 осіне көлбеулік бұрышы
осіне көлбеулік бұрышы 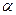 мына өрнекпен анықталады:
мына өрнекпен анықталады:
 (8.9)
(8.9)
ал осы түзу бойлап ығысу
 (8.10)
(8.10)
Бұл тербелісті сызықты – поляризацияланған деп атайды.


Егер екі тербеліс арасындағы фазалар айырымы  -ге тең болса қосылатын тербелістерді мынадай түрде жазуға болады
-ге тең болса қосылатын тербелістерді мынадай түрде жазуға болады 
 (8.11)
(8.11)
Оларды мынадай түрге келтіруге болады
 ,
,  (8.12)
(8.12)
Егер теңдеулерді квадраттап, қосатын болсақ, онда
 (8.13)
(8.13)


(8.13) өрнегі – эллипс теңдеуі, яғни нүкте қозғалысы эллипстік траектория бойынша болады (8.4-сурет). Келтірілген жағдайда эллипс бойынша қозғалыс сағат тілі бағытымен болады.  болған жағдайда (8.13) теңдеуі шеңбер теңдеуіне айналады:
болған жағдайда (8.13) теңдеуі шеңбер теңдеуіне айналады:  (8.14)
(8.14)
Серіппелі, физикалық және математикалық маятниктер. Серпімді күштің әсерінен болатын тербелістерді, мысалы серіппелі маятниктің тербелісін қарастырайық. Серіппелі маятник ретінде абсолют серпімді серіппеге ілінген массасы 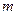 жүкті алуға болады.
жүкті алуға болады.  серпімді күштің әсерінен серіппелі маятник гармоникалық тербеліс жасайды. Серпімділік коэффициент
серпімді күштің әсерінен серіппелі маятник гармоникалық тербеліс жасайды. Серпімділік коэффициент  берілген жағдайда қаттылық деп аталады.
берілген жағдайда қаттылық деп аталады.
Тепе-теңдік күйден шығарылған тербелістегі жүйеге сырттан ешқандай әсер болмаған кездегі жүйенің онан арғы тербелісі еркін тербеліс деп аталады. Ньютонның екінші заңына серпімді (немесе квазисерпімді) күш үшін өрнекті қойсақ:
 (8.15)
(8.15)
немесе  (8.16)
(8.16)
мұндағы  ,
,  ,
,  -тербелмелі жүйенің меншікті жиілігі деп аталатын шама. Сонымен, үйкеліс күші болмаған кезде, серпімді (немесе квазисерпімді) күш әсерінен болатын қозғалыс (8.16) дифференциалды теңдеуімен сипатталады, оның шешімі
-тербелмелі жүйенің меншікті жиілігі деп аталатын шама. Сонымен, үйкеліс күші болмаған кезде, серпімді (немесе квазисерпімді) күш әсерінен болатын қозғалыс (8.16) дифференциалды теңдеуімен сипатталады, оның шешімі
 (8.17)
(8.17)
Олай болса,  түріндегі күш әсерінде тұрған жүйе қозғалысы гармоникалық тенрбеліс болып табылады. Серіппелі маятниктің тербеліс периоды
түріндегі күш әсерінде тұрған жүйе қозғалысы гармоникалық тенрбеліс болып табылады. Серіппелі маятниктің тербеліс периоды
 (8.18)
(8.18)
Бұл өрнек, серіппе массасы дене массасымен салыстырғанда аз болған кезде орынды.
Квазисерпімді күштерді әсерінен (серпімді күштерден табиғаты бөлек, бірақ ығысуға пропорционал, яғни  шартын қанағаттандыратын күш) гармониялық тербеліс жасайтын денелерге физикалық және математикалық маятниктер жатады. Бұл маятниктер өте маңызды практикалық мәнге ие.
шартын қанағаттандыратын күш) гармониялық тербеліс жасайтын денелерге физикалық және математикалық маятниктер жатады. Бұл маятниктер өте маңызды практикалық мәнге ие.
Физикалық маятник деп оның  ауырлық ценрі арқылы өтпейтін кез-келген нүктесі арқылы
ауырлық ценрі арқылы өтпейтін кез-келген нүктесі арқылы  осінің төңірегінде тербеліске келетін қатты денені айтамыз (8.5-сурет).
осінің төңірегінде тербеліске келетін қатты денені айтамыз (8.5-сурет).  -ға тең
-ға тең  қашықтығы физикалық маятниктің ұзындығы деп аталады. Маятникті тепе-теңдік қалпынан
қашықтығы физикалық маятниктің ұзындығы деп аталады. Маятникті тепе-теңдік қалпынан 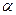 бұрышқа бұрған кезде, маятникті алғашқы қалыпқа алып келуге тырысатын айналдырушы момент пайда болады.
бұрышқа бұрған кезде, маятникті алғашқы қалыпқа алып келуге тырысатын айналдырушы момент пайда болады.  күшінің айналдырушы моменті
күшінің айналдырушы моменті
 (8.19)
(8.19)
Шексіз аз бұрыш кезінде  екенін ескеріп, момент
екенін ескеріп, момент  болады. Маятниктің айналу бұрышының уақытқа тәуелділігін алу үшін, қозғалмайтын оське қатысты айналатын дене динамикасының негізгі заңын пайдаланамыз:
болады. Маятниктің айналу бұрышының уақытқа тәуелділігін алу үшін, қозғалмайтын оське қатысты айналатын дене динамикасының негізгі заңын пайдаланамыз:
 (8.20)
(8.20)
(8.19) және (8.20) теңдеулерді теңестіріп, келесі өрнекті аламыз:


8.5-сурет
 (8.21)
(8.21)
немесе

мұндағы  осіне қатысты маятниктің инерция моменті,
осіне қатысты маятниктің инерция моменті,  - бұрыштық үдеу, ал
- бұрыштық үдеу, ал  деп белгіейік, сонда
деп белгіейік, сонда
 (8.22)
(8.22)
Алынған (8.22) өрнектің шешімі (8.16) өрнек шешіміне ұқсас болады:
 (8.23)
(8.23)
Сондықтан, аз тербелістер кезінде физикалық маятниктің ауытқуы уақыт бойынша гармониялық заң арқылы өзгереді. Олай болса, физикалық маятниктің аз тербелістер кезіндегі  периоды
периоды
 (8.24)
(8.24)
Бұл өрнекті техникада дененің инерция моментін олардың тербелістерінің периоды бойынша тәжірибелік анықтау кезінде жиі пайдаланады.
Математикалық маятник. Созылмайтын және салмақсыз жіпке ілінген, барлық массасы бір нүктеге жинақталған материалды нүктені математикалық маятник деп атайды. Тәжірибеде ұзындығы дененің сызықтық мөлшерінен көптеген есе үлкен болатын, жеңіл жіпке ілінген ауыр денені математикалық маятник деп есептеуге болады. Егер жіптің вертикалымен жасайтын аса үлкен емес 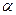 бұрышына маятникті тепе-теңдік қалпынан ауытқытып, содан оны еркін жіберсек, онда ол вертикал жазықтықта өзінің меншікті салмақ құрушысының әсерінен тербеле бастайды. Берілген жағдайда дененің инерция моменті
бұрышына маятникті тепе-теңдік қалпынан ауытқытып, содан оны еркін жіберсек, онда ол вертикал жазықтықта өзінің меншікті салмақ құрушысының әсерінен тербеле бастайды. Берілген жағдайда дененің инерция моменті  болады, мұндағы
болады, мұндағы  -математикалық маятник ұзындығы. Математикалық маятник физикалық маятниктің дербес түрі деп есептеп, (8.24) өрнегінен алатынымыз
-математикалық маятник ұзындығы. Математикалық маятник физикалық маятниктің дербес түрі деп есептеп, (8.24) өрнегінен алатынымыз
 (8.25)
(8.25)
(8.25)-тен: математикалық маятниктің тербеліс периоды тек маятник ұзындығына және ауырлық күші үдеуіне тәуелді, массасына тәуелсіз екені көрінеді. (8.24) және (8.25) өрнектерін салыстырсақ
 (8.26)
(8.26)
мұндағы  - физикалық маятниктің келтірілген ұзындығы.
- физикалық маятниктің келтірілген ұзындығы.
Келтірілген ұзындық деп тербеліс периоды физикалық маятниктің периодымен сәйкес келетін математикалық маятникті айтамыз.
Гюйгенс-Штейнер теоремасы бойынша
 (8.27)
(8.27)
мұндағы  - массалар центрі арқылы өтетін оське қатысты инерция моменті.
- массалар центрі арқылы өтетін оське қатысты инерция моменті.
Сондықтан, физикалық маятниктегі ОС түзу бойлап ұзындығы  түзу кесіндісін алайық.
түзу кесіндісін алайық. 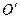 нүкте айналу центрі деп аталады. Бұл нүктені математикалық нүкте ретінде қабылдасақ, және осы нүктеге физикалық маятниктің барлық массасы жинақталған деп есепетесек, оның тербеліс периоды өзгермейді. Демек, маятниктің іліну нүктесі
нүкте айналу центрі деп аталады. Бұл нүктені математикалық нүкте ретінде қабылдасақ, және осы нүктеге физикалық маятниктің барлық массасы жинақталған деп есепетесек, оның тербеліс периоды өзгермейді. Демек, маятниктің іліну нүктесі  мен айналу центрі
мен айналу центрі 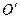 массалар центрі С нүктенің екі жағында жатады және массалар центрінен бірдей қашықтықта жатқан барлық іліну нүктелері үшін маятниктің келтірілген ұзындықтары
массалар центрі С нүктенің екі жағында жатады және массалар центрінен бірдей қашықтықта жатқан барлық іліну нүктелері үшін маятниктің келтірілген ұзындықтары  және тербеліс периодтары Т бірдей болады. Бұл жағдайда іліну нүктесі О мен айналу центрі
және тербеліс периодтары Т бірдей болады. Бұл жағдайда іліну нүктесі О мен айналу центрі 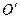 бір-бірімен орын алмасуы мүмкін.
бір-бірімен орын алмасуы мүмкін.
 (8.28)
(8.28)
Егер маятникті айналу центрі 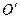 нүктесіне ілсек, оның тербеліс периоды өзгермейді, бұрынғы іліну нүктесі жаңа айналу центрі болады. Бұл тұжырым Гюйгенс теоремасы деп аталады.
нүктесіне ілсек, оның тербеліс периоды өзгермейді, бұрынғы іліну нүктесі жаңа айналу центрі болады. Бұл тұжырым Гюйгенс теоремасы деп аталады.
Гармониялық тербелістер жасайтын денелер кинетикалық және потенциалық энергияларға ие болады. Егер тербеліс  өрнекпен сипатталса, онда жүктің жылдамдығы
өрнекпен сипатталса, онда жүктің жылдамдығы  ға тең. Олай болса, дененің кинетикалық энергиясы
ға тең. Олай болса, дененің кинетикалық энергиясы
 (8.29)
(8.29)
 түріндегі күштің әсерінде тұрған жүйенің потенциалдық энергиясы
түріндегі күштің әсерінде тұрған жүйенің потенциалдық энергиясы  немесе
немесе  екендігін ескерсек, онда
екендігін ескерсек, онда
 (8.30)
(8.30)
Тербелістегі механикалық жүйенің толық энергиясы
 (8.31)
(8.31)
Кинетикалық және потенциалдық энергия уақыт бойынша өзгереді, жүйе тепе-теңдік күйден өткен кезде дененің жылдамдығы ең үлкен болады, сондықтан кинетикалық энергия максимал болады. Бұл мезетте квазисерпімді күш болмайды, сондықтан потенциалды энергия нольге тең. Тербелістегі әрі қарай қозғалу жағдайында квазисерпімді күштер теріс жұмыс жасайды, соның есебінен кинетикалық энергия кемиді, ал потенциалдық энергия артады. Тербеліс процесі кезінде кинетикалық энергия үздіксіз потенциалық энергияға ауысу және керісінше жағдайлар болып тұрады. Еркін тербеліс жасайтын тербелмелі жүйелердің ерекшелігі осында. (8.31) өрнек жүйенің толық энергиясы тұрақты болады.
Егер үйкеліс есепке алсақ, онда уақыттың өтуіне қарай жүйенің толық энергиясы кемиді. Меншікті тербеліс бұл жағдайда өшетін тербеліс болып табылады.
Өшетін тербелістер. Тұтқыр ортада тепе-теңдік нүктесі айналасында тербелген денеге, серпімді (немесе квазисерпімді) күшінен басқа қозғалыс жылдамдығына пропорционал  кедергі күші әсер етеді, мұндағы
кедергі күші әсер етеді, мұндағы 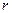 - кедергі коэффициенті, минус таңбасы
- кедергі коэффициенті, минус таңбасы  мен
мен  векторларының қарама-қарсы бағытта екенін көрсетеді. Бұл заңдылық қозғалыс жылдамдығы аз болған жағдайда орындалады.
векторларының қарама-қарсы бағытта екенін көрсетеді. Бұл заңдылық қозғалыс жылдамдығы аз болған жағдайда орындалады.
 күшін ескерсек, онда қозғалыс теңдеуі
күшін ескерсек, онда қозғалыс теңдеуі
 (8.32)
(8.32)
түріне келеді, мұндағы  дене массасы,
дене массасы, 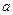 - оның үдеуі,
- оның үдеуі,  - қайтарушы күш. Үдеу
- қайтарушы күш. Үдеу  және жылдамдық
және жылдамдық  екенін ескерсек, өрнектерінің негізінде (8.32) теңдеуді мына түрде жазуға болады.
екенін ескерсек, өрнектерінің негізінде (8.32) теңдеуді мына түрде жазуға болады.
 (8.33)
(8.33)
(8.33) теңдеудің барлық мүшелерін 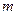 -ге бөліп және бұдан кейін
-ге бөліп және бұдан кейін
 (8.34)
(8.34)
белгілеулерін енгізсек, (8.33) теңдеу төмендегі көріністе болады
 (8.35)
(8.35)
1Сонымен, тұтқыр ортадағы дененің тербелісін біртекті екінші дифференциалдық теңдеумен сипаттауға болады, оның тұрақты шамалары 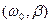 жүйе параметрлерін
жүйе параметрлерін  тәуелді болады.
тәуелді болады.
Диференциалды теңдеу теорияларында  , шарты кезінде (8.35) теңдеуінің шешуі мынадай түрде болады:
, шарты кезінде (8.35) теңдеуінің шешуі мынадай түрде болады:
 (8.36)
(8.36)
мұндағы 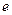 - натурал логарифмнің негізі. (8.36) өрнегінен тербеліс амплитудасы
- натурал логарифмнің негізі. (8.36) өрнегінен тербеліс амплитудасы
 (8.37)
(8.37)
екені шығады, яғни тербеліс амплитудасы уақыт бойынша экспонент бойынша азаяды, сондықтан бұл тербеліс өшетін тербеліс деп аталады (8.6-сурет)


Өшетін тербелістер жиілігі 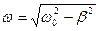 , ал оның периоды
, ал оның периоды
 (8.38)
(8.38)
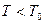 екеніне көз жеткізу қиын емес, мұндағы
екеніне көз жеткізу қиын емес, мұндағы  -еркін тербелістер периоды, яғни
-еркін тербелістер периоды, яғни  кезіндегі болатын тербеліс.
кезіндегі болатын тербеліс.
Тербелістердің өту дәрежесінің көрсеткіші ретінде өшу декременті деп аталатын шама енгізілген. Ол  және
және  уақыт мезеттеріне сәйкес келетін амплитудалар қатынасына тең, яғни
уақыт мезеттеріне сәйкес келетін амплитудалар қатынасына тең, яғни
 (8.39)
(8.39)
Берілген өрнектің натурал логарифмі өшудің логарифмді декременті  деп аталады:
деп аталады:
 (8.40)
(8.40)
 физикалық мәні келесі жағдайда ашылуы мүмкін. Айталық
физикалық мәні келесі жағдайда ашылуы мүмкін. Айталық  уақыт аралығы өткен кезде амплитуда
уақыт аралығы өткен кезде амплитуда  рет кемиді делік. Бұл деген сөз
рет кемиді делік. Бұл деген сөз  , сондықтан
, сондықтан  .
.
Сонда логарифмдік декремент мына түрде көрсетуге болады  .
.
Егер реалаксация уақыты деп аталатын  уақыт кезінде
уақыт кезінде 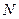 тербеліс жасалса, яғни
тербеліс жасалса, яғни  болса, онда
болса, онда  .
.
Сонымен, логарифмдік декремент  - тербеліс санына кері шама, амплитудасы
- тербеліс санына кері шама, амплитудасы 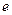 рет кемиді (шамамен 3 рет кемиді, өйткені
рет кемиді (шамамен 3 рет кемиді, өйткені  ). Егер
). Егер  болса, онда
болса, онда  болады.
болады.  шамасы арқылы тербелмелі жүйенің сапалылық деп аталатын тағы да бір сипаттамасы анықталады:
шамасы арқылы тербелмелі жүйенің сапалылық деп аталатын тағы да бір сипаттамасы анықталады:  теңдеуінен, амплитудасы
теңдеуінен, амплитудасы 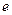 есе азайтқанға дейін неғұрлым көп тербеліс жасалса, тербелмелі жүйе соғұрлым сапалы болып табылады.
есе азайтқанға дейін неғұрлым көп тербеліс жасалса, тербелмелі жүйе соғұрлым сапалы болып табылады.
Еріксіз тербелістер. Жалпы алғанда сыртқы күштердің әсерінен қозатын тербелістерді еріксіз тербелістер деп атайды. Сыртқы күштер әсер еткен жағдайда жүйе сол күштің жиілігімен тербеледі. Денеге  серпімді күш және
серпімді күш және  кедергі күшінен басқа
кедергі күшінен басқа  гармониялық заңмен өзгеретін
гармониялық заңмен өзгеретін  айнымалы күші әсер еткен жағдайды қарастырайық мұндағы
айнымалы күші әсер еткен жағдайды қарастырайық мұндағы  -оның амплитудалық мәні,
-оның амплитудалық мәні,  -жиілігі. Бұл кезде Ньютонның екінші заңы мына түрге келеді:
-жиілігі. Бұл кезде Ньютонның екінші заңы мына түрге келеді:
 (8.41)
(8.41)
Теңдік мүшелерін 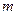 -ге бөліп және қосымша
-ге бөліп және қосымша  белгілеуін енгізсек, теңдеу мына түрге келеді
белгілеуін енгізсек, теңдеу мына түрге келеді
 (8.42)
(8.42)
Бұл еріксіз тербелістердің теңдеуі деп аталады. Жүйенің тербелісі гармониялық болып тұрақты коэффициенттері бір және екінші ретті біртекті емес дифференциалды теңдеу арқылы өрнектеледі. Бұл теңдеудің жалпы шешімі:
 (8.43)
(8.43)
(8.43) теңдеуінен 

Енді  мәндерін (8.42)-ке қойсақ, онда
мәндерін (8.42)-ке қойсақ, онда
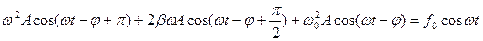 (8.44)
(8.44)
(8.44) өрнегі, үш гармониялық тербелістерді қосудың нәтижесі теңдіктің оң жағымен сипатталтын төртінші өрнек болатындығын дәлелдейді. Тербелісі қосу суреті көрнекті болар еді, егер диаграмма әдісін пайдалансақ.
Ол үшін тіреу осі ОХ-ті (8.7-сурет) қосылатын тербелістерді амплитудалық векорлары  уақыты мезетінде тіреу сызықтарымен:
уақыты мезетінде тіреу сызықтарымен:
 ,
,  және
және  бұрыштарын жасайтындай етіп таңдап аламыз:
бұрыштарын жасайтындай етіп таңдап аламыз:


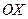 осіне сондай бұрыштармен
осіне сондай бұрыштармен  және
және  саламыз. Олардың қосындысы
саламыз. Олардың қосындысы 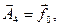 -ге тең, яғни
-ге тең, яғни
 (8.45)
(8.45)
8.7-сурет бойынша еріксіз тербелістердің амплитудасы
 (8.46)
(8.46)
ал жүйенің еріксіз күші мен ығысуының арасындағы фаза айырымы
 (8.47)
(8.47)
(8.46) теңдеуінен, еріксіз тербелістердің амплитудасы еріксіз күштің  жиілігінен тәуелді болатынын көрсетеді. Ол максимум мәніне шарты кезінде жетеді
жиілігінен тәуелді болатынын көрсетеді. Ол максимум мәніне шарты кезінде жетеді
 (8.48)
(8.48)
Бұл кездегі  жиілікті резонанстық жиілік деп атайды, ал құбылыстың өзін резонанс деп атайды. Егер
жиілікті резонанстық жиілік деп атайды, ал құбылыстың өзін резонанс деп атайды. Егер  болса, яғни тербелістің өшуі жоқ, онда
болса, яғни тербелістің өшуі жоқ, онда  , ал амплитуда бұл кезде шексіз үлкен болады. Реалды (нақты) жүйелерде
, ал амплитуда бұл кезде шексіз үлкен болады. Реалды (нақты) жүйелерде 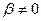 болғандықтан, амплитуда өзінің максимал мәндеріне жетеді және шекті болып қалады.
болғандықтан, амплитуда өзінің максимал мәндеріне жетеді және шекті болып қалады.
Толқындар. Толқынның серпімді ортада таралуы. Егер өзара байланысқан бөлшектерден тұратын орта берілсе, онда оның бір бөлшегі қозғалса, соның нәтижесінде басқа болшектерде қозғала бастайды. Осындай ортаның бір бөлшегінің тербелісінің нәтижесінде сол арада толқын тарайды. Мысалы, су бетінің тас түскен жерінің аймағы тербеледі. Бұл тербеліс осы аймақтан жан-жаққа тарала бастайды да, судың бетіне толқын пайда болады. Тербеліс тараған кезде тербелуші бөлшектер тербеліс процесімен бірге орын ауыстырмай, өзінің тепе-теңдік маңында тербеледі. Егер бөлшектер тербеліс таралатын түзудің бойымен тербелетін болса онда мұндай толқынды қума толқын дейміз. Ал бөлшектердің тербелісі тербелістердің тарау бағытына перпендикуляр болса, онда мұндай толқын көлденең толқын деп аталады.
Мысалы сұйықтар мен газдарда тек қума толқындар тарайды. Қатты денелерде көлденең толқындармен қатар қума толқындар да тарай алады. Белгілі бір уақыт кезеңінде тербеліс жеткен нүктелерінің геометриялық орнын толқын фронты деп атайды. Толқын фронтының барлық нүктелері бірдей фазада тербеледі. Толқын фронтының әрбір нүктесі жаңа толқын көзі бола алады. Бұны Гюйгенс принципі деп атайды.


8.8-сурет
Толқын теңдеуі. Бір ұшы байлаулы тұрған жіптің бойымен тараған толқынды қарастырайық. А – тербеліс көзі. Тербеліс көзінің теңдеуін былай жазуға болады:
 (8.49)
(8.49)
Енді А нүктесінен  ара қашықтықта тұрған В нүктесінен алайық. Тербелістер В нүктесіне бір
ара қашықтықта тұрған В нүктесінен алайық. Тербелістер В нүктесіне бір  уақытта жетіп, В нүтесінде тербеліске келеді. В нүктесінің тербеліс теңдеуі мынадай болады:
уақытта жетіп, В нүтесінде тербеліске келеді. В нүктесінің тербеліс теңдеуі мынадай болады:
 (8.50)
(8.50)
В нүктесі тербеле бастаған кезден бастап есептелетін уақыт, яғни  , осындағы
, осындағы  - тың мәнін (8.49) теңдікке қойсақ:
- тың мәнін (8.49) теңдікке қойсақ:
 (8.51)
(8.51)
Жалпы түрде толқынның теңдеуі былай жазылады:

Мұнда: А – тербелістің амплитудасы,  - дөңгелектік жылдамдық,
- дөңгелектік жылдамдық,  - толқынның фазасы,
- толқынның фазасы,  - толқынның бастапқы фазасы.
- толқынның бастапқы фазасы.
Толқындардың суперпозициясы. Толқынның топтық жылдамдығы. Бір ортада бірнеше толқын кездессе, олар өзара қабаттасады. Осындай екі, немесе бірнеше толқындардың қабаттасуын толқынның суперпозиция принципі дейді. Жиіліктерінде азғантай айырмашылықтары бар толқындар суперпозициясы толқындық пакет дейді. Мысалы, бір бағытта тараған, жиіліктерінің айырымы өте аз ( және
және  ) екі гармониялық тербелістің қосындысын қарастырайық:
) екі гармониялық тербелістің қосындысын қарастырайық:

Гармониялық емес толқынның тарау жылдамдығы үшін оның максимум амплитудасының ығысу жылдамдығын алады. Максимум амплитудасы болу шарты  ;
;  , мұндағы
, мұндағы  - топтық жылдамдық.
- топтық жылдамдық.
Топтық жылдамдық пен фазалық жылдамдықтың арасында мынадай байланыс бар:
 (8.52)
(8.52)
Толқынды сипаттау үшін толқындық сан деген ұғым пайдалынады.
 (8.53)
(8.53)
Осыны ескеріп толқынның теңдеуін былай жазуға болады:
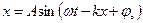 (8.54)
(8.54)
Толқынның фазасын тұрақты деп алсақ, 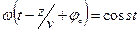
 ;
;  ;
;  -фазалық жылдамдық. (8.53) формуланы пайдаланып фазалық жылдамдықты былай жазуға болады:
-фазалық жылдамдық. (8.53) формуланы пайдаланып фазалық жылдамдықты былай жазуға болады:  .
.
Жалпы біртекті изотопты ортада тараған толқынның теңдеуі былай жазылады
 немесе
немесе 
мұндағы  - Лаплас операторы.
- Лаплас операторы.
Акустикадағы Доплер эффектісі. Дыбыс көзі мен дыбыс қабылдаушының ара қашықтықтары өзгергенде, дыбыс қабылдаушыға келетін дыбыс толқынының жиілігінің өзгеруін Доплер құбылысы дейді.
1.Дыбыс көзі мен дыбыс қабылдаушының аралары өзгермей тұрақты болса,  ; (
; ( - дыбыс көзінің,
- дыбыс көзінің,  - дыбыс қабылдаушының жылдамдықтары) ортада дыбыстың таралу жылдамдығы
- дыбыс қабылдаушының жылдамдықтары) ортада дыбыстың таралу жылдамдығы  болса, онда дыбыс толқының ұзындығы
болса, онда дыбыс толқының ұзындығы  болады. Сонда қабылдаушыға жеткен дыбыс толқынының жиілігі
болады. Сонда қабылдаушыға жеткен дыбыс толқынының жиілігі 
 ; Осыдан, қарастырылып отырған жағдайда қабылдаушыға жеткен дыбыс толқынның жиілігі (
; Осыдан, қарастырылып отырған жағдайда қабылдаушыға жеткен дыбыс толқынның жиілігі ( ) дыбыс көзінің шығарған толқынның жиілігіне тең болатынын көреміз. (
) дыбыс көзінің шығарған толқынның жиілігіне тең болатынын көреміз. ( )
)
2.Дыбыс көзі тұрақты, қабылдаушы дыбыс көзіне қарай қозғалады.  ,
,  . Бұл жағдайда қабылдаушымен салыстырғанда дыбыс толқынның жылдамдығы (
. Бұл жағдайда қабылдаушымен салыстырғанда дыбыс толқынның жылдамдығы ( ) болады. Сонда
) болады. Сонда  ; Осыдан қабылдаушыға жеткен дыбыс толқынның жиілігі, дыбыс көзінің шығарған толқынның жиілігінен
; Осыдан қабылдаушыға жеткен дыбыс толқынның жиілігі, дыбыс көзінің шығарған толқынның жиілігінен  есе көп болатынын көреміз.
есе көп болатынын көреміз.
3.Қабылдаушы тыныштыққа, ал дыбыс көзі қабылдаушыға қарай қозғалады.  ,
,  . Бұл жағдайда бір период кезінде дыбыс көзінен шыққан толқын
. Бұл жағдайда бір период кезінде дыбыс көзінен шыққан толқын 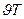 жол жүреді, ал
жол жүреді, ал  толқын ұзындығынан тең болады. Осы уақыт ішінде дыбыс көзі дыбыс толқынның тарау бағытымен жол жүреді. Сондықтан, дыбыс толқынын қысқартып
толқын ұзындығынан тең болады. Осы уақыт ішінде дыбыс көзі дыбыс толқынның тарау бағытымен жол жүреді. Сондықтан, дыбыс толқынын қысқартып  болады.
болады.  осыдан қабылдаушыға жеткен дыбыс толқынның жиілігі
осыдан қабылдаушыға жеткен дыбыс толқынның жиілігі  есе артады.
есе артады.
4. Қабылдаушы мен дыбыс көзі бір-бірімен салыстырғанда қозғалыста болса, 2 және 3 жағдайлардың қорытындысын пайдаланып, қабылдаушының қабылдайтын толқынының жиілігін былай жазамыз:  ; Мұндағы (+) таңбасы қабылдаушы мен дыбыс көз бір-біріне жақын да, ал (-) таңбасы олар бір-бірінен алыстағандағы жағдайларға сәйкес келеді.
; Мұндағы (+) таңбасы қабылдаушы мен дыбыс көз бір-біріне жақын да, ал (-) таңбасы олар бір-бірінен алыстағандағы жағдайларға сәйкес келеді.
МОДУЛЬ






