1. По заданным параметрам выстраиваем проекции конуса и цилиндра, при этом на горизонтальной проекции ось цилиндра проходит параллельно оси ОХ и совпадает с горизонтальной осью основания цилиндра. Так как цилиндр расположен под углом, то правое основание будет видимым в виде эллипса. Для построения эллипса находим характерные точки большой и малой осей эллипса. Отмечаем точки a', b', c', d'; так как точки a' и c' лежат на очерковых образующих цилиндра, то они будут лежать на оси цилиндра на горизонтальной плоскости проекций. И наоборот, точки b' и d' лежат на оси цилиндра на фронтальной плоскости проекций, тогда на горизонтальной плоскости проекций они будут лежать на очерковых образующих цилиндра. Полученные точки a, b, c, d соединяем плавной линией. С левой стороны достраиваем аналогично.
2. Отмечаем характерные точки пересечения очерковых образующих конуса и цилиндра: 1', 2', 3', 4'.
3. Остальные точки на фронтальной плоскости проекций находим с помощью проекций вспомогательных сфер, строим окружности из центра пересечения осей конуса и цилиндра е’. Например: берем радиус r1 произвольно и строим окружность. Отмечаем точки пересечения данной окружности с образующими конуса (точки хх) и пересечение с образующими цилиндра (точки уу). Полученные точки соединяем прямыми линиями и отмечаем точки пересечения этих прямых между собой (т. е. при пересечении хх и уу отмечаем точки 5', 12' и 10'). Остальные вспомогательные сферы (окружности) выбираем произвольно, главное чтобы они не выходили за самую крайнюю характерную точку (в данном случае это точка 1 ').
4. Самая минимальная окружность должна быть вписана либо в цилиндр либо в конус так, чтобы она касалась одну фигуру и пересекала другую. В данном примере эта окружность вписана в цилиндр, следовательно, в цилиндре будет выстроена только одна вспомогательная линия уу, а общих точек пересечения только две (6' и 11').
5. Ближние точки соединяем между собой, получаем две кривые 2'6'5'3' и 1 ' 7 ' 8 ' 9 ' 10 ' 11 ' 12 ' 13 ' 4 '. В данном примере линии идут близко к образующим цилиндра, в других вариантах они могут идти близко к образующим конуса.
6. Находим точки на горизонтальной плоскости проекций. Сначала можем найти характерные точки 1, 2, 3, 4. Эти точки будут лежать на горизонтальной оси основания конуса, т. к. на фронтальной плоскости проекций они лежат на очерковых образующих конуса.
7. Все остальные точки находим с помощью вспомогательных окружностей. Каждая точка находится на вспомогательной линии хх, принадлежащей конусу (эти линии получены при построении проекций сфер). Так как линии проходят параллельно основанию конуса, то в сечениях получаются окружности, радиусы которых измеряются от оси конуса до очерковой образующей (см. радиус r1 для точки 5'). Вспомогательные окружности строим на горизонтальной плоскости проекций из точки О. Затем на данную окружность сбрасываем точки.
8. Дальше определяем видимость кривой пересечения. Смотрим сверху: боковая поверхность конуса будет видна полностью, а боковая поверхность цилиндра будет видимой до оси цилиндра и невидимой под осью цилиндра. Так как кривая 1'7'8'9'10'11'12'13'4' на фронтальной плоскости проекций пересекает ось цилиндра в точках t1’ и t2’, то на горизонтальной плоскости проекций часть кривой t1 11 t2 будет видимой (она проходит над осью цилиндра). Остальная часть кривой будет невидимой, так как на фронтальной плоскости остальные точки расположены под осью цилиндра. Линия 2 – 6 – 5 – 3 – 5 – 6 – 2 будет видимой, так как на фронтальной плоскости проекций эти точки расположены над осью цилиндра. Остается показать невидимой линией часть основания конуса, расположенного под проекцией цилиндра.
Вопросы к экзамену
1. Сущность метода проекций и его отличие от других методов отображения предметов. Что называется проекцией объекта?
2. Какие проекции называют центральными и каковы их свойства? Какие проекции называют параллельными, их варианты и свойства?
3. Сущность метода ортогонального проецирования. Его преимущества. Определение основных элементов в методе ортогонального проецирования.
4. Что называется ортогональной проекцией точки на плоскости проекций? Как определяют положение точки в трехмерном пространстве?
5. Какие проекции называют аксонометрическими? Недостатки аксонометрических изображений и способы их устранения.
6. Задание и изображение прямой на чертеже. Прямая общего положения.
Прямая частного положения.
7. Какие прямые называют линиями уровня? Их изображения, особенности, названия. Какие прямые называют проецирующими? Их изображения, названия.
8. Как определяется натуральная величина отрезка прямой?
9. Как определяют угол наклона прямой к плоскости проекций?
10. Следы прямой, их определение. Изображение параллельных прямых на эпюре. Особенности доказательства параллельности профильных прямых.
11. Чем доказывается пересечение двух прямых, заданных проекциями?
12. В каких случаях прямой угол проецируется в истинную величину?
13. Какие линии называют скрещивающимися? Их изображение на эпюре.
14. Какие точки называют конкурирующими?
15. Как определяется видимость элементов предметов на проекциях?
16. Способы задания плоскости в пространстве. Что называют следами плоскости?
17. Какие плоскости называют плоскостями общего положения?
18. Какие плоскости являются плоскостями частного положения? Их изображение, название, характеристика.
19. Принадлежность точки и прямой данной плоскости.
20. Главные линии плоскости. Их изображение, название, характеристика.
21. Какие плоскости являются параллельными? Способы их задания на эпюре.
22. Какие задачи называют позиционными, а какие - метрическими?
23. Как определяются линии пересечения двух плоскостей?
24. Как определяется параллельность линии заданной плоскости?
25. Алгоритм построения точки пересечения прямой с плоскостью.
26. Условия перпендикулярности прямой к плоскости.
27. Алгоритм решения задачи по определению расстояния от точки до плоскости.
28. Условия взаимной перпендикулярности плоскостей.
29. Назначения способов преобразования проекций. Задачи, решаемые с помощью этих способов.
30. Способ замены плоскостей проекций. Сущность способа. Методика
выполнения преобразований.
31. Способ вращения вокруг проецирующих осей. Сущность способа. Методика выполнения преобразований.
32. Способ плоскопараллельного перемещения. Сущность способа. Методика выполнения преобразований.
33. Сущность способа вращения вокруг линии уровня и способа совмещения. Последовательность решения задач.
34. Кривые линии. Свойства проекций кривой линии. Свойства точек кривой линии.
35. Касательная и нормаль к кривой линии.
36. Кривизна плоской кривой.
37. Проецирование кривых линий.
38. Задание пространственной кривой на чертеже.
39. Классификация поверхностей.
40. Что называют каркасом некинематической поверхности? Примеры каркасов поверхностей.
41. Контур поверхности, очерк поверхности.
42. Поверхности вращения. Основные линии на поверхности вращения.
43. Наиболее распространенные многогранники и их основные элементы.
44. Сущность построения сечения многогранника плоскостью.
45. Как строятся проекции сечения гранного тела плоскостью? Алгоритм определения точек пересечения многогранника прямой линией.
46. Способы построения линии взаимного пересечения многогранных поверхностей.
47. Алгоритм построения точек пересечения прямой линии поверхностью.
48. Алгоритм построения линии пересечения кривой поверхности плоскостью.
49. Посредники. Их виды, назначение и способы применения для решения задач на пересечение тел. Алгоритм построения линии пересечения поверхностей.
50. Сущность развертывания поверхности. Что называется разверткой поверхности?
51. Приемы развертывания гранных поверхностей.
52. Системы координат, используемые при изображении предметов на чертеже. Изображения на технических чертежах. Расположение основных видов. Различия между проекцией и видом.
Задача к билетам №1, 17

 Задача к билетам №2, 18
Задача к билетам №2, 18
Задача к билетам №3, 19
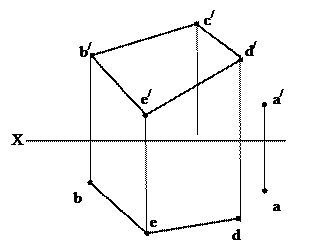 |
 Задача к билетам №4, 20
Задача к билетам №4, 20
Задача к билетам №5, 21

Задача к билетам №6, 22

Задача к билетам №7, 23

Задача к билетам №8, 24

Задача к билетам №9, 25

Задача к билетам №10
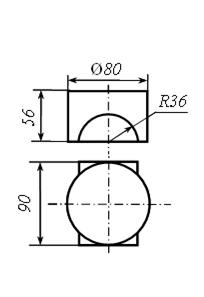
Задача к билетам №11

Задача к билетам № 12

Задача к билетам №13

Задачи к билетам №14

Задача к билетам № 15

Задача к билетам № 16

Список литературы
Основная
1. Короев Ю.И. Начертательная геометрия: Учебник для вузов. М.: Архитектура, 2004, 422 с.
2. Боголюбов С.К., Воинов А.В. Черчение. М.: Машиностроение, 1984, 303 с.
Дополнительная
3. Грачев Е.В. Методические указания по изучению дисциплины «Начертательная геометрия. Инженерная графика» для курсантов и слушателей по специальности 280104.65., СПб УГПС, 2007.
4. Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии: Учебник для вузов. М.: Наука, 1973.






