1. По координатам строим проекции точек О, О' и S, S'. От точки О' откладываем радиус R основания конуса на фронтальной плоскости проекций и соединяем полученные точки с вершиной конуса S', получим проекцию конуса. На горизонтальной плоскости проекций чертим окружность с центром в точке О и радиусом R. Из точки S проводим касательные к окружности (основание конуса), получим вторую проекцию конуса.
2. Строим по координатам точку е' (центр основания цилиндра) на фронтальной плоскости проекций и из полученной точки чертим окружность радиусом r ц, получим проекцию фронтально-проецирующего цилиндра. На горизонтальной плоскости проекций строим ось цилиндра параллельно оси ОY. Основания цилиндра вычерчиваем перпендикулярно к оси цилиндра и располагаем их за проекцией конуса, при этом длина цилиндра будет приблизительно равна 4 r ц.
3. Отмечаем характерные точки пересечения очерковых образующих конуса и цилиндра на фронтальной плоскости проекций. Это точки 1', 2' и 10'. Далее проводим касательную к окружности цилиндра, исходящую из вершины конуса S', и восставляем к касательной перпендикуляр, проходящий через центр окружности основания цилиндра, полученную точку отмечаем 3'.
4. Так как на горизонтальной плоскости проекций необходимо будет показать видимость линии пересечения, то определяем границы видимости для конуса. Границами видимости будут крайние очерковые образующие конуса на горизонтальной плоскости проекций; отмечаем точки касания образующих с основанием конуса, при этом помним, что точка касания лежит на перпендикуляре, восставленном из центра окружности к образующей, отмечаем точки b и c1. Дальше находим проекции этих точек на фронтальной плоскости проекций; основание конуса лежит на оси ОХ, следовательно, поднимаем проекции точек на ось ОХ (b' и c1') и соединяем их с вершиной конуса S', получим образующие b'S' и c1'S'. Построенные образующие пересекают очерк цилиндра в точках: 4', 5', 6 и 7'.
5. На горизонтальной плоскости проекций необходимо учесть видимость цилиндра: это левая образующая цилиндра. На фронтальной плоскости проекций проводим вспомогательную образующую конуса через точку пересечения окружности основания цилиндра с горизонтальной осью, отмечаем точки 8' и 9'.
6. Остается большой промежуток между точками 4' и 10', необходимы дополнительные точки. Строим промежуточную образующую s'к' произвольно и отмечаем точки 11' и 12'.
7. Строим все образующие на горизонтальной плоскости проекций и сбрасываем на них соответствующие точки. Например, строим образующую аs (их будет две) и проецируем на них точки 3. Аналогично достраиваем все точки.
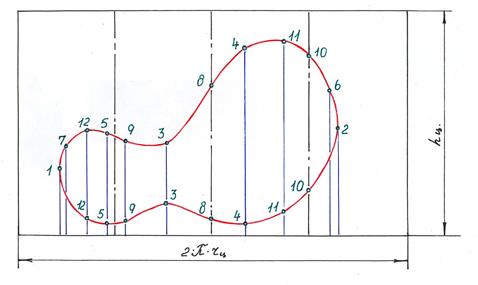
8. Точки на горизонтальной плоскости проекций соединяем в том порядке, в каком они обозначены на фронтальной проекции цилиндра, т. е. 1-7-12-5-9-3-8-4-11-10-6-2-6-10-11-4-8-3-9-5-12-7-1.
9. Определяем видимость кривой: смотрим на фронтальной плоскости проекций (по направлению взгляда, обозначенного стрелкой). Все точки, лежащие над горизонтальной осью цилиндра, будут видимыми (1', 7', 12', 5', 9', 3', 8'), под ней – невидимыми. Но на горизонтальной плоскости проекций необходимо учитывать границы видимости конуса – точки 7 и 5. Тогда видимыми будут следующие части кривой: 8 – 3 – 9 – 5 – 12 – 7 и 8 – 3 – 9 – 5.
Задача № 9
Построить развертку наклонного конуса и развертку цилиндрической поверхности с нанесением на развертках линии их пересечения.
Указания к решению задачи № 9
Исходные данные для решения берутся из задачи № 8. Для построения развертки наклонного конуса на поверхности конуса проводят ряд образующих и находят их истинные длины. Эти построения следует выполнить тонкими линиями на чертеже при решении задачи № 8. Затем методом раскатки, используя истинные длины образующих и хорды на основании конуса, строят развертку конической поверхности. Далее наносят линию пересечения конуса с цилиндром. Развертка цилиндра представляет собой прямоугольник с размерами, равными длине цилиндра и длине основания окружности цилиндра. На развертке цилиндра также показывают линию пересечения конуса с цилиндром. Все построения показать тонкими линиями. Точки на линии пересечения должны иметь те же обозначения, что и на проекционном чертеже.
Пример решения задачи №9