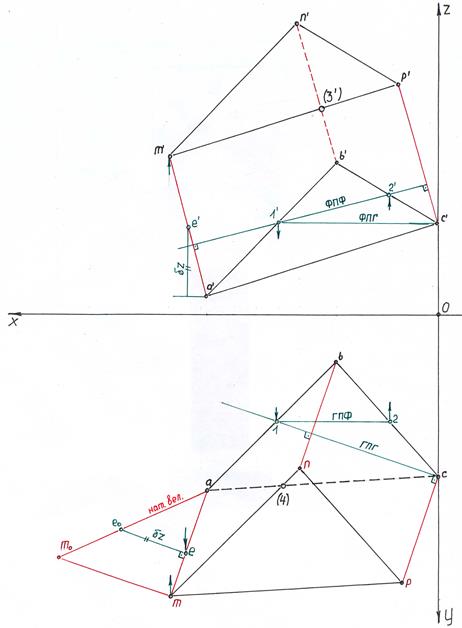
1. Строим проекции треугольников по заданным координатам точек.
2. Берем проецирующую плоскость Q н по стороне треугольника kde и отмечаем точки 1 и 2 в треугольнике аbс. Находим вторые проекции данных точек на фронтальной плоскости проекций: 1¢ – на стороне a ¢ – b ¢, 2 ¢ – на стороне a ¢ c ¢ (не забывая о том, что проекции точек находятся на одной линии связи, перпендикулярной к оси ОХ).
3. Соединяем между собой построенные точки 1 ¢ – 2 ¢ и продолжаем линию до пересечения со стороной e ¢ – d ¢ (так как по данной стороне брали проецирующую плоскость). Получим первую точку будущей линии пересечения треугольников f ¢, находим ее вторую проекцию на горизонтальной плоскости H – точку f на ed.
4. Вторую проецирующую плоскость Py берем по стороне d ¢ k ¢, отмечаем точки пересечения со сторонами треугольника a' b ¢ c’: точку 3’ на стороне a'b' и точку 4' на стороне a'b'. Находим вторые проекции данных точек на горизонтальной плоскости проекций (точку 3 на стороне a b и точку 4 на a c).
5. Соединяем полученные точки 3–4 прямой линией и отмечаем точку пересечения полученной прямой со стороной d k (так как по данной стороне брали проецирующую плоскость). Получим точку n – вторую точка линии пересечения треугольников. Находим вторую проекцию n' точки n на стороне d' k'.
6. На фронтальной плоскости проекций соединяем точки f' и n', на горизонтальной плоскости проекций соединяем точки f и n, т. е. строим проекции линии пересечения треугольников ABC и KDE. Отмечаем точки m и m' при пересечении стороны a b и a' b', соответственно линии m' n' и m n и есть линии пересечения треугольников, т. к. линия должна находиться внутри наложения треугольников.
7. Определяем видимость треугольников относительно друг друга методом конкурирующих точек. Для этого на фронтальной плоскости проекций берем любую общую точку, принадлежащую обоим треугольникам, например точку 3', она принадлежит стороне a' b' и стороне d' k'. Мысленно находим проекции этой точки на горизонтальной плоскости проекций: прямая с точкой 3, которая встретится первой, т. е. будет ближе к оси OX, на фронтальной плоскости проекций будет невидимой. В данном примере это точка 3 на стороне а b, следовательно, сторона a' b' от точки 3' до точки m' будет невидимой, после точки m' сторона a' b' будет видимой. Сторона d' k' от точки 3' до точки n' будет видимой, после точки n' станет невидимой до точки 4'. Дальше отрезок 4' 2' будет видимым, а сторона e' k' под вершиной m' a' 4' будет невидимой.
8. Аналогично определяется видимость на горизонтальной плоскости проекций. Например, возьмем общую точку 1 для сторон ab и ed, мысленно находим их на фронтальных проекциях данных сторон; та из них которая будет ближе к оси OX, и будет невидимой на горизонтальной плоскости проекций. Первой встречается ab, следовательно, отрезок 1m будет невидимым. Затем пойдет чередование видимых и невидимых частей (см. чертеж).
9. Строим натуральную величину треугольника ABC. Для этого необходимо расположить треугольник таким образом, чтобы его спроецировать в прямую линию, тогда его можно будет развернуть до положения, параллельного одной из плоскостей проекций, и спроецировать на нее в натуральную величину. Строим на фронтальной плоскости проекций линию с' 5' (ФПГ), находим вторую проекцию (точку 5) и строим линию c 5 (ГПГ).
10. Методом плоскопараллельного переноса разворачиваем треугольник на горизонтальной плоскости проекций так, чтобы линия c 5 была перпендикулярна к оси OX. На свободном месте поля чертежа справа от вычерченных треугольников проводим линию перпендикулярно к оси OX. На ней произвольно откладываем точку c1. Замеряем отрезок c 5 и откладываем его от точки c1 на выстроенном перпендикуляре, отмечаем точку 51. Чтобы выстроить треугольник a1 b1 c1, используем метод триангуляции (построение третьей точки по двум заданным имеющимися отрезками). Из точки с1 проводим дугу c1 b1 (отрезок с1 b1 равен отрезку cb), из точки 51 проводим дугу 51b1 (отрезок 51b1 равен отрезку 5b). Точку a1 находим аналогично.
11. Строим фронтальную проекцию треугольника, вычерчивая проецирующие линии связи перпендикулярно к осям из точек a', b', c' и a1, b1, c1. Проекция треугольника преобразуется в прямую b1' c1' a1' (так как он занимает частное положение), с помощью метода вращения разворачиваем ее до положения, параллельного оси OX, получим новую проекцию b2'c2'a2' и достраиваем натуральную величину треугольника b2 c2 a2.
12. Показываем на чертеже истинное положение линии пересечения треугольников. Точка m лежит на стороне ab, а точка n расположена внутри треугольника abс, следовательно, её необходимо зафиксировать. Продолжим отрезок mn до пересечения со стороной ac и отметим точку x. Переносим циркулем отрезки am на сторону a1b1 и ax на сторону a1c1, отмечаем точки m1 и x1, соединяем их и откладываем от точки m1 отрезок m1n1, равный отрезку mn. Переносим выстроенные точки на натуральную величину треугольника, как показано на чертеже.
Задача № 4
Построить проекции прямой призмы, основанием которой является треугольник ABC. Боковые ребра призмы строят длиной H = 55 мм. Данные берут из таблицы 2.
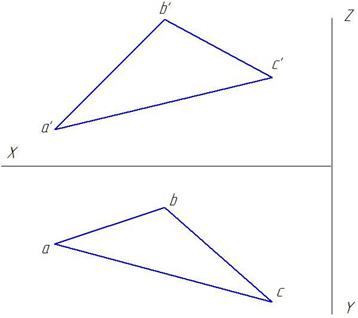
Указания к решению задачи № 4
Согласно варианту, по координатам точек A, B и C строят их проекции, которые определяют треугольник ABC. В одной из точек к плоскости треугольника ABC восставляют перпендикуляр произвольной длины. Далее на построенном перпендикуляре от вершины треугольника откладывается длина H, равная, по условию, высоте призмы. После этого строят верхнее основание призмы и определяют видимость чертежа. Видимые ребра показывают сплошными толстыми линиями, невидимые – штриховыми линиями. Все необходимые построения выполняются четкими линиями толщиной, равной ¼ толщины контурных линий.
Пример 1 для задачи 3