Методические рекомендации по выполнению
контрольных работ для обучающихся по дисциплине «Начертательная геометрия. Инженерная графика»
СМК-УМК 4.4.2-30-12
Введение
Самоконтроль усвоения учебного материала осуществляется при решении рекомендованных программой и методическими указаниями задач и ответов на задачи ивопросы. Текущий контроль преподавателя за работой слушателя-заочника производится по контрольным работам, выполняемым слушателем после изучения соответствующие разделов и тем.
Контрольная работа включает задания на выполнение заданий по начертательной геометрии и машиностроительному черчению. Нумерация заданий соответствует последовательности изучения материала.
Задания на контрольные работы индивидуальные. Слушатель должен выполнить тот вариант задачи, номер которого соответствует последней или предпоследней цифре его зачетной книжки.
Выполняемые чертежи должны размещаться так, чтобы равномерно заполнять все свободное поле листа выбранного формата. Чертежи должны выполняться карандашом твердостью 2Т или 2Н. Толщина линий чертежа должна соответствовать требованиям ГОСТ 2.303-68, а надписи, цифры и буквы - ГОСТ 2.304-68.
На рецензию контрольная работа представляется в полном объеме, Проверенную контрольную работу возвращают слушателю, и она хранится до зачета. Замечания преподавателя должны быть приняты к исполнению. Если контрольная работа не зачтена или зачтена не полностью то на повторную рецензию следует представлять всю контрольную работу. Слушатель допускается к сдаче зачета только после того, как представит все контрольные работы и рецензии к ним.
Задания к разделу 1 «Начертательная геометрия».
Общие рекомендации по разделу 1.
Выполнению графических работ должно предшествовать глубокое изучение соответствующих разделов учебно-справочной литературы.
Номер варианта задания должен выбираться по номеру зачетной книжки.
Все задания необходимо выполнять на стандартных листах ватмана формата А4 или А3. Основную надпись следует выполнять по ГОСТ 2.104-68 (рис. 1). Основная надпись чертежа располагается в правом нижнем углу формата (над нижней линией рамки). На листах формата А4 основная надпись всегда располагается вдоль короткой его стороны, т.е. формат А 4 располагается таким образом, чтобы его длинные стороны были бы вертикальны.
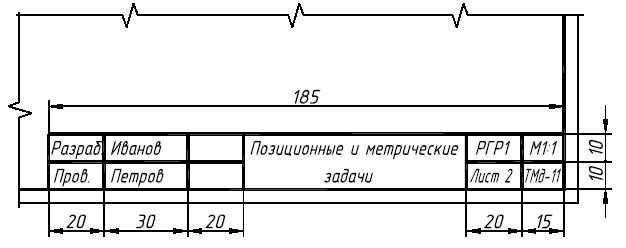
Рис. 1. Упрошенная основная надпись
Все надписи на чертежах выполняются чертежным шрифтом.

Графическая работа №1.
Задача №1.
Через точку D провести перпендикуляр к плоскости, заданной плоской фигурой и найти точку пересечения перпендикуляра с плоскостью.
Данные для своего варианта взять из таблицы 1 по последней цифре зачетной книжки.
Таблица 1
Данные к задаче № 1
| Номер варианта | XA | YA | XB | YB | XC | YC | XD | YD |
Методические рекомендации к решению графической работы №1.
1. Построение перпендикуляра к плоскости.
Прямая перпендикулярна плоскости, если ее проекции перпендикулярны одноименным следам плоскости или соответствующим проекциям горизонтали и фронтали. Для того чтобы построить прямую, перпендикулярную к заданной плоскости необходимо сначала построить в плоскости горизонталь и фронталь, а затем провести проекции перпендикуляра под прямым углом к одноименным проекциям горизонтали и фронтали.
Задача на пересечение прямой линии с плоскостью является одной из основных задач начертательной геометрии.
При решении задач на пересечение прямой с плоскостью следует выделить частный случай. Если плоскость занимает проецирующее положение, то одна проекция точки пересечения определяется в пересечении проекции прямой с проецирующим следом плоскости, а другая проекция строится с помощью линии связи.
Пример 1. Через точку D провести перпендикуляр к плоскости, заданной треугольником AВС. Найти точку пересечения перпендикуляра с заданной плоскостью.
|
|
|
|
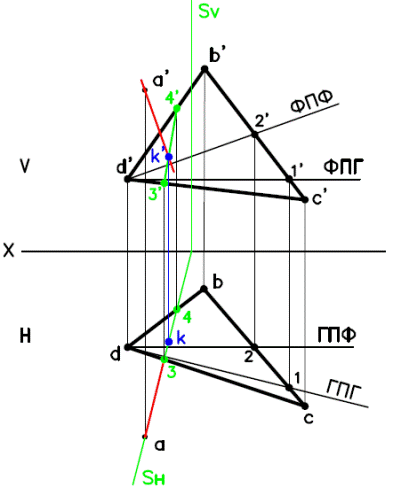
Рис. к примеру 1
Алгоритм решения:
1. В заданной плоскости построить горизонталь и фронталь;
2. Через точку D построить перпендикуляр к соответствующим проекциям фронтали и горизонтали;
3. Через построенный перпендикуляр провести горизонтально (или фронтально) проецирующую плоскость S;
4. построить линию пересечения заданной плоскости и вспомогательной плоскости S (проекции линии пересечения – 3-4, 3’-4’);
5. определить искомую точку К (две ее проекции k, k’) пересечения перпендикуляра с линией пересечения плоскостей (линия 3’-4’).
Задача № 2.
Определить натуральную величину и углы при вершинах треугольника, угол наклона его к плоскости проекции и расстояние от точки D до плоскости многоугольника. Задачу решить методом замены плоскостей или плоскопараллельного перемещения. Данные взять из таблицы 1.
2.Определение размеров фигур.
Существуют следующие способы преобразования проекций:
1. способ замены плоскостей проекций;
2. способ вращения (частный случай – способ плоско-параллельного перемещения).
Эти способы предназначены для решения метрических задач, связанных с определением действительных размеров и формы изображенных на эпюре геометрических объектов, но и не только для решения метрических задач, но и для решения позиционных задач, связанных с построением пересечений геометрических объектов.
Решение многих задач начертательной геометрии значительно упрощается, если заданные геометрические элементы занимают в пространстве частное положение, поэтому в основе способов преобразования проекций – переход от общего положения к частному, когда величина и форма объекта проецируется без искажения.
Основными преобразованиями являются такие, в результате которых прямая линия общего положения становится прямой уровня или проецирующей. Плоскость общего положения преобразуется в проецирующую или плоскость уровня. Так как при этом конечный результат преобразований должен давать решение поставленной задачи.
Если взять плоскость общего положения, то она на каждую плоскость проекций проецируется искаженно и размеры ее будут меньше натуральных, по эпюру мы не можем судить о размерах нашей заданной плоскости.
Принцип ортогональности – плоскости проекций должны быть взаимно перпендикулярны.
Пример 2. Пример решения задачи на определение размеров фигуры методом замены плоскостей проекций.
Задан плоский треугольник АВС и точка D общего положения. Определить на основе метода замены плоскостей проекций, действительную форму и размеры заданной фигуры. А также определить расстояние от точки D до плоскости фигуры.
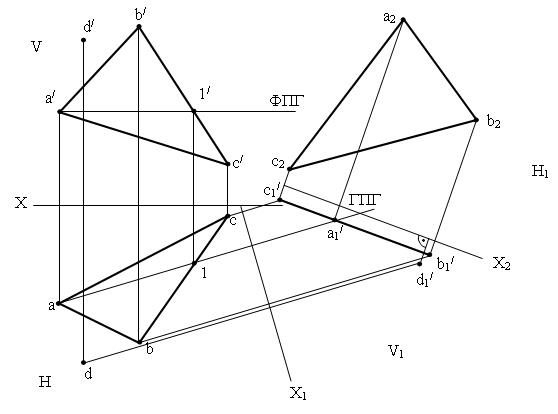
Рис. к примеру 2
Алгоритм решения задачи:
1) необходимо провести горизонталь или фронталь в заданной плоскости ABC. К примеру, чертим горизонталь.
2) перпендикулярно ГПГ построим дополнительную ось Х1 и перемещаем фронтальную плоскость проекций таким образом, чтоб заданная плоскость ABC оказалась бы проецирующей (перпендикулярной) по отношению к новому положению плоскостей проекций, в данном случае к фронтальной плоскости V1.
3) От оси Х1 откладываем расстояния от точек а/, b/, c/ до оси Х на соответствующих проекционных линиях связи. Получим проекции точек треугольника во фронтальной плоскости V1 - а/1, b/1, c/1. Проекция треугольника, построенного по данным точкам, получается в виде прямого отрезка, а значит она перпендикулярна плоскости V1.
4) Параллельно проекции а/1, b/1, c/1 строим дополнительную ось Х2 и изменяем положение плоскостей проекций таким образом, что бы заданная плоскость АВС оказалась бы параллельна какой - либо плоскости проекций, в данном случае горизонтальной плоскости Н1.
5) От оси Х2 откладываем расстояния между точками а , b, c и осью Х1. По полученным проекциям точек а2, b2, c2 строим треугольник. Размеры и форма полученного треугольника а2, b2, c2 являются действительными, истинными.
6) Расстояние от точки D до плоскости АВС определяется кротчайшим расстоянием – перпендикуляром, от проекции точки d1/ до проекции треугольника а/1, b/1, c/.
Пример 3. Пример решения задачи на определение размеров фигур методом плоскопараллельного перемещения объекта.
Задан плоский треугольник АВС и точка D общего положения. Определить на основе метода плоскопараллельного перемещения объекта, действительную форму и размеры заданной фигуры. А также определить расстояние от точки D до плоскости фигуры.
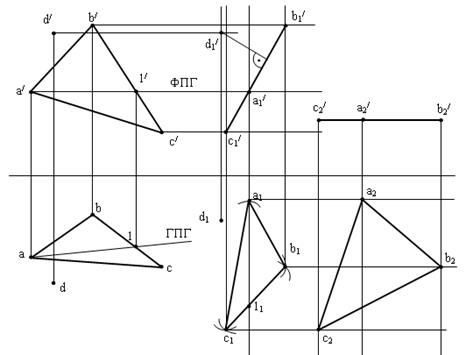
Рис. к примеру 3
Алгоритм построения:
1) необходимо провести горизонталь или фронталь в заданной плоскости ABC. К примеру, чертим горизонталь.
2) повернём горизонтальную проекцию треугольника вместе с ГПГ перпендикулярно оси Х.
3) затем определяем фронтальную проекцию треугольника относительно данного положения треугольника a1 b1 c1. Получим проекцию a1/ b1/ c1/.
4) затем поворачиваем фронтальную проекцию треугольника a1/ b1/ c1/ параллельно горизонтальной плоскости. Относительно данной фронтальной проекции определяем горизонтальную проекцию треугольника a2 b2 c2. Полученная проекция треугольника имеет натуральную форму и размеры треугольника АВС.
5) расстояние от точки D до треугольника АВС определяется кратчайшим расстоянием (перпендикуляром) между фронтальной проекцией точки d1/ и фронтальной проекцией треугольника a1/ b1/ c1/.
Сущность способа плоскопараллельного перемещения:
Плоскости проекций остаются неподвижными, а вращается сам объект. При этом, первое перемещение объекта осуществляется таким образом, чтобы он разместился перпендикулярно какой-либо плоскости проекций. А затем, второе перемещение объекта осуществляется таким образом, чтобы он разместился параллельно какой-либо плоскости проекций. Тогда он проецируется на неё в натуральную форму и величину.
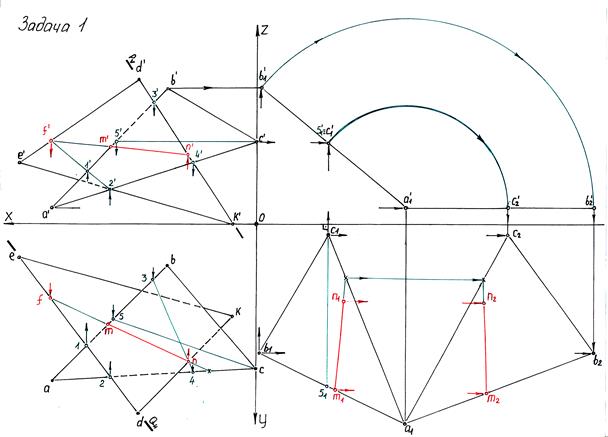
Задача №3
Построить линию пересечения двух треугольников ABC и DEK и показать их видимость. Определить натуральную величину треугольника ABC. Данные для задания взять из таблицы 1.
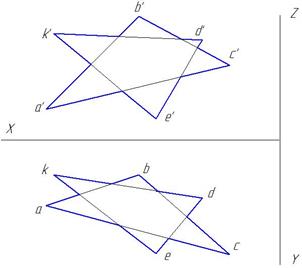
Указания к решению задачи №3
В левой половине листа намечают оси координат и по координатам точек A, B, C, D, E, K из таблицы 1 строят проекции двух треугольников ABC и DEK. Находят линию пересечения треугольников, определяют их видимость. В правой части листа методом плоско-параллельного перемещения, а затем методом вращения определяют натуральную величину треугольника ABC. Затем в нем показывают положение линии пересечения в натуральную величину.
Таблица 2. Данные к задаче 3
| Номер варианта | XА | YА | ZА | XВ | YВ | ZВ | XС | YС | ZС | X Д | Y Д | Z Д | XЕ | YЕ | ZЕ | XК | YК | ZК |
Пример 1 к задаче 3