3.1. F нүктес≥н≥ң жылдамдығын анықтау. F нүктес≥н≥ң жылдамдығын координаттар өстер≥не проекци€лары арқылы анықтаймыз:



2.37-сурет
≈гер  -қа тең болса, онда:
-қа тең болса, онда:


F нүктес≥н≥ң жылдамдығының шамасы:
 .
.
 .
.
3.2. F нүктес≥н≥ң үдеу≥н анықтау. F нүктес≥н≥ң үдеу≥н координаттар өстер≥не проекци€лары арқылы анықтаймыз:


≈гер  -қа тең болса, онда:
-қа тең болса, онда:


F нүктес≥н≥ң үдеу≥н≥ң шамасы:


3.3. F нүктес≥н≥ң жанама құраушы үдеу≥н анықтау. F нүктес≥н≥ң жанама құраушы үдеу≥ мынадай өрнек арқылы анықталады:
 .
.
≈гер  -қа тең болса, онда:
-қа тең болса, онда:
3.4. F нүктес≥н≥ң нормаль құраушы үдеу≥н анықтау. F нүктес≥н≥ң нормаль құраушы үдеу≥ мынадай өрнек арқылы анықталады:

3.5. F нүктес≥н≥ң қисықтық радиусын анықтау. F нүктес≥н≥ң қисықтық радиусы мынадай өрнек арқылы анықталады:

ћеханизм нүктелер≥н≥ң жылдамдықтарын және буындарының бұрыштық жылдамдықтарын жылдамдықтар лезд≥к центр≥ тәс≥л≥мен анықтау.
4.1. ћеханизм нүктелер≥н≥ң жылдамдықтарын анықтау. ћеханизмн≥ң орнын бер≥лген  бұрышына сәйкес тұрғызамыз (
бұрышына сәйкес тұрғызамыз ( ) (2.34-сурет).
) (2.34-сурет).  буыны қозғалмайтын
буыны қозғалмайтын  центр≥н
центр≥н 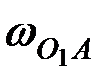 бағытында айнала қозғалады, сондықтан:
бағытында айнала қозғалады, сондықтан:
 ,
, 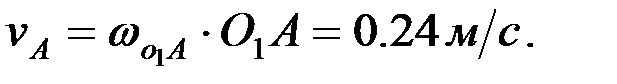

2.38-сурет
ћеханизм нүктелер≥н≥ң жылдамдықтарын анықтау.
∆ылжыма ¬- ның қозғалысы түзу сызықты болғандықтан, жылжыманың жылдамдық векторы, қозғалыс бағытымен бағыттас болады.
 буынының жылдамдықтар лезд≥к центр≥
буынының жылдамдықтар лезд≥к центр≥  , ¬ және ј нүктелер≥ арқылы жүрг≥з≥лген жылдамдық векторларына перпендикул€р түзулерд≥ң қиылысу нүктес≥ болады, ал F нүктес≥н≥ң жылдамдық векторы
, ¬ және ј нүктелер≥ арқылы жүрг≥з≥лген жылдамдық векторларына перпендикул€р түзулерд≥ң қиылысу нүктес≥ болады, ал F нүктес≥н≥ң жылдамдық векторы  кес≥нд≥с≥не перпендикул€р бағытта бағыталады.
кес≥нд≥с≥не перпендикул€р бағытта бағыталады.
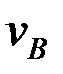 және
және  шамаларын мынадай қатынастар арқылы анықтаймыз:
шамаларын мынадай қатынастар арқылы анықтаймыз:

 ,
,


∆ылдамдықтар лезд≥к центр≥нен нүктелерге дей≥нг≥ ара қашықтық суретте өлшенед≥.
јлдында орындалған амалдарға ұқсас амалдарды орындай отырып, ¬—,  ,
,  буындарыныңсәйкес
буындарыныңсәйкес 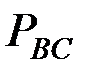 ,
,  ,
,  жылдамдықтар лезд≥к центрлер≥н≥ң орындарын анықтаймыз және
жылдамдықтар лезд≥к центрлер≥н≥ң орындарын анықтаймыз және  ,
,  ,
,  шамаларын мынадай қатынастар арқылы анықтаймыз:
шамаларын мынадай қатынастар арқылы анықтаймыз:
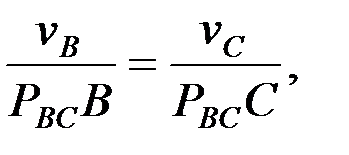





4.2. Ѕуындарының бұрыштық жылдамдықтарын анықтау. ћеханизм буындарының бұрыштық жылдамдықтары мынадай өрнектер арқылы есептелед≥, ал бағыттары нүктелер жылдамдықтарының бағыттарымен анықталады:
|
|
|




ћеханизм нүктелер≥н≥ң жылдамдықтарын және буындарының бұрыштық жылдамдықтарын жылдамдықтар жобасын тұрғызу тәс≥л≥мен анықтау.
5.1. ћеханизм нүктелер≥н≥ң жылдамдықтарын анықтау. Ѕастапқы буын үш≥н ј нүктес≥н≥ң жылдамдығы  формуласы бойынша аналиткалық түрде анықталады. ћеханизмн≥ң қалған нүктелер≥
формуласы бойынша аналиткалық түрде анықталады. ћеханизмн≥ң қалған нүктелер≥  үш≥н жылдамдықтар, векторлық теңдеулерд≥ графикалық жолмен шешу арқылы және ұқсастық ережес≥ бойынша анықталады. ¬ нүктес≥н≥ң жылдамдығын мынадай векторлық теңдеулерд≥ графикалық жолмен шешу арқылы анықтайды:
үш≥н жылдамдықтар, векторлық теңдеулерд≥ графикалық жолмен шешу арқылы және ұқсастық ережес≥ бойынша анықталады. ¬ нүктес≥н≥ң жылдамдығын мынадай векторлық теңдеулерд≥ графикалық жолмен шешу арқылы анықтайды:

 ,
,
мұндағы вектор  шамасы және бағыты жөн≥нен белг≥л≥ (
шамасы және бағыты жөн≥нен белг≥л≥ ( түзу≥не перпендикул€р және
түзу≥не перпендикул€р және  буынының бұрыштық жылдамдығының бағытымен бағыттас);
буынының бұрыштық жылдамдығының бағытымен бағыттас);
вектор  ¬ нүктес≥н≥ң ј¬ буыны ј нүктес≥не қатысты айнала қозғалғандағы жылдамдығы, бағыты ј¬ түзу≥не перпендикул€р, шамасы белг≥с≥з;
¬ нүктес≥н≥ң ј¬ буыны ј нүктес≥не қатысты айнала қозғалғандағы жылдамдығы, бағыты ј¬ түзу≥не перпендикул€р, шамасы белг≥с≥з;
вектор  тоғызыншы т≥рек нүктес≥н≥ң жылдамдығы
тоғызыншы т≥рек нүктес≥н≥ң жылдамдығы 
вектор  ¬ нүктес≥н≥ңт≥рекке қатысты салыстырмалы жылдамдығы, бағыты
¬ нүктес≥н≥ңт≥рекке қатысты салыстырмалы жылдамдығы, бағыты  түзу≥ бойымен сәйкес, шамасы белг≥с≥з;
түзу≥ бойымен сәйкес, шамасы белг≥с≥з;
вектор  ¬ нүктес≥н≥ң ≥здел≥н≥п отырған жылдамдығы, бағыты
¬ нүктес≥н≥ң ≥здел≥н≥п отырған жылдамдығы, бағыты  түзу≥ бойымен бағыттас, шамасы белг≥с≥з.
түзу≥ бойымен бағыттас, шамасы белг≥с≥з.
∆ылдамдықтар жобасын төмендег≥ тәрт≥п бойынша тұрғызамыз:
б≥р≥нш≥ теңдеуге сәйкес жобаның полюс≥нен (ерк≥н алынған p нүктес≥) бастап,  түзу≥не перпендикул€р, жобада ј нүктес≥н≥ң жылдамдығы үш≥н, ұзындығы 24 мм Цтең, ра кес≥нд≥с≥н саламыз;
түзу≥не перпендикул€р, жобада ј нүктес≥н≥ң жылдамдығы үш≥н, ұзындығы 24 мм Цтең, ра кес≥нд≥с≥н саламыз;
а нүктес≥нен ј¬ түзу≥не перпендикул€р  жылдамдығының бағытын саламыз;
жылдамдығының бағытын саламыз;
ек≥нш≥ векторлық теңдеуге сәйкес  болғандықтан, жобаның полюс≥нен
болғандықтан, жобаның полюс≥нен  ке параллель бағытта
ке параллель бағытта 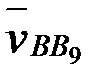 жылдамдығының бағытын саламыз. —онымен, ¬ нүктес≥н≥ң жылдамдық соңы болатын b нүктес≥н табамыз.
жылдамдығының бағытын саламыз. —онымен, ¬ нүктес≥н≥ң жылдамдық соңы болатын b нүктес≥н табамыз.  және
және  кес≥нд≥лер≥
кес≥нд≥лер≥  масштабында
масштабында  және
және  жылдамдықтарын кеск≥ндейд≥.
жылдамдықтарын кеск≥ндейд≥.
 нүктелер≥н≥ң жылдамдықтарын мынадай векторлық теңдеулерд≥ графикалық жолмен шешу арқылы анықтайды:
нүктелер≥н≥ң жылдамдықтарын мынадай векторлық теңдеулерд≥ графикалық жолмен шешу арқылы анықтайды:


 ,
, 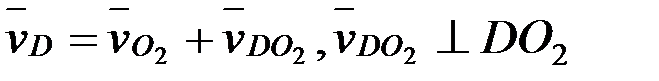 ,
,


 нүктелер≥н≥ң жылдамдықтарының шамаларын анықтау үш≥н жылдамдықтар жобасының масштабын анықтаймыз:
нүктелер≥н≥ң жылдамдықтарының шамаларын анықтау үш≥н жылдамдықтар жобасының масштабын анықтаймыз:
 ,
, 
—онда:



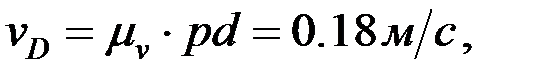

F нүктес≥н≥ң жылдамдығын ұқсастық ережес≥ бойынша анықтайды:

5.2. Ѕұрыштық жылдамдықтарын анықтау. ћеханизм буындарының бұрыштық жылдамдықтары мынадай өрнектер арқылы есептелед≥:
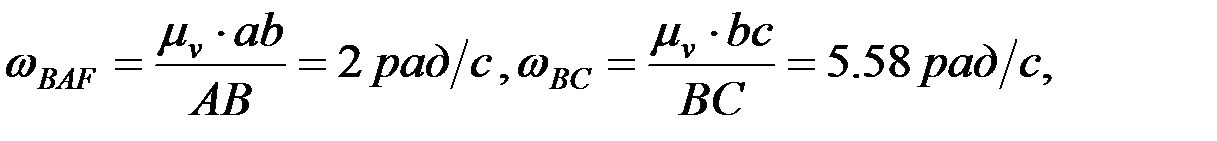


ћеханизм нүктелер≥н≥ң үдеулер≥н және буындарының бұрыштық үдеулер≥н үдеулерд≥ қосу теоремасын (проекци€лық әд≥с) пайдаланып анықтау.
|
|
|
6.1. ћеханизм нүктелер≥н≥ң үдеулер≥н анықтау. ¬ нүктес≥н≥ң толық үдеу≥н, мына формуланы қолдану арқылы табамыз:
 ,
,

2.39-сурет
мұндағывектор  полюс рет≥нде қабылданған нүктен≥ң үдеу≥, шамасы
полюс рет≥нде қабылданған нүктен≥ң үдеу≥, шамасы  , ќ1 айналу центр≥не қарай бағытталады; вектор
, ќ1 айналу центр≥не қарай бағытталады; вектор 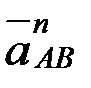 - өске ұмтылғыш үдеу, модул≥
- өске ұмтылғыш үдеу, модул≥  , ј¬ бойымен полюске қарай бағытталады; вектор
, ј¬ бойымен полюске қарай бағытталады; вектор  айналдырушы үдеу, шамасы белг≥с≥з, ј¬- ға перпендикул€р айналыс болатын жаққа қарай бағытталады.
айналдырушы үдеу, шамасы белг≥с≥з, ј¬- ға перпендикул€р айналыс болатын жаққа қарай бағытталады.
¬ нүктес≥н≥ң толық үдеу≥  ны және
ны және  айналдырушы үдеуд≥ табу үш≥н векторлық теңд≥кт≥ң ек≥ жағында координаттар өстер≥не проекци€лаймыз:
айналдырушы үдеуд≥ табу үш≥н векторлық теңд≥кт≥ң ек≥ жағында координаттар өстер≥не проекци€лаймыз:
 ,
,
 .
.
ќсы соңғы теңд≥ктерд≥ң көмег≥мен, ≥здеп отырған үдеулерд≥ табамыз:


 буынының бұрыштық үдеу≥:
буынының бұрыштық үдеу≥:  .
.
F нүктес≥н≥ң толық үдеу≥н, мына формуланы қолдану арқылы табамыз:

мұндағывектор 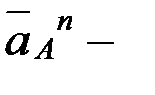 полюс рет≥нде қабылданған нүктен≥ң үдеу≥, шамасы
полюс рет≥нде қабылданған нүктен≥ң үдеу≥, шамасы  , ќ1 айналу центр≥не қарай бағытталады. вектор
, ќ1 айналу центр≥не қарай бағытталады. вектор  - өске ұмтылғыш үдеу, модул≥
- өске ұмтылғыш үдеу, модул≥  , ј¬ бойымен полюске қарай бағытталады. Үш≥нш≥ вектор
, ј¬ бойымен полюске қарай бағытталады. Үш≥нш≥ вектор  айналдырушы үдеу, модул≥
айналдырушы үдеу, модул≥
 .
.
јлдыңғы векторлық теңд≥кт≥ң ек≥ жағында  бойымен бағытталған өске және оған перпендикул€р өске проекци€лаймыз:
бойымен бағытталған өске және оған перпендикул€р өске проекци€лаймыз:
.
ќсыдан:


— нүктес≥н≥ң толық үдеу≥н, мына формулаларды қолдану арқылы табамыз:


мұндағывектор  полюс рет≥нде қабылданған нүктен≥ң үдеу≥, шамасы
полюс рет≥нде қабылданған нүктен≥ң үдеу≥, шамасы  ; вектор
; вектор  - өске ұмтылғыш үдеу, шамасы
- өске ұмтылғыш үдеу, шамасы  , ¬— бойымен полюске қарай бағытталады; вектор
, ¬— бойымен полюске қарай бағытталады; вектор 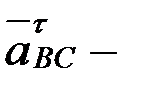 айналдырушы үдеу, шамасы
айналдырушы үдеу, шамасы  белг≥с≥з; вектор
белг≥с≥з; вектор  өске ұмтылғыш үдеу, шамасы
өске ұмтылғыш үдеу, шамасы  ќ2 айналу центр≥не қарай бағытталады; вектор
ќ2 айналу центр≥не қарай бағытталады; вектор  айналдырушы үдеу, шамасы белг≥с≥з,
айналдырушы үдеу, шамасы белг≥с≥з,  - ға перпендикул€р айналыс болатын жаққа қарай бағытталады.
- ға перпендикул€р айналыс болатын жаққа қарай бағытталады.
јлдыңғы векторлық теңд≥кт≥ң ек≥ жағында координаттар өстер≥не проекци€лаймыз:

 .
.
ќсыдан:

 ,
, 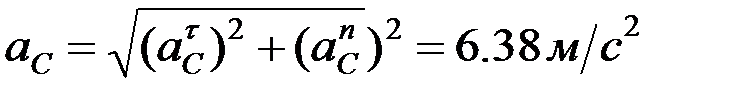 .
.
¬— және ќ2—D буындарының бұрыштық үдеулер≥ мынадай өрнектер арқылы есептелед≥:
 ,
,  .
.
D нүктес≥н≥ң толық үдеу≥н, мына формуланы қолдану арқылы табамыз:
 ,
,
мұндағы вектор 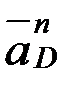 - өске ұмтылғыш үдеу, шамасы
- өске ұмтылғыш үдеу, шамасы 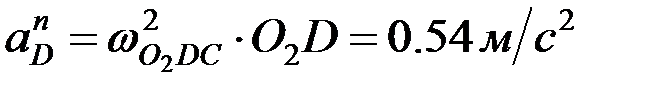 ,
,  бойымен айналу центр≥не қарай бағытталады, ал вектор
бойымен айналу центр≥не қарай бағытталады, ал вектор  айналдырушы үдеу, шамасы
айналдырушы үдеу, шамасы  . D нүктес≥н≥ң толық үдеу шамасы:
. D нүктес≥н≥ң толық үдеу шамасы:
.
≈ нүктес≥н≥ң толық үдеу≥н, мына формуланы қолдану арқылы табамыз:
 ,
,
мұндағывекторлар 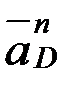 .
.  шамалары және бағыттары жөн≥нен белг≥л≥; вектор
шамалары және бағыттары жөн≥нен белг≥л≥; вектор 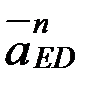 - өске ұмтылғыш үдеу, шамасы
- өске ұмтылғыш үдеу, шамасы 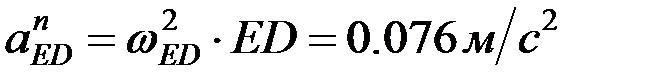 , ED бойымен полюске қарай бағытталады; вектор
, ED бойымен полюске қарай бағытталады; вектор  айналдырушы үдеу, шамасы
айналдырушы үдеу, шамасы  белг≥с≥з,
белг≥с≥з,  - ға перпендикул€р айналыс болатын жаққа қарай бағытталады. јлдыңғы векторлық теңд≥кт≥ң ек≥ жағында координаттар өстер≥не проекци€лаймыз:
- ға перпендикул€р айналыс болатын жаққа қарай бағытталады. јлдыңғы векторлық теңд≥кт≥ң ек≥ жағында координаттар өстер≥не проекци€лаймыз:

 .
.
ќсыдан:
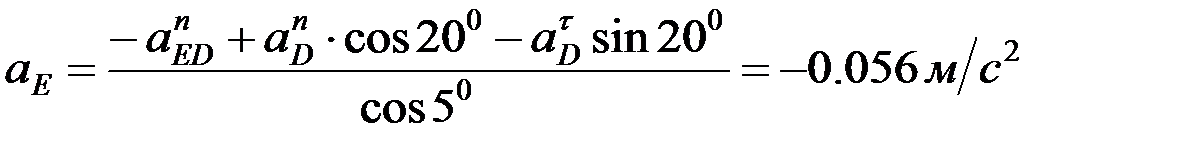 ,
,
 .
.
6.2. Ѕуындарының бұрыштық үдеулер≥н анықтау. ћеханизм буындарының бұрыштық үдеулер≥ мынадай өрнектер арқылы есептелед≥:
 ,
,  ,
,
 ,
,  .
.
ћеханизм нүктелер≥н≥ң үдеулер≥н және буындарының бұрыштық үдеулер≥н үдеулер жобасын тұрғызу тәс≥л≥мен анықтау.
|
|
|
7.1. ћеханизм нүктелер≥н≥ң үдеулер≥н анықтау. Үдеулер жобасын  болатынын ескере отырып тұрғызамыз. Ѕастапқы буын үш≥н ј нүктес≥н≥ң үдеу≥
болатынын ескере отырып тұрғызамыз. Ѕастапқы буын үш≥н ј нүктес≥н≥ң үдеу≥  формуласы бойынша аналитикалық түрде анықталады. ћеханизмн≥ң қалған нүктелер≥
формуласы бойынша аналитикалық түрде анықталады. ћеханизмн≥ң қалған нүктелер≥  үш≥н үдеулер≥, векторлық теңдеулерд≥ графикалық жолмен шешу арқылы және ұқсастық ережес≥ бойынша анықталады. ¬ нүктес≥н≥ң үдеу≥н мынадай векторлық теңдеулерд≥ графикалық жолмен шешу арқылы анықтайды:
үш≥н үдеулер≥, векторлық теңдеулерд≥ графикалық жолмен шешу арқылы және ұқсастық ережес≥ бойынша анықталады. ¬ нүктес≥н≥ң үдеу≥н мынадай векторлық теңдеулерд≥ графикалық жолмен шешу арқылы анықтайды:
 ,
, 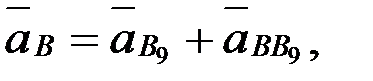 ,
,
мұндағывектор  полюс рет≥нде қабылданған нүктен≥ң үдеу≥, шамасы
полюс рет≥нде қабылданған нүктен≥ң үдеу≥, шамасы  , ќ1ј- ға параллель; вектор
, ќ1ј- ға параллель; вектор  өске ұмтылғыш үдеу, шамасы
өске ұмтылғыш үдеу, шамасы  , ј¬- ға параллель; вектор
, ј¬- ға параллель; вектор  айналдырушы үдеу, шамасы белг≥с≥з, ј¬- ға перпендикул€р; вектор
айналдырушы үдеу, шамасы белг≥с≥з, ј¬- ға перпендикул€р; вектор  т≥ректе жататын нүктес≥н≥ң үдеу≥, шамасы
т≥ректе жататын нүктес≥н≥ң үдеу≥, шамасы  ; вектор
; вектор  ¬ нүктес≥н≥ң т≥реке қатысты салыстырмалы үдеу≥, шамасы белг≥с≥з, xx- ке параллель.
¬ нүктес≥н≥ң т≥реке қатысты салыстырмалы үдеу≥, шамасы белг≥с≥з, xx- ке параллель.
Үдеулер жобасын мынадай тәрт≥п бойынша тұрғызамыз:
б≥р≥нш≥ векторлық теңдеуге сәйкес жобаның полюс≥нен (ерк≥н алынған  нүктес≥) бастап,
нүктес≥) бастап,  түзу≥не параллель, жобада ј нүктес≥н≥ң үдеу≥ үш≥н, ұзындығы 6 мм Цге тең,
түзу≥не параллель, жобада ј нүктес≥н≥ң үдеу≥ үш≥н, ұзындығы 6 мм Цге тең,  а кес≥нд≥с≥н саламыз;
а кес≥нд≥с≥н саламыз;
а нүктес≥нен ј¬ түзу≥не параллель 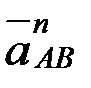 үдеу≥н кеск≥ндейт≥н ұзындығы мынадай теңд≥кпен анықталатын
үдеу≥н кеск≥ндейт≥н ұзындығы мынадай теңд≥кпен анықталатын 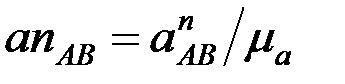 кес≥нд≥с≥н саламыз;
кес≥нд≥с≥н саламыз;
 нүктес≥нен ј¬ түзу≥не перпендикул€р түзу саламыз;
нүктес≥нен ј¬ түзу≥не перпендикул€р түзу саламыз;
ек≥нш≥ векторлық теңдеуге сәйкес жобаның полюс≥нен бастап хх түзу≥не параллель түзу саламыз. ќсы түзу  нүктес≥нен ј¬ түзу≥не перпендикул€р түзумен
нүктес≥нен ј¬ түзу≥не перпендикул€р түзумен  нүктес≥нде қиылысады.
нүктес≥нде қиылысады.  ,
, 
 ,
,  ,
,  , кес≥нд≥лер≥
, кес≥нд≥лер≥  масштабында
масштабында  ,
, 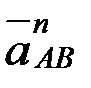 ,
,  ,
,  үдеулер≥н кеск≥ндейд≥.
үдеулер≥н кеск≥ндейд≥.
 нүктелер≥н≥ң үдеулер≥н мынадай векторлық теңдеулерд≥ графикалық жолмен шешу арқылы анықтайды:
нүктелер≥н≥ң үдеулер≥н мынадай векторлық теңдеулерд≥ графикалық жолмен шешу арқылы анықтайды:


.
 нүктелер≥н≥ң үдеулер≥н≥ң шамаларын анықтау үш≥н, үдеулер жобасының масштабын анықтаймыз:
нүктелер≥н≥ң үдеулер≥н≥ң шамаларын анықтау үш≥н, үдеулер жобасының масштабын анықтаймыз:
 ,
,  .
.
—онда:
 ,
,  ,
, 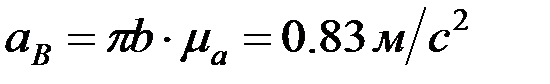 .
.
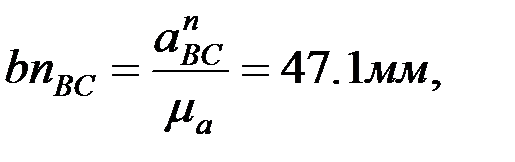
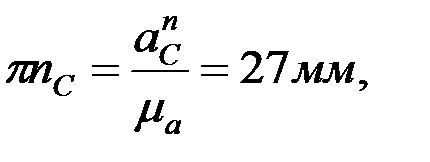


F және D нүктелер≥н≥ң үдеулер≥н ұқсастық ережес≥ бойынша анықтайды:

 ,
,
 ,
,

 ,
,  .
.
7.2. Ѕұрыштық үдеулер≥н анықтау. ћеханизм буындарының бұрыштық үдеулер≥ мынадай өрнектер арқылы есептелед≥:

 ,
,
 ,
,  .
.
8. улисалы механизм F нүктес≥н≥ң абсолют жылдамдығының ж≥не үдеу≥н≥ң құраушыларын анықтау.
9. улисалы механизм буынының бұрыштық жылдамдығын, бұрыштық үдеу≥н электронды есептеу машинасының көмег≥мен анықтау. улисаның  нүктес≥н≥ң абсолют жылдамдығы белг≥л≥:
нүктес≥н≥ң абсолют жылдамдығы белг≥л≥:

 .
.
∆ылдамдықтарды қосу теоремасы бойынша:
 .
.
—алыстырмалы жылдамдығы  түзу≥ бойымен, ал тасымал жылдамдығы осы түзуге перпендикул€р бағытталған. ƒиагонал≥
түзу≥ бойымен, ал тасымал жылдамдығы осы түзуге перпендикул€р бағытталған. ƒиагонал≥  нүктес≥н≥ң жылдамдығы
нүктес≥н≥ң жылдамдығы  , ал қабырғалары
, ал қабырғалары  ,
,  болатын параллелограм тұрғызамыз.
болатын параллелограм тұрғызамыз.
—уретте өлшеу арқылы алатынымыз:


улисаның тасымал бұрыштық жылдамдығы мынадай өрнек арқылы анықталады:

 нүктес≥н≥ң абсолют үдеу≥ салыстырмалы, тасымал және кориолис үдеулер≥н≥ң геометри€лық қосындысына тең:
нүктес≥н≥ң абсолют үдеу≥ салыстырмалы, тасымал және кориолис үдеулер≥н≥ң геометри€лық қосындысына тең:
|
|
|
 ,
,
мұндағы вектор 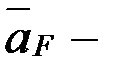 абсолют үдеу, шамасы
абсолют үдеу, шамасы  ; вектор
; вектор  салыстырмалы жанама құраушы үдеу, шамасы белг≥с≥з; вектор
салыстырмалы жанама құраушы үдеу, шамасы белг≥с≥з; вектор  салыстырмалы нормаль құраушы үдеу, шамасы
салыстырмалы нормаль құраушы үдеу, шамасы  ;
;
вектор  тасымал жанама құраушы үдеу, шамасы белг≥с≥з; вектор
тасымал жанама құраушы үдеу, шамасы белг≥с≥з; вектор  тасымал нормаль құраушы үдеу, шамасы
тасымал нормаль құраушы үдеу, шамасы  ; вектор
; вектор  кориолис үдеу≥, шамасы
кориолис үдеу≥, шамасы  .
.
јлдыңғы векторлық теңд≥кт≥ң ек≥ жағында координаттар өстер≥не проекци€лаймыз:

 .
.
ќсыдан:

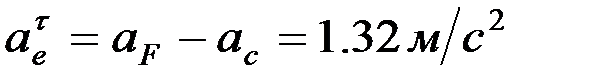 ,
, 
9. улисалы механизм буынының бұрыштық жылдамдығын, бұрыштық үдеу≥н электронды есептеу машинасының көмег≥мен анықтау. улисалы механизмн≥ң кез келген орны үш≥н мынадай векторлық теңд≥ктерд≥ құрамыз:



немесе 
“еңд≥ктерд≥ң ек≥ жағында координаттар өстер≥не проекци€лаймыз:


 .
.
”ақыт бойынша ек≥ рет дифференциалдаймыз. Ѕ≥р рет дифференциалдасақ бұрыштық жылдамдық  және салыстырмалы жылдамдық
және салыстырмалы жылдамдық  ге қатысты алгебралық теңдеулерд≥ аламыз:
ге қатысты алгебралық теңдеулерд≥ аламыз:





2.40-сурет
≈к≥нш≥ рет дифференциалдасақ бұрыштық үдеу  және салыстырмалы үдеу
және салыстырмалы үдеу  ге қатысты алгебралық теңдеулерд≥ аламыз:
ге қатысты алгебралық теңдеулерд≥ аламыз:


≈к≥нш≥ рет дифференциалдасақ, бұрыштық үдеу  және салыстырмалы үдеу
және салыстырмалы үдеу  ге қатысты алгебралық теңдеулерд≥ аламыз:
ге қатысты алгебралық теңдеулерд≥ аламыз:


≈к≥ теңдеулер жүйес≥н  және
және  ге қатысты шешем≥з:
ге қатысты шешем≥з:
 (
( )
)
 ,
,
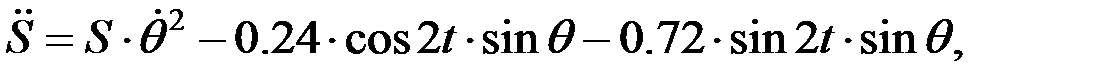 (
(
 )
)
 .
.
ѕрограмманы жазу
Ё≈ћ көмег≥мен  және
және  теңдеулер жүйес≥н шешем≥з. Қадамы басылым қадамына тең Ёйлер әд≥с≥н пайдаланамыз.
теңдеулер жүйес≥н шешем≥з. Қадамы басылым қадамына тең Ёйлер әд≥с≥н пайдаланамыз.  уақытқа байланысты қадам,
уақытқа байланысты қадам,  интеграци€ номер≥, мынадай шект≥ аралықта өзгеред≥
интеграци€ номер≥, мынадай шект≥ аралықта өзгеред≥  .
.


 ,
,
 бер≥лген≥н енг≥зу;
бер≥лген≥н енг≥зу;
 (
( ) теңдеулер≥н≥ң шеш≥м≥,
) теңдеулер≥н≥ң шеш≥м≥,  н≥ анықтау;
н≥ анықтау;
 (
( ) теңдеулер≥н≥ң шеш≥м≥,
) теңдеулер≥н≥ң шеш≥м≥,  н≥ анықтау;
н≥ анықтау;
 қорытындыларды печатқа беру;
қорытындыларды печатқа беру;
 егер
егер  болса, онда есептеуд≥ қайталау;
болса, онда есептеуд≥ қайталау;
 жұмыстың соңы.
жұмыстың соңы.
2.3-кесте

| 
| 
| 
| 
| 
| 
| 
| 
|
| 0.0 | 0.0 | 1.1071 | 0.1342 | 1.2000 | -4.1600 | 0.3220 | 0.0859 | |
| 0.2616 | 0.5236 | 1.3282 | 0.2163 | 0.6154 | -1.1069 | 0.2882 | -0.3175 | |
| 0.5236 | 1.0472 | 1.4525 | 0.2775 | 0.4424 | -0.3477 | 0.1677 | -0.5785 | |
| 0.7854 | 1.5708 | 1.5708 | 0.3000 | 0.4000 | 0.0000 | 0.0000 | -0.6720 | |
| 1.0472 | 2.0944 | 1.6791 | 0.2775 | 0.4424 | 0.3478 | -0.1677 | -0.5785 | |
| 1.3090 | 2.6180 | 1.8134 | 0.2163 | 0.6154 | 1.1969 | -0.2882 | -0.3175 | |
| 1.5708 | 3.1416 | 2.0345 | 0.1342 | 1.2000 | 4.1602 | -0.3220 | 0.0859 | |
| 1.8326 | 3.6652 | 2.6180 | 0.0606 | 4.0001 | 20.7848 | -0.2078 | 0.9500 | |
| 2.0944 | 4.1888 | 4.0161 | 0.0468 | 4.1729 | -19.3298 | 0.00714 | 0.2591 | |
| 2.3562 | 4.7124 | 4.7124 | 0.0600 | 2.0000 | 0.0002 | 0.0000 | -0.4800 | |
| 2.6180 | 5.2360 | -0.8745 | 0.0468 | 4.1731 | 10.3304 | -0.0714 | 0.2592 | |
| 2.8798 | 5.7596 | 0.5236 | 0.0600 | 3.9999 | -20.7841 | 0.2079 | 0.9600 | |
| 3.1416 | 6.2832 | 1.1071 | 0.1342 | 1.2000 | -4.1595 | 0.3220 | 0.0859 |
ƒинамика






