Қозғалмайтын өсті айналатын қатты дене нүктелерінің қозғалысын қарастырайық. Мұнадай дененің барлық нүктелерінің қозғалыс кезіндегі траекториялары, жазықтықтары айналу өсіне перпендикуляр, ал центрлері айналу өсінде жататын, концентрлі шеңберлер болады. Дененің айналу өсінен h қашықтықта жатқан кез келген бір нүктесі М -ді алайық. Бұл нүктенің жылдамдығының шамасы:
, (2.76)
| 2.16-сурет |
векторы, радиусы h, центрі О нүктесінде жататын шеңберге жанамамен, айналыс болатын жаққа қарай бағытталады (2.16-сурет).
(2.76)- шы формула нүкте М -нің жылдамдығын геометриялық әдіспен табуға мүмкіндік береді. Ал жылдамдықты векторлық тәсілді қолданып табуға да болады. Ол үшін берілген нүкте М -нің Oxyz өстер жүйесіндегі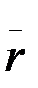 
= 
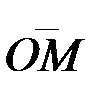радиус-векторын алайық. Осы 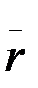және 
векторының векторлық қөбейтіндісін құрайық: 
х 
(2.16 сурет).
Бұл көбейтіндінің модулі
. (2.77)
(2.77)–теңдік, векторлық көбейтіндінің модулі, нүкте жылдамдығының (2.76) формуламен есептелінетін модуліне тең екенін көрсетеді. Осыдан соң 
х 
векторының бағытына тоқтайық. Бұл вектор, үшбұрыш Δ O1MO жазықтығына М -нүктесіне тұрғызылған перпендикуляр бойыменен векторымен бірдей бір жаққа қарай бағытталғанын 2.16-суреттен көруге болады. Сонымен бұл айтылғандардан, екі вектор, 
x 
және 
бір-біріне тең екенін көреміз. Демек мынадай формуланың орынды екені дәлелденеді:
(2.78)
(2.78)–формула қатты дене кинематикасындағы маңызды формула. Бұл формула Эйлер формуласы деп аталады.
Дененің кез келген нүктесі М, радиусы h = О1М және жазықтығы айналу өсіне перпендикуляр орналасқан, шеңбер сыза отырып қозғалады дедік. Демек бұл нүктенің толық үдеуін екі құраушыға жіктеу арқылы анықтай аламыз (2.17-сурет). Шенбер бойымен қозғалған нүктенің жанама үдеуі:
, (2.79)
және оның нормальүдеуі:
. (2.80)
| 2.17-сурет |
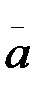-векторын құраушылары 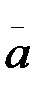τ және 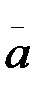n арқылы анықтау мына формулалар арқылы жүргізіледі:
, (2.81)
. (2.82)
Егер 
векторының модулі | |=const болып, оның бағыты ғана уақыт өсуіне қарай өзгеретін болса, онда (2.78)-формуладан мынадай теңдік алынады:
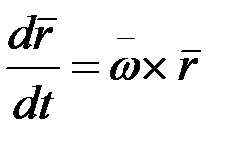. (2.83)
Бұл теңдіктегі 
радиус-вектор -дің бұрылуының бұрыштық жылдамдығы. Енді (2.83) теңдігінің екі жағынан уақыт бойынша туынды алайық:
. (2.84)
(2.84)–теңдіктің оң жағындағы қосылғыш векторларды жеке-жеке қарастырайық. Ондағы бірінші қосылғыш вектор модулі М -нүктесінің жанама үдеуіне тең:
. (2.85)
(2.85)–тің оң жағындағы бірінші вектор, М- нүктесіндегі жылдамдық векторы 
мен бағыттас. Демек, бұдан:
. (2.86)
Ал енді ондағы екінші қосылғыш вектордың модулі:
. (2.87)
Бұл вектор МО1 түзуінің бойымен О1 центріне қарай, айналу өсіне перпендикуляр бағытталады. Демек
. (2.88)
Сонымен (2.80) – (2.82) формулаларын векторлық тәсілді қолданып та алуға болатынын көрсеттік.
1-мысал: Атанаққа оралған жіпке ілінген жүк A, атанақты айналмалы қозғалысқа келтіре отырып, тыныштық қалпынан бірқалыпты үдемелі төменгі бағытта қозғалады. Атанақ бірінші 3 сек арлығында 9 айналым жасайды. Атанақтың диаметрі 
см.
Атанақ бетіндегі нүктенің 5сек уақыт мезгіліндегі жылдамдығын және үдеуін табу керек (14-сурет).
а) б)
2.18-сурет.
Шешуі. Атанақтың бірқалыпты айнымалы айналмалы қозғалыс теңдеуін жазамыз:
. (1)
Бұрыштық жылдамдықтың айналу өсіндегі проекциясы айналу бұрышы (1)-ден уақыт бойынша алынған туындыға тең:
. (2)
Бастапқы мәндері: j0=0, w0=0. Осы шарттарды ескере отырып (1) және (2) - теңдеулерді мына түрде жазамыз:
, (3)
. (4)
t = 3 с уақыт мезгілін де j = 9 айналыс болғандықтан, (3) – теңдеуден бұрыштық үдеу e - ді табамыз:
.
(4)–теңдеуден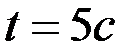 
мезгіліндегі атанақтың бұрыштық жылдамдығы 
-ны табамыз:
.
Атанақтың бетіндегі B нүктесінің (14,б-сурет) сызықтық жылдамдығын, жанама және нормаль құраушы үдеулерін осы уақыт мезгілінде анықтаймыз:
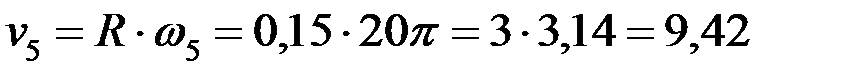м/с,
м/с2,
м/с2.
Атанақтың бетіндегі нүктенің толық үдеуінің модулі:
м/с2.
Жүктің жылдамдығы атанақтың бетіндегі нүктенің сызықтық жылдамдығына тең:
м/с.
Жүктің үдеуі атанақтың бетіндегі нүктенің жанама құраушы үдеуіне тең:
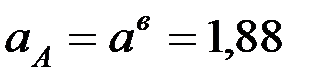м/с2.
2-мысал: Раиусы 
тістегеріш 1-ге отырғызылған радиусы r валды жүк В айналмалы қозғалысқа келтіреді. Жүк тыныштық қалпынан қозғалып бастайды және тұрақты 
үдеумен қозғалады. Тістегеріш 1-мен іліністе болатын радиусы r2 тістегеріш 2-нің қозғалыс заңдылығын табу керек.
Шешуі. Жүк В (15-сурет) бастапқы жылдамдықсыз тұрақты 
үдеумен қозғалып бастайды, сондықтан, кез келген мезгілінде 
болады. Валдың бетіндегі нүкте жылдамдығы осы жылдамдыққа және w1 r -ге тең. Сондықтан:
| 2.19-сурет |
.
w2-ні табамыз. Іліністегі нүкте С -ның сызықтық жылдамдығы екі тістегерішке ортақ:
,
осыдан
.
Осы теңдіктің екі жағында 
-ға көбейтіп алу арқылы, мынадай теңдік аламыз:
.
Бұны 0-ден j2 -ге және 0-ден t -ға дейінгі шектерде интегралдай отырып, тістегеріш 2-нің бірқалыпты айнымалы айналмалы қозғалыс заңдылығын табамыз:
