Текстова задача - це словесна модель деякого явища (ситуації, процесу). Щоб вирішити таке завдання, треба перевести її на мову математичних дій, тобто побудувати її математичну модель.
Рішення будь-якої задачі - процес складної розумової діяльності. Реальні об'єкти і процеси в задачі бувають настільки багатогранні і складні, що кращим способом їх вивчення часто є побудова та дослідження моделі як потужного знаряддя пізнання. Вирішенню текстових завдань у навчанні приділяється величезна увага. Пов'язано це з тим, що такі завдання часто є не тільки засобом формування багатьох математичних понять, але і головне - засобом формування вмінь будувати математичні моделі реальних явищ, а також засобом розвитку мислення дітей. Існують різні методичні підходи до навчання дітей рішенню текстових завдань. Але яку б методику навчання ні вибрав вчитель, йому треба знати, як побудовані такі завдання.
Будь-яка текстова завдання являє собою опис якого-небудь явища (ситуації, процесу). З цієї точки зору текстова задача є словесна модель явища (ситуації, процесу). І, як у будь моделі, в текстовій завданню описується не все явище в цілому, а лише деякі його боку, головним чином, його кількісні характеристики. Узагальнюючи, можна сказати, що текстова завдання є опис на природній мові деякого явища (ситуації, процесу) з вимогою дати кількісну характеристику будь-якого компонента цього явища, встановити наявність або відсутність деякого відносини між компонентами або визначити вид цього відношення.
Рішення будь-якої задачі - процес складної розумової діяльності. Щоб оволодіти ним, треба знати основні етапи рішення задачі і деякі прийоми їх виконання.
Діяльність по вирішенню завдання арифметичним методом включає наступні основні етапи:
1. Аналіз завдання.
2. Пошук плану рішення задачі.
3. Здійснення плану рішення задачі.
4. Перевірка рішення задачі.
У реальному процесі вирішення завдання названі етапи не мають чітких меж і не завжди виконуються однаково повно. Все залежить від рівня знань і умінь вирішального.
1. Аналіз завдання
Основне призначення цього етапу - зрозуміти в цілому ситуацію, описану в задачі; виділити умови і вимоги; назвати відомі і шукані об'єкти, виділити всі відносини (залежності) між ними. Роблячи аналіз завдання, виокремлюючи її умови, ми повинні співвідносити цей аналіз з вимогами завдання. І таблиця, і схематичне креслення є допоміжними моделями завдання. Вони служать формою фіксації аналізу текстової задачі і є основним засобом пошуку плану її вирішення.
Після побудови допоміжної моделі необхідно перевірити:
1) чи всі об'єкти завдання показані на моделі?
2) чи всі відносини між об'єктами відображені?
3) чи всі числові дані наведені?
4) чи є питання (вимога) і чи правильно він вказує шукане?
2. Пошук і складання плану виконання завдання.
Призначення цього етапу: встановити зв'язок між даними і вихідними об'єктами, намітити послідовність дій. План рішення задачі - це лише ідея рішення, його задум. Пошук плану рішення задачі є важким процесом. Одним з найбільш відомих прийомів пошуку плану виконання завдання арифметичним способом є розбір завдання по тексту або за її допоміжної моделі. Розбір задачі проводиться у вигляді ланцюжка міркувань, яка може починатися від даних завдання, так і від її питань.
3. Здійснення плану рішення задачі
Призначення даного етапу - знайти відповідь на вимогу завдання,
виконавши всі дії відповідно до плану. Для текстових завдань, що вирішуються арифметичним способом, використовуються такі прийоми: запис дій (з поясненням, без пояснення, з питаннями); запис у вигляді виразу.
4. Перевірка рішення задачі
Призначення даного етапу - встановити правильність або помилковість виконання рішення.
Навчання із застосуванням моделювання підвищує активність розумової діяльності учнів, допомагає зрозуміти завдання, самостійно знайти раціональний шлях вирішення, встановити потрібний спосіб перевірки, визначити умови, за яких задача має чи не має рішення. Модель дає можливість більш повно побачити залежність між даними і шуканими в задачі, представити задачу в цілому, допомагає узагальнити теоретичні знання. Постановка навчальної задачі становить мотиваційно-орієнтовний ланка - перша ланка навчальної діяльності. Другим (центральним) ланкою навчальної діяльності є виконавське, тобто такі навчальні дії для вирішення навчальної задачі:
1) перетворення умов предметної завдання з метою виявлення в ній основного відносини;
2) моделювання виділеного в ній відносини в предметній, графічній або буквеної формі;
3) перетворення моделі відношення для вивчення його властивостей;
4) побудова системи приватних завдань, що вирішуються загальним способом.
Щоб навчити школярів самостійно і творчо вчитися, потрібно включати їх у спеціально організовану діяльність, зробити господарями цієї діяльності. Одним із способів включення учнів в активну діяльність у процесі вирішення завдань і є моделювання.
Задача. У коробці було 5 зелених кружечків і кілька червоних. Всього 8кружечків. Скільки червоних кружечків було в коробці?
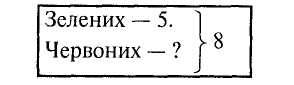
Задача. З першої яблуні зірвали 5 кошиків яблук, а з другої — на 2 більше. Скільки кошиків яблук зірвали з другої яблуні?'(Мал. 116).

Задача. З 14 м полотна пошили 7 наволочок. Скільки таких наволочок можна пошити з 8м полотна?(Табл. 35).
Таблиця 35
| Норма на одну наволочку | Кількість наволочок | Кількість тканини |
| Однакова | 14 м 8 м |






