Лекція №4
Тема: «Технології розвивального навчання»
1.Застосування опорних схем.
2.Моделювання арифметичних дій.
3.Моделювання текстових задач.
4.Моделювання завдань на частини і дроби.
Застосування опорних схем.
В основі технології розвивального навчання лежить уявлення про розвиток дитини як суб’єкта особистої діяльності. Для того щоб навчання було розвивальним, необхідно звернути увагу на побудову уроку.
Організація навчання (етапи уроку):
1) формування в учнів мотивів навчання, позитивного ставлення до нього;
2) оволодіння новою інформацією, що являє собою пізнавальну діяльність школярів, спрямовану на опанування нових знань та способів навчальних дій;
3) відтворення учнями засвоєного матеріалу;
4) формування вмінь та навичок у стандартних і нових умовах;
5) узагальнення знань, умінь та навичок школярів;
6) продуктивна пізнавальна діяльність учнів для формування знань, умінь та навичок на творчому рівні.
Розвивальне навчання – такий процес діяльності учнів, у ході якого кожна дитина повинна самостійно або за допомогою вчителя осмислити матеріал, творчо застосувати його в нестандартних умовах та свідомо запам’ятати для дальшого навчання. При цьому відбувається самовдосконалення та самовираження дитини. Модель розвивального навчання розрахована на вдосконалення розумових процесів з урахуванням можливостей кожної дитини.
Головною метою розвивального навчання є формування активного, самостійного творчого мислення учня і на цій основі поступового переходу в самостійне навчання.
Завдання розвивального навчання: формування особистості з гнучким розумом; розвиненими потребами до подальшого пізнання та самостійних дій; певними навичками та творчими здібностями.
У технології розвивального навчання математики в початкових класах досить дієвим є застосування опорних схем.
Форма подання опорних схем обчислювальних прийомів може бути різна
залежно від етапу роботи над цим прийомом, мети тощо. Вчитель під час
пояснення, наприклад множення двоцифрового числа на одноцифрове, подає на
дошці такий зразок обчислення:
| 18-4 = / \ 10 8 | 10-4-40 8 • 4 = 32 40 + 32 = 72 |
Якщо вчитель на дошці, а учні в зошитах виконуватимуть розгорнутий запис обчислювальних прийомів, то хід міркування учня під час обчислень буде більш усвідомленим.
63 + 28 =60 + 3 + 20 +8= 60 +20 +3 + 8 = 80 + 11 = 91.
Наочна інтерпретація має велике значення для розв'язування задач. Вона набуває вигляду короткого запису, схеми чи малюнка. При цьому кожний вид наочності може мати різні варіанти. Вибір того чи іншого виду наочності зумовлений передусім дидактичною метою роботи над задачами: розв'язати задачу окремими діями з письмовим поясненням чи без нього; скласти вираз із письмовим поясненням чи записати (назвати) відразу вираз;
розв'язати задачу різними способами і встановити, який з них раціональний; розглянути тільки залежність між величинами задачі та ін.
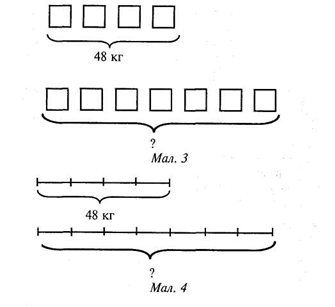
Скорочений запис текстової задачі можна подати по-різному. Таблична форма запису задачі більш абстрактна, ніж схема. Тому під час первинного ознайомлення, наприклад, із задачею: "В чотирьох однакових ящиках 48 кг яблук. Скільки кілограмів яблук у семи таких ящиках?" — доцільно змоделювати її у вигляді схеми (мал. 3) або графічної ілюстрації (мал. 4), які вчитель може виконати на дошці:
Цікавий досвід роботи з використання опорних схем і таблиць на уроках математики має вчителька М. Малько (ЗОШ №12 м. Кіровограда).
Залучити кожного учня до активної діяльності на всіх етапах уроку, сформувати поняття, стійкі навички допомагають опорні схеми. Дуже важливо, щоб вони не висіли, як плакати, а постійно підключалися до роботи на уроці. Краще розташовувати їх у правому верхньому кутку дошки. Коли учень відповідає на запитання вчителя, користуючись опорою, зникає скутість, страх помилитися. Схема стає алгоритмом міркування й доказу, а вся увага спрямовується на суть, міркування, усвідомлення залежностей і зв'язків. З огляду на це вчитель пропонує декілька опорних схем, які використовує на уроках математики.
4 +? = 6
При додаванні:
дивись на останнє число;
пригадай склад цього числа.
8 -? = 5
При відніманні:
дивись на перше число;
пригадай склад цього числа.






