Есептеудің нәтижелері 8.3.1 және 8.3.2 кестелерінде келтірілген.
Магнит өрісі кернеулігінің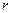 
-ден тәуелділігі (8.3.1-кесте)
| Нвн | ішкі | сым | Нвш | сыртқы | сым | |||||
r×10  ,м
| ||||||||||
| Н, А/м | 29,47 | 58,94 | 88,42 | 88,42 | 66,31 | 53,05 | 44,21 | 37,89 | ||
Магнит индукциясының 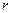-ден тәуелділігі (8.3.2-кесте)
| Ввн сым | ішінде | Ввш сым | сыртында | |||||||
| r×10 , м
| ||||||||||
| В, тл | 3,7×10
| 7,4×10
| 11,1×10
| 11,1×10 
| 8,33×10
| 6,67×10
| 5,56×10
| 4,76×10
| ||
Магнит өрісінің кернеулігі 
және магнит индукциясы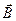 
сымның бетіндегі жанаманың бойымен бағытталған, 
және 
болады, мұндағы 
-кернеудің потенциялдық құрауышы. Осыдан, шекаралық шартқа сәйкес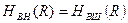 
сымның бетінде болады. Магнит индукциясы үшін 
және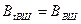 
, және шекаралық шартқа сәйкес 
, осыдан 
сымның бетінде болады.
 |
және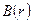 
тәуелділік графиктері 8.3.3 және 8.3.4 суреттерінде келтірілген.
Сурет 8.3.3
Сурет 8.3.4 
Сымның ішіндегі магнит ағынын есептеу.
Ұзындығы 
бөлікте сымның ішіндегі магнит ағыны (сурет 8.3.5) мынаған тең:
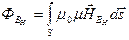(8.3.11)
мұндағы 
-магнит өрісінің кернеулік векторы;
-сымның қимасына ‘бізден’ перпендикулярлы бағытталған.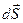 
векторы да сымның қимасына перпендикуляр бағытталған.
 |
Сурет 8.3.5
Ф 
ағынды есептейік:
(8.3.12)
Сымның ішіндегі ағын іліністігін 
есептеу.
Сымның ішіндегі ағын іліністігін мына формула бойынша анықтайық (8);
, (8.3.13)
мұндағы 
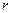- радиуысы 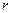-ге тең көлдененгі қимадан өтетін ток.
-ауданы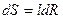 
беттіктен элементарлы магнит ағыны.
Осыдан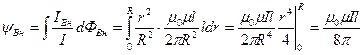 
(8.3.14)
Сымның ішкі индуктивтілігін есептеу. Ұзындығы 
сымның бөлігіндегі индуктивтілікті есептейік. Сымның бөлігіндегі ішкі индуктивтілік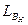 
ағын іліністігімен байланысты теңдеуі;
(8.3.15)
Осыдан 
(8.3.16)
векторлық потенциалын есептеу.
Векторлық потенциал мына формула бойынша анықталады.
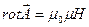(8.3.17)
Түзу сым үшін векторының бағыты ток тығыздығының векторларының бағытымен бағыттас, яғни сымның білігі бойымен бағытталады.
Цилиндрлік координаттар жүйесін қолданамыз: 
. 
білік сымның білігі- мен бағытталсын. векторының тек бір ғана проекциясы болады 
.
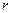векторы білігіне және радиуысына перпендикулярлы бағытталған (
) және оның бір ғана проекциясы болады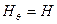 
.
Осыдан векторлық потенциялды есептеуге болатын формуланы шығарамыз: 
(8.3.18).
Сымның ішінде 
(8.3.19)
болған жағдайда 
болсын, осыдан 
+.
Сымның ішіндегі векторлық потенциал мынаған тең:
(8.3.20).
Сымның сыртында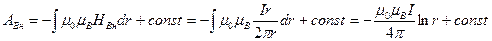 
(8.3.21).
Сымның бетіндегі векторлық потенциал үздіксіз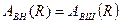 
.
Осыдан 
және 
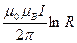+(8.3.22).
Сымның сыртындағы векторлық потенциал мынаған тең:
(8.3.23).
қашықтықта сымның ішіндегі және 
қашықтықта сымның сыртындағы векторлық потенциалды есептейік:
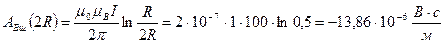
8.3.2. Қосөткізгіштік желінің магнит өрісін есептеу.
Қосөткізгіштік желі ұзын цилиндрлік сымдардан тұрады. Сымдардың радиустары бірдей және 
тең. Сымдар параллель орналсқан, біліктерінің арасындағы ара қашықтық 
. Желінің ішіндегі ток 
. Қоршаған орта-ауа.
 |
Сурет 8.3.6
Қосөткізгіштік желінің магнит өрісінің кернеулігін есептеу.
Қосөткізгіштік желінің магнит өрісінің кернеулігі келесі формула бойынша анықталады:
(8.3.24)
мұндағы -бірінші сымдағы ток бойынша берілген магнит өрісінің кернеулік векторы.
