g 
=g 
=g 
=0,33См.
- Э.Қ.К.-ң қарастырылатын түйінге қосылған барлық тармақтар үшін сәйкес өткізгіштігіне көбейтінділерінің алгебралық қосындысы. Егер Э.Қ.К. қарастырылатын түйінге бағытталса, ‘+’ таңбасы жазылады, егер Э.Қ.К. түйіннен бағытталса ‘-‘ таңба жазылады.
Түйіндік потенциалдарды есептеу теңдеулері келесі түрде жазылады;
(1.6)
Анықтауыштар арқылы 
потенциалдарын есептейміз.
Теңдеулер жүйесі үшін анықтауыштар мынаған тең:
потенциалдарын келесі формулалар бойынша анықтаймыз:
Электр тізбегінің тармақтарындағы тоқтарды Ом заңы бойынша анықтаймыз;
(1.7)
1.5 теңдеулер жүйесін ЭВМ-де шығаруға болады.
Мұндай жағдайда түйіндік потенциалдар теңдеулерін матрицалық түрде жазу қажет.
Матрицалық түрдегі түйіндік потенциалдар теңдеулері:
1.4 Электр тізбек схемасындағы тармақтардың біреуінің тоғын активті қосполюсник тәсілімен анықтау.
I 
тоғын анықтаймыз.
I тоғы бар ерекшеленген тармақ жалғанған электр тізбекті ажыратылған тармақтың қысқыштарындағы U 
кернеуіне тең Е 
Э.Қ.К.бар эквивалент көзімен және берілген тармақ жалғанған R 
кедергісімен ауыстырайық (1.3-сурет).
 |
1.3-сурет
I -тоғын келесі формуламен есептейміз:
(1.8)
Е =U -ті есептейміз. I тоғы бар тармақты ажыратып, U –ті анықтаймыз:
 |
1.4-cурет
U =-R I 
+E -E 
+R I 
. (1.9)
I және I контурлық тоқтар тәсілімен анықталады:
(1.10)
R кедергісін анықтайық. Е , Е , Е 
, Е 
Э.Қ.К.-н нөлге тең деп аламыз (1.5-сурет).
Сурет 1.5 Сурет 1.6
R , R 
, R 
кедергілерінің үшбұрышын оған эквивалент жұлдызшаға түрлендіреміз (1.6-сурет):
I тоғы мынаған тең болады:
1.5 Қуаттар балансының теңдеуін құру.
Электр тізбегіндегі барлық Э.Қ.К. көздерінің және тоқ көздерінің Р 
қосындылық қуаты, Р 
кедергілерде шығындалған қосындылық қуатына тең болады:
Р = Р
E 
I – контурлық тармақтың Э.Қ.К. көзінің қуаты; Егер Е Э.Қ.К.-ң және I тоғының оң бағыттары сәйкес болса, қуат оң болады, егер Е Э.Қ.К.-ң және I тоғының оң бағыттары қарама-қарсы болса, қуат теріс болады;
U 
J – тоқ көзінің қуаты. U – тоқ көзінің қысқыштарындағы кернеу. Егер U – ң және I – ң оң бағыттары сәйкес келсе, қуат оң болады, егер U мен I – ң оң бағыттары қарама-қарсы болса, қуат теріс болады;
- контурлық тармақтағы кедергідегі қуат.
Барлық Э.Қ.К. көздерінің және тоқ көзінің қосындылық қуаты:
U 
– ті анықтаймыз:
Кедергілердегі қосындылық қуат:
(1.16)
Есептеулердің қателігін анықтаймыз:
(1.17)
1.6 Электр тізбек схемасының сыртқы контуры үшін потенциалдық диаграммасын тұрғызу.
Электр тізбегінің кез-келген түйінінің потенциалын 0-ге тең деп аламыз, j =0 болсын, сонда:
 |
(1.18)
1.7-сурет
2.Бір фазалық синусоидалық тоқтың электр тізбектерін есептеу.
Бір фазалық синусоидалық тоқтың тармақталған тізбектеріндегі есептеуді 2.1- суретте көрсетілген схема мысалында қарастырайық.
 |
2.1-сурет
Есептеулер үшін бастапқы берілгендері: 
Синусоидалық тоқты тізбектерді есептеумен байланысты негізгі сұрақтарды қарастырайық.
2.1 Дифференциалдық және символикалық жазбалар түрлерін қолданып, Кирхгоф заңдарының негізінде схеманың барлық тармақтарындағы тоқтарды есептеу үшін теңдеулер құру.
Тармақтардағы тоқтардың бағытын кез-келген бағытпен аламыз (2.1-сурет). Дифференциалдық түрде, яғни тоқтар мен кернеулердің лездік мәндері үшін теңдеулер құрайық. Кирхгофтың бірінші заңы бойынша түйінге сәйкес тармақтардағы лездік тоқтардың алгебралық қосындысы нөлге тең. Схемада екі түйін, сол себептен Кирхгофтың бірінші заңы бойынша бір теңдеу құраймыз. Кирхговтың екінші заңы бойынша схеманың тұйықталған контурындағы барлық кернеу көздерінің лездік Э.Қ.К.-ң алгебралық қосындысы сол контурдың барлық қалған элементтерінің лездік кернеулерінің алгебралық қосындысына тең. Схемада екі тәуелсіз контур, сол себептен Кирхгофтың екінші заңы бойынша екі теңдеу құраймыз. Сонымен, Кирхгофтың заңдары бойынша құралған дифференциалдық түрдегі теңдеулер жүйесін аламыз.
(2.1)
Теңдеулерді символикалық түрде жазу үшін тоқтардың, Э.Қ.К.-дің, кернеулердің лездік мәндерін комплекс бейнелерімен алмастыру қажет.
Сонда, Кирхгофтың заңдары бойынша жазылған символикалық түрдегі теңдеулер жүйесін аламыз:
(2.2)
Алынған теңдеулер жүйесінің шешімі тармақтардағы тоқтардың комплекстік әсер етуші мәндерін анықтауға мүмкіндік береді. Бұл есепті контурлық тоқтар және түйіндік потенциалдар тәсілдерін пайдаланып тиімдірек шығаруға болады.
2.2 Контурлық тоқтар тәсілімен комплекстік тоқтарды есептеу
 |
i
және i 
контурлық тоқтардың бағытын сағат тілімен бағыттайық және осы тоқтар үшін Кирхгофтың екінші заңы бойынша теңдеулер құрайық (2.2-сурет).
2.2-сурет
Z , Z , Z арқылы сәйкес тармақтардың комплекстік кедергілері белгіленген. Z =R +jX 
; Z =R ; Z =j (Х 
-X 
). Ė мен Ė комплекстік әсер ететін Э.Қ.К.-ң мәндерін көрсетеді.
Ė =20e 
,B; Ė =40e 
,B.
Кедергілер мен ЭҚК-тің сан мәндерін қойып, келесі теңдеулер жүйесін аламыз;
(2.4)
Матрицалық түрдегі (2.4) теңдеулер:
(2.5)
(2.5) - жүйесін Крамер әдісімен шығарамыз.
2.1-суретте алынған тоқтардың бағыты бойынша табылған контурлық тоқтардың комплекстері арқылы тармақтардағы тоқтардың комплекстерін анықтаймыз:
2.3 Түйіндік потенциалдар тәсілімен тоқтардың комплекстерін есептеу.
(2.2-сурет) схемада екі түйін сол себептен ТПТ-ң жеке бір жағдайы болатын екі түйіндер тәсілін қолданған жөн.
Түйіндер арасындағы кернеу комплексін есептейміз:
, (2.6)
мұндағы, 
Тармақтардағы тоқтар комплекстерін Ом заңы бойынша есептейміз:
2.4 Қуаттар балансы
Комплекстік қуаттар балансының теңдеуі.
(2.7)
Э.Қ.К. көзінің комплекстік қуаты:
, (2.8)
Мұндағы 
–комплексі, İ тоғымен байланысты.
, (2.9)
Көздердің комплекстік қуаттарын анықтайық.
Пайдаланушылардың комплекстік қуаттары:
Есептеудің қателігі:
2.5 Тоқтардың векторлық диаграммасы мен біріктірілген топографиялық диаграмма.
Топографиялық диаграмма тұрғызу үшін тізбектегі нүктелердің комплекстік потенциалдарын есептеп, содан кейін алынған мәндерді комплекстік жазыққа түсіру қажет. Екі нүктесінің потенциалын 0-ге тең деп аламыз, j =0 және тізбектегі қалған барлық нүктелердің комплекстік потенциалдарын көрсетейік.
 |
2.3-сурет
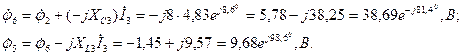
Потенциалы нөлге тең деп алған 2 нүктесін координата басына орналастырамыз, осыдан кейін тізбектегі қалған нүктелерін белгілейтін векторлар тұрғызамыз. Мысалы, 3 нүктесінің потенциалы j =20,887e 
, В. Координатаның басынан нақты сандар оң жарты осімен салыстырғанда –107,6 
бұрышпен түзудің кесіндісін жүргіземіз, және осы кесіндіге белгілеп алынған масштабпен 3 нүктесінің потенциалын яғни 20,87 В. шамасын орналастырамыз. Осылай 3 нүктесінің топографиалық диаграммадағы орналасқан жерін табамыз. Тізбектегі қалған нүктелердің орнын берілген жолмен тауып, 2.3 суреттегі схемадағы орналасуына сәйкес қылып, нүктелерді түзу кесінділермен қосамыз. Іс жүзінде алынған топографиялық диаграмма 2.4 суретінде көрсетілген. Суретте тоқтардың векторлық диаграммасы да тұрғызылған.
 |
2.4-сурет
2.6 Индуктивтік байланысқа комплекстік түрде Кирхгоф теңдеуін
құру.
Бірінші және үшінші индуктивтік орауышта, индуктивтік байланысқа қатысты өзара М 
индуктивтігі көрсетілген.Схемада нүктелер орауыштың аттас қысқышын қарастырамыз 
Индуктивтік байланысқа Кирхгоф заңдары бойынша кешенді турде теңдеулер құру. Кирхгофтың екінші заңымен теңдеулер құрған кезде өздік индуктивтік құрған кернеуді к‰штерді орам қысқышында пайда
болатын кернеу есебінде алуға болады.Комплекстік түрде көрсетілген өзара индукцияны кернеуі кедергімен өздік индукцияның кешенді тоғының Z 
= 
wM=j 
бойынша қатысады Сонымен бірінші орамдағы 
jI үшінші орамдағы 
jX 
I ,өздік индукцияның кернеуінің бағыты тізбек бағытымен салыстыра отырып және келесі орамдағы тізбек бағытымен салыстыра анықталады.Егерде осы бағыттар аттас қысқыштармен бірдей
болса,онда кернеу “+”оң таңбамен алынады.Керісінше,”-“теріс таңбамен алынады.Көрсетілген схемаға теңдеулер құруды көрсетейік.(2.5-сурет).
 |
2.5-сурет
Тұйықталған тізбектің жүру бағыты сағат тілімен бағыттас
İ1+İ2-İ3=0;
Z1İ1-Z2İ2-ZM13İ3=-Ė2;
Z2İ2+Z3İ3-ZM13İ1=Ė2+Ė3.
Бірінші орамдағы Z İ өздік индукция кернуі “-“ таңбамен алынады, себебі тізбектегі жүру бағыты 1-ші орамның аттас қысқышына шығып тұр, ал ток İ ‰шінші орамның аттас қысқышына кіріп тұр. Осылай 3-ші орауышқа арналған контурдаѓы кернеу және бірінші орауыштағы ток бағыты осы орауыштардың аттас қысқыштарына қатысты “-“таңбамен жазылады.
3.Үш фазалы тізбектің статикалыќ жүктемесін есептеу.
3.1-суретте берілген үш фазалы симметриялы тізбекті қарастырамыз
3.1-сурет
Үш фазалы генератордың фазалық ЭҚК-і: Eф=127B.
Жүктеме кедергісі R1=86Ом, R =68Ом, XL1=38Oм, XL2=23Oм, XC1=38Oм, Cс =77 Oм.
