Тәуелсіз бастапқы шарттар:


6.1.2. Диференциялдық теңдеулер жүйесін құру. Теңдеулер коммутациядан кейінгі электр тізбегі үшін Кирхгоф заңдары бойынша құрылады ( ):
):

 (6.4.а)
(6.4.а)
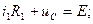 (6.4.б)
(6.4.б)
 (6.4.в)
(6.4.в)
 (6.5)
(6.5)
 (6.6)
(6.6)
 өтпелі кернеуін тізбектің ерікті және еріксіз режимдерінің қосындысы түрінде ұсынайық,
өтпелі кернеуін тізбектің ерікті және еріксіз режимдерінің қосындысы түрінде ұсынайық,
 (6.7)
(6.7)
6.1.3. Коммутациядан кейінгі тізбектегі еріксіз режимдегі  индуктивтік кернеуді анықтау.
индуктивтік кернеуді анықтау.
Тізбектегі коммутациядан кейінгі еріксіз режимдегі  индуктивтік тоқ тұрақты, сондықтан
индуктивтік тоқ тұрақты, сондықтан
 (6.8)
(6.8)
6.1.4. Ерікті режимдегі 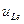 индуктивтік кернеуін анықтау.
индуктивтік кернеуін анықтау.
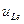 -ні табу үшін коммутациядан кейінгі тізбектің сипаттаушы теңдеуін алу керек. Сипаттаушы теңдеу құрудың ең оңай әдісі - кіру кедергі әдісі.
-ні табу үшін коммутациядан кейінгі тізбектің сипаттаушы теңдеуін алу керек. Сипаттаушы теңдеу құрудың ең оңай әдісі - кіру кедергі әдісі.
Коммутациядан кейінгі тізбектің кіру кедергісін  комплекс түрде жазайық. Кіру кедергісін тізбектің тоқ көзі бар тармағынан басқа кез-келген тармағына қатысты қарастыруға болады. ЭҚК көзі бар тармаққа қатысты тізбектің
комплекс түрде жазайық. Кіру кедергісін тізбектің тоқ көзі бар тармағынан басқа кез-келген тармағына қатысты қарастыруға болады. ЭҚК көзі бар тармаққа қатысты тізбектің  кіру кедергісінің комплекс түрі мына түрде жазылады:
кіру кедергісінің комплекс түрі мына түрде жазылады:
 =
=  (6.9)
(6.9)
 формуласындағы
формуласындағы  орнына Р жазамыз және алынған Z(P) теңдеуін нөлге теңестіреміз:Z(P)=0
орнына Р жазамыз және алынған Z(P) теңдеуін нөлге теңестіреміз:Z(P)=0

 (6.10)
(6.10)
(6.10) теңдеуінің алымын нөлге теңестіреміз
 (6.11)
(6.11)
(6.11) теңдеуі тізбектің сипаттаушы теңдеуі болып табылады.
(6.11) сипаттаушы теңдеуіне берілген  мәндерін қоямыз:
мәндерін қоямыз:
 (6.12)
(6.12)
(6.12) сипаттаушы теңдеуінің түбірлерін есептейміз

Табылған түбірлер комплекс-түйінді, яғни 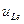 индуктивтік кернеуінің еркін құраушысын келесі түрде іздейміз:
индуктивтік кернеуінің еркін құраушысын келесі түрде іздейміз:
 (6.13)
(6.13)
мұндағы А мен Ψ интегралдау тұрақтылары.
6.1.5. Интегралдау тұрақтыларын анықтау.
uL өтпелі индуктивтік кернеуін келесі түрде жазамыз:
 (6.14).
(6.14).
А, Ψ интегралдау тұрақтыларын табайық. Оларды uL(0) кернеудің бастапқы мәндері және оның бірінші ретті туындысы u'L (0) бойынша табады.
u'L(t)-ны табайық:


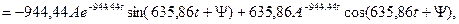 (6.15)
(6.15)
 uL(0) және u'L (0) теңдеулерін уақыт t=0 үшін жазамыз
uL(0) және u'L (0) теңдеулерін уақыт t=0 үшін жазамыз
 (6.16)
(6.16)
uL(0) және u'L(0) мәндерін коммутациядан кейінгі тізбек үшін Кирхгоф заңдары бойынша t=0 үшін құрылған теңдеулерді (6.4а-6.4в) шешу арқылы және сол теңдеулерге і3(0)=2.5 A, uc(0)=120 B тәуелсіз бастапқы шарттарды қою арқылы табамыз

 (6.17.а)
(6.17.а)
 (6.17.б)
(6.17.б)
 (6.17.в)
(6.17.в)
(6.17в) теңдеуіне uL(0)-ді табамыз:
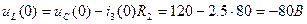
u'L(t)-ні (6.4в) теңдеуін дифференциалдау арқылы табамыз:
 (6.18)
(6.18)
мұндағы 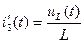 (6.19)
(6.19)
 (6.20)
(6.20)
(6.19) бен (6.20)-ны (6.18)-ге қойып u'L(t)-ні табамыз:
 (6.21)
(6.21)
t=0 уақыт моменті үшін u'L(t)-ні жазамыз:
 (6.22).
(6.22).
(6.17а) және (6.17б) теңдеулерін пайдаланып і2(0) тогын есептейік

Табылған uL(0) және u'L(0) мәндерін (6.16) теңдеуіне қоямыз:
 |
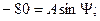 (6.23а)
(6.23а)
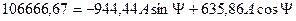 (6.23б)
(6.23б)
(6.23.а)-дан
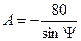 (6.24)
(6.24)
тауып, (6.23.б)-ға қоямыз.
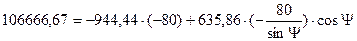 (6.25)
(6.25)
(6.25) теңдеуінен tgΨ-ді табамыз:
tgΨ= -1,635
яғни: Ψ=arctg(-1,635)=-58,5º
(6.24) теңдеуінен А-ны табамыз: А=93,8.
Табылған А мен Ψ мәндерін (6.14) теңдеуіне қоямыз, сөйтіп uL ауыспалы кернеуін табамыз
uL =93,8e-944,44tsin(635,86t-58,5º) B,
6.2. Өтпелі процесстерді есептеудің операторлық тәсілі.
6.2.1. Эквиваленттік операторлық схема.
Тәуелсіз бастапқы шарттар: і3(0)=2,5 A, uc(0)=120 B.
 |
Есептің бастапқы шарттары нөлдік емес. Эквиваленттік операторлық схема Li3(0) және
 ЭҚК-ін қамтиды, және қосымша ішкі ЭҚК оң бағыттары осы тармақтың тоғының оң бағытымен сәйкес етіп алынған. Эквиваленттік операторлық схема 6.3- суретінде көрсетілген.
ЭҚК-ін қамтиды, және қосымша ішкі ЭҚК оң бағыттары осы тармақтың тоғының оң бағытымен сәйкес етіп алынған. Эквиваленттік операторлық схема 6.3- суретінде көрсетілген.
6.3 – сурет
6.22. Индуктивтік кернеу мен тоқ бейнесін анықтау.
UL(Р) операторлық кернеуді келесі формуламен табамыз:
UL(Р)= I3(P) PL - Lі3(0) (6.26).
I3(P) тоғын операторлық түрдегі Кирхгоф заңдарын, контурлық тоқтар тәсілін, түйіндік потенциалдар тәсілін немесе эквивалент генератор тәсілін пайдаланып табуға болады.
I3(P) тоғын контурлық тоқтар тәсілімен табайық. I11(P)= I1(P) және I22(P)= I3(P) болғандықтан, контурлық теңдеулер келесі түрде жазылады:
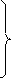
 (6.27).
(6.27).
Осы теңдеулерді шешіп I3(P) тоқты табамыз:

мұндағы

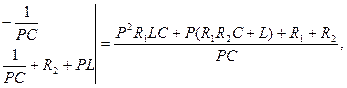


Яғни  (6.28).
(6.28).
Табылған  тоғын (6.26) теңдеуіне қойып, операторлық индуктивтік кернеуді табамыз
тоғын (6.26) теңдеуіне қойып, операторлық индуктивтік кернеуді табамыз
 (6.29).
(6.29).
Мұндағы



6.2.3 Индуктивтік кернеуді анықтау.
UL кернеуін жіктеу теоремасы бойынша табамыз.
F2(Р)=0 сипаттаушы теңдеуінің түбірлері:
 ;
;
Жіктеу теоремасын қолданып, келесі формуламен ULтүпнұсқасын табамыз:
 (6.30).
(6.30).
F'2(Р) табамыз:




6.2.4.  индуктивтік кернеуінің уақыт бойынша өзгеру графигін салу.
индуктивтік кернеуінің уақыт бойынша өзгеру графигін салу.
Графикті табылған аналитикалық шешімге сүйене отырып  және
және  интервалында саламыз
интервалында саламыз 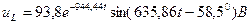
Мұндағы α = 944,44 c-1 - өшу коэффициенті.
Ал 

 (t) графигін салу үшін уақыттың әр түрлі моменттеріндегі
(t) графигін салу үшін уақыттың әр түрлі моменттеріндегі  кернеуінің мәндерін есептейік.
кернеуінің мәндерін есептейік.
6.1 кестесінде есептеулердің нәтижелері келтірілген.
6.1-кесте. UL кернеуінің уақытқа тәуелділігі.
| 0,5 | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 | |
  
| -80 | -37,8 | -13,7 | -1,5 | 3,5 | 4,8 | 4,8 | 3,2 |
Ескерту. sin(635,86t-58,5º) теңдеуін есептегенде φ=58,5º бұрышын радианға келтіру керек.
 |
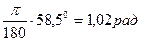
Кернеу графигі 6.4 суретінде көрсетілген
6.4 сурет.
7. Параметрлері таратылған тізбектерді есептеу.
Мысал ретінде электр энергиясының үш фазалы тасымалдау желісін есептеп көрейік. Ұзындығы l=1200 км желі UH =110 кВ номиналдық фазалық кернеу және f=50 Гц жиілікпен жұмыс істейді. Желінің бастапқы параметрлeрі:  ,
,  . Желінің бір фазасының активтік қуаты P2=20 MBт болатын жүктемені қамтиды, жүктемедегі U2 кернеу Uн номиналдық кернеуге тең, жүктеменің қуат коэффициенті cos φ2=0,86.
. Желінің бір фазасының активтік қуаты P2=20 MBт болатын жүктемені қамтиды, жүктемедегі U2 кернеу Uн номиналдық кернеуге тең, жүктеменің қуат коэффициенті cos φ2=0,86.
.
7.1. Желінің екінші ретті параметрлерін анықтау.
Комплекс кедергілермен 1км желіге өткізгіштікті табамыз:
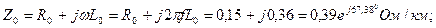 (7.1.)
(7.1.)
 (7.2.)
(7.2.)
Желінің екінші ретті параметрлерін есептейміз:
 |
Толқындық кедергі
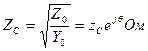 ;
;
Таралу коэффициенті 
 (7.3.)
(7.3.)
 (7.4.)
(7.4.)
мұндағы 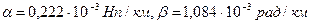
7.2. Желінің басындағы тоқ пен кернеуді, желінің аяғындағы тоқты және желінің ПӘК-ін есептеу.
Жүктеменің бір фазасындағы активті қуат
P2=U2I2cosφ2, (7.5.)
Мұндағы U2=UH=110кВ, P2=1000 MBт, cos j2=0,86.
Осы жерден желінің аяғындағы әсер етуші тоқты табамыз
 (7.6.)
(7.6.)
Желінің аяғындағы тоқтың бастапқы фазасын анықтаймыз:
 , егер
, егер  болса, онда
болса, онда

Желінің аяғындағы комплекс тоқ

Желінің басындағы  кернеуді және
кернеуді және  тоқты гиперболалық функциясы бар желінің теңдеуі арқылы табамыз:
тоқты гиперболалық функциясы бар желінің теңдеуі арқылы табамыз:
 (7.7)
(7.7)
 (7.8)
(7.8)
chγl, shγl гиперболалық функцияларының мәндерін келесі формулалар арқылы табуға болады:

Tабылған chγl, shγl мәндерін (7.7), (7.8) теңдеулеріне қойып  ,
,  -ді анықтаймыз..
-ді анықтаймыз..  Желінің басындағы активті қуат:
Желінің басындағы активті қуат:
 (7.9)
(7.9)
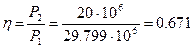 (7.10)
(7.10)
7.3. Желінің аяғындағы жүктемені алып тастағандағы желінің аяғындағы  кернеуді және желінің басындағы тоқты анықтау.
кернеуді және желінің басындағы тоқты анықтау.
Желінің басындағы кернеу номиналдық кернеуге тең 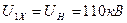
Желінің соңындағы кернеу
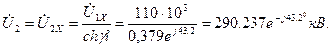 (7.11)
(7.11)
Желінің басындағы тоқ
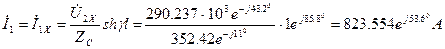 (7.12)
(7.12)
7.4. Келісілген жүктеме режимін есептеу
Келісілген жүктеме режимі:


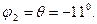
Жүктеме кернеуі (желінің соңы) 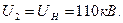
Желінің аяғындағы тоқ
 (7.13)
(7.13)
Жүктемеге берілетін нақты қуат
 (7.14)
(7.14)
Желінің басындағы кернеу
 (7.15)
(7.15)
Келісілген жүктеме режимінде желінің кіру кедергісі толқындық кедергіге тең болады 
Желінің басындағы тоқ
 (7.16)
(7.16)
Желіге берілетін қуат
 (7.17)
(7.17)
Желінің ПӘК-і
 (7.18)
(7.18)
8. Электр және магнит өрістерін есептеу
8.1. Электростатикалық өрістерді есептеу
8.1.1. Екі диэлектриктің бөліну шекарасының маңындағы электр зарядтарының өрісі
Диэлектрлік өтімділігі ε1=6 және ε2=4 болатын екі ортаның бөлінуінің жазық шекарасына параллель және өзара параллель екі көлденең қималарының радиусы R=6·10-3м бірдей ұзын сымдар жүргізілген. Олардың өзара арақашықтығы d=0,8 м, ал олардан шекаралық жазықтыққа дейінгі арақашықтықтар h1=0,5 м және h2=0,65 м. Олардың зарядтары τ1=-1,5·10-9 Кл/м және τ2=1·10-9 Кл/м. Екі ортаның бөліну жазықтығымен сымдардың өзара орналасуы
8.1.1-суретінде көрсетілген.

8.1.1-сурет
Электр зарядтары әртүрлі қасиеттері бар екі ортаның бөліну шекарасының маңында болғанда біртекті емес орталардағы электростатикалық өрістерді есептегенде бейнелер тәсілі қолданылады.
Бейнелер тәсілінің мәнісі келесіде, біртекті емес ортаның орнына біртекті орта қарастырылады, ал біртекті еместіктің әсері жалған заряд еңгізу арқылы есептеледі.
Сымдар арасындағы кернеуді анықтау
Сымдар арасындағы кернеуді келесі формуламен анықтаймыз:
 (8.1.1)
(8.1.1)
мұндағы φ1-заряды τ1 сымның бетіндегі потенциал;
φ2-заряды τ2 сымның бетіндегі потенциал.
Сымдардың φ1 және φ2 потенциалдары берілген τ1, τ2 және жалған зарядтар тудыратын потенциалдардың алгебралық қосындысына тең:

 (8.1.2)
(8.1.2)
Бұл жерде диэлектрлік өтімділігі  біртекті орта қарастырылады (8.1.2- сурет).
біртекті орта қарастырылады (8.1.2- сурет).
 болғандықтан,
болғандықтан, 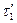 пен
пен  ,
, 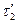 пен
пен  таңбалары бойынша қарама-қарсы.
таңбалары бойынша қарама-қарсы.


Сымдар арасындағы U кернеуді келесі формуламен есептейміз:
 |
 мұндағы
мұндағы 
8.1.2-сурет
Шекаралық жазықтықтағы К нүктесінде σбайл байланған зарядтардың тығыздығын анықтау
Байланған зарядтар тығыздығы мынаған тең:
σбайл= -(P1n-P2n), (8.1.3)
мұндағы P1n,P2n- диэлектрлік өтімділігі ε1 ортадағы және диэлектлік өтімділігі ε2 ортасындағы поляризация векторларының нормальды құраушылары.
 (8.1.4)
(8.1.4)
Осы жерден
 (8.1.5)
(8.1.5)
мұндағы D1n-D2n=0, өйткені шекаралық жазықтықтағы бос заряд тығыздығы 0-ге тең;
Е1n, Е2n –диэлектрлік өтімділіктері ε1 және ε2 орталарындағы шекаралық жазықтықтағы электр өрісінің кернеулік векторларының нормальды құраушылары.
E1n кернеулігі берілген τ1 және τ2 зарядтары арқылы және τ1´ және τ2´ жалған зарядтары арқылы есептеледі.
 |
(8.1.3-сурет).
 кернеуліктері келесі формуламен есептеледі:
кернеуліктері келесі формуламен есептеледі:
 (8.1.6)
(8.1.6)
 (8.1.7)
(8.1.7)
 (8.1.8)
(8.1.8)
 (8.1.9)
(8.1.9)
мұндағы

К нүктесінің координаттары: XK=0.25 м, YK=0.
 нормальды құраушылары мынаған тең:
нормальды құраушылары мынаған тең:
 (8.1.10)
(8.1.10)
8.1.3 суретінде  векторларын салғанда τ1, τ2, τ1´, τ2´ зарядтарының таңбалары ескерілген.
векторларын салғанда τ1, τ2, τ1´, τ2´ зарядтарының таңбалары ескерілген.






