және 
кернеуліктері модуль бойынша мынаған тең:
(8.3.25)
(8.3.26)
, 
векторларының 
және 
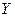біліктеріне проекциялары мынаған тең:
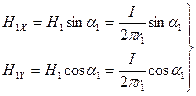
(8.3.27)
, (8.3.28)
мұндағы 
, 
, 
.
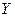векторының және біліктеріне проекциясы келесі формула бойынша есептеледі: 
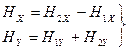(8.3.29)
Осыдан 
(8.3.30)
Координаттары 
, 
нүктесінде 
-ты есептейік.
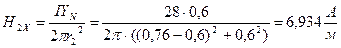
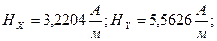
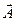векторлық потенциалын есептеу.
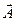нүктесіндегі векторлық потенциалы келесі формуламен анықталады:
(8.3.31)
және 
векторлық потенциалдары сымдардың біліктеріне параллель бағытталған, яғни токтардың бағытымен бағыттас.
 |
Сурет 8.3.7
Сымның сыртындағы 
және 
векторлық потенциалдары келесі формулалар бойынша анықталады:
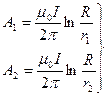(8.3.32).
Осыдан 
(8.3.33).
Координаттары , нүктесі үшін
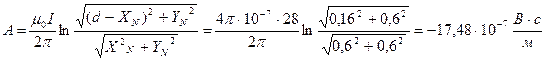
Қосөткізгіштік желінің сыртқы индуктивтілігін есептеу.
 |
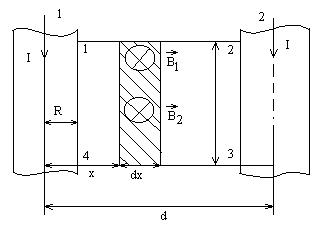Сурет 8.3.8
Ұзындығы 
бөліктегі желімен ілініскен сыртқы магнит ағыны келесі формуламен есептеледі:
(8.3.34).
Магнит индукциясы 
келесі формуламен анықталады:
(8.3.35).
мұндағы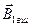 
- бірінші оңаша сымның магнит индукциясы;
- екінші оңаша сымның магнит индукциясы;
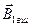, - магнит индукциялар сымдардың біліктерінен өтетін жазықтыққа перпендикулярлы бағытталған.
Осыдан 
(8.3.36).
Егер контурдан өтетін бағытты 1234 жолымен алсақ, онда және 
бағыттас.
Сыртқы ағын мынаған тең болады:
(8.3.37).
Сыртқы ағын іліністігі 
, өйткені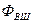 
магнит ағыны 
токпен бір рет ілініскен.
Осыдан 
Желінің бірлік ұзындығына 
сыртқы индуктивтілік
.
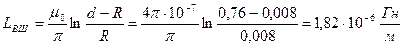8.3.3 Тікбұрышты рамканың жанында орналасқан түзу ұзын сымның магнит өрісін есептеу.
Тұрақты тогы 
тең түзу ұзын сымнан 
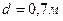қашықтықта жіңішке сымнан жасалған орам саны 
бар тікбұрышты рамка орналасқан. Рамканың бойымен 
ток өтеді. Рамканың екі ені сымның білігіне параллель. Рамканың ендері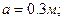 
Сурет 8.3.9
Өзара индукцияның магнит ағынын анықтау.
Тогы рамкадан өтетін магнит өрісінің өзара индукциясының магнит ағынын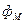 
есептейік.
тогы бар магнит өрісінің магнит индукциясы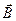 
мына формуламен анықталады:
, (8.3.38).
мұндағ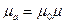ы 
, 
-магнит тұрақтысы;
-ортаға қатысты магнит өтімділігі.
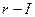тогы бар сымның білігінен элементар ауданға 
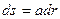дейінгі қашықтық.
Магнит индукциясы 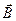“бізге” рамканың көлденең қимасына перпендикулярлы бағытталған.
тогы бар магнит өрісінің өзара индукциясының магнит ағыны 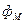келесі формуламен анықталады:
(8.3.39).
Өзара индуктивтілікті анықтау.
рамкасы мен сымның арасындағы өзара индуктивтілікті есептейік. Өзара индуктивтілік келесі формуламен анықталады:
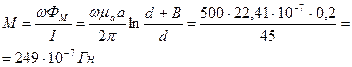(8.3.40).
Рамкаға әсер ететін күшті анықтау.
Рамкаға әсер ететін 
күшті келесі формуламен анықтауға болады:
(8.3.41).
мұндағы 
-магнит өрісінің энергиясы.
, (8.3.42).
мұндағы 
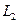-рамканың және сымның индуктивтілігі.
МI 
қосылғышы (8.3.42) формуласында “-” таңбасымен жазылады, өйткені 
тоғы бар магнит өрісінің магнит индукциясы 
рамканың ішінде “бізден” бағытталған. Рамкамен ілініскен өздік индукциясының және өзара индукциясының магнит ағындары бір бірінен алынады.
күші рамкаға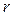 
радиалды бағытта әсер етеді. күшінің әсерімен рамка осы бағытта орнын алмастырады(сымға тартылады),осының нәтижесінде рамка мен сымның арасындағы қашықтық 
өзгереді, сонымен қатар де өзгереді. 
және 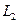тұрақты болып қалады, өйткені рамка қатты және оның өлшемі мен түрі өзгермейді деп есептейміз.
Осыдан күші мынаған тең:
(8.3.43).
Әдебиеттер тізімі
1.Зевеке Г.В,Ионкин П.А., Нетушил А.В, Страхов С.В. Основы теории цепей.-М.:Энергоатомиздат, 1989.-528с.
2.Бессонов Л.А. Теоретические основы электротехники.-М.:Гардарика,1999-536с
3.Нейман Л.Р., Демирчян К.С Теоретические основы электротехники.Т.1.-Л.:Энергоиздат,Ленинградское отделение, 1981.-536с.
4.Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники.Т.2.Л:-Энергоиздат,Ленинградское отделение,1981.-416с.
5.Теоретические основы электротехники. Т.1. Основы теорий линейных цепей /Под.ред. П.А.Ионкина-М.:Высшая школа,1976.-544с.
6.Шебес М.Р., Каблукова М.В. Задачник по теории линейных электрических цепей.-М.:Высшая школа,1990.-544с.
7.Бессонов Л.А Теоретические основы электротехники.Электромагнитное поле.-М. Высшая школа,1986.-263c.
8.Атабеков Г.И.,Купалян С.Д. Тимофеев А.Б. Хухриков С.С. Теоретические основы электротехники.ч2. Нелинейные элекрические цепи;ч.3. Электромагнитное поле.-М. Энергия,1979.-423с.
9.Сборник задач по теоретическим основам электротехники Л.Д.Бессонов,И.Г.Демидова,М.Е.Заруди и др.-М. Высшая школа,1988.-432с.
10.Сборник задач и упражнений по теоретическим основам электротехники /Под ред. П.А. Ионкина. –М.:Энергоиздат, 1982-768с.
Мазмұны
Кіріспе 3
1 Тұрақты тоқтың электр тізбегін есептеу 4
2 Бір фазалық синусоидалық тоқтың электр тізбегін есептеу
тізбектің статистикалық жүктемесін есептеу 16
3 Үш фазалы тізбектің статистикалық жүктемесін есептеу 25
4 Симметриялы емес ережедегі үш фазалы тізбекті симметриялы құрастырылушылар әдіспен есептеу 29
5 Үш фазалы тізбектің синусоидалы емес кернеу мен тогын
есептеу 37
6 Сызықтық электр тізбектеріндегі өтпелі процестер 46
7Параметрлері таратылған тізбектерді есептеу 53
8 Электр және магнит өрістерін есептеу 55
8.1 Электростатикалық өрістерді есептеу 55
8.2 Өткізгіштік ортада электр өрісін есептеу 64
8.3 Тұрақты тоқтың магнит өрісін есептеу 68
Әдебиеттер тізімі 80
