Параллельді жалғанған буындардың эквивалентті беріліс функциясы осы буындардың беріліс функцияларының қосындысына тең (мұнда сигнал жолындағы сумматор кірісінің таңбасы есепке алынады).
Байланыс
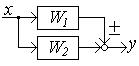
| Түрленуі
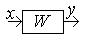
| Беріліс функциясы W=W2 ± W1 | Жалпы түрде
|
3 Кері байланыспен жалғануы (қарсы-параллельді)
Кері байланыспен жалғану кезіндегі эквивалентті беріліс функциясы бөлшекке тең – алымында кірісінен шығысына қарай тура жолдағы буынның БФ жазылған, ал бөлімінде – бір минус кері байланысының тұйықталған контуры (КБТК) бойынша буындарының БФ туындысы жазылған.
Байланыс
| Түрленуі
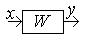
| Беріліс функциясы
|
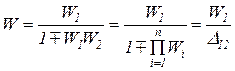
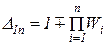- КБТК анықтауышы.
4 Айқасқан байланысты жүйелердегі әсерлердің тасымалдануы – жүйе, аралас түрлі байланыстан тұрған кезінде (таза тізбектей емес, және де таза параллельді емес) қолданылатын құрылымдық түрлендіру ережесі
Қорытынды жүйе өзгермеу үшін тасымалданушы әсердің тізбегіне, буындарды тасымалдау кезінде жоғалған беріліс функциясына, немесе буындардың тасымалдануы кезінде пайда болған кері беріліс функциясына тең келетін, БФ бар жалған (фиктивті) буынды енгізеді.
Ереженің мәнісі мынада: бастапқы сұлбасымен салыстырғанда түрлендіруден кейін пайда болатын кез - келген өзгерулер қорытынды беріліс функциясына әсер етпеуі керек.
Мейсонның ережесі
Ереже жүйені хабарланған граф ретінде қарастырады және оны жеке фрагменттері бойынша түрлендірусіз толығымен сипаттауға мүмкіндік береді.
Бірнеше контурлы жүйенің беріліс функциясы бөлшекті құрайды, алымы тура жолдағы БФ ның туындыларының, бұл жолдарға қатысы жоқ КБТК бірлескен анықтауыштарымен қосындысына тең, ал бөлімі бір минус КБТК мен түйіспейтін анықтауыштар туындысымен жалпы КБТК ның беріліс функцияларының қосындысына тең бөлшекті құрайды.
КБТК анықтауышы, контур бойынша буындардың БФ туындысымен бірліктің айырмасына тең, мысалы, Δ12=1-(- W1W2)=1+ W1W2.
Көрсетілген жүйеніңберіліс функциясының Wzx алымының полиномын құру кезінде х кірісінен z шығысына қарай тура жолдағы БФ (сумматордың беріліс коэффициентіне тең, к=1) есептейміз және барлық кері байланыстың тұйықталған контурларының (КБТК) осы тура жолға қатысты екенін тексереміз, яғни х кірісімен z шығысының арасында орналасуы қажет. Келтірілген мысалда, бұл шарт орындалмайды, сондықтан тура жолдың БФ-сын онымен айқаспайтын КБТК-ның анықтауышына Δ23=1- W2W3 көбейтеміз. Беріліс функциясының бөлімінің полиномын құру кезінде кері байланыстың барлық тұйықталған контурлары бір - бірімен айқасатынын (түйіндескен ортақ нүктесі бар) көреміз, сондықтан барлық контурларға бір саны ортақ болып келеді. Ендеше бөлімінде бір санын жазамыз және плюс-минус таңбасын қойып, әрбір КБТК бойынша буындардың БФ туындысын (әр КБТК бойынша анықтауыштар қосындысы) жазамыз. Соңында:
Жүйе орнықтылығы – бұл жүйені тепе-теңдік күйінен шығарған әсерінен кейін тепе-теңдіктің бастапқы қалпына қайта келу қасиеті.
Түзу сызықты жүйелердің орнықтылығы - жүйелердің кейітуші сигналдарды қабылдағаннан кейін қайта қалпына келу мүмкіндігі. Жүйе орнықтылығы олардың эксплуатациялану мүмкіндігін сипаттайды.
Жүйелерді күйіне қарай үш түрге бөлуге болады. Мысал ретінде механикалық шардың аналогын қарастырамыз. Шарға күш салғаннан кейін оның күйін (состояние) зерттейміз.
а б в
а) Шар бірнеше тербелістен кейін шұңқырдың түбіндегі берілген күйіне қайта қайтып оралады, яғни жүйе орныққан. Бұндай жүйе үшін, кері қайтудың сөніп бара жатқан (үйлес) үрдісі сәйкес келеді.
б) Шар берілген күйіне қайта оралмай, одан алысқа кете береді, яғни еркін қозғалыс тарамдалған (үйлеспеген) мінезге ие. Бұл орнықтырылмаған жүйе.
в) Шар, x әсерін алып тастағаннан кейін, бастапқы күйіне оралмай, ары қарай жылжымай, тепе – теңдіктің жаңа күйінде қалады. Бұл бейтарап (нейтрал) жүйе. Осыған орай, орнықтылық - жүйенің еркін қозғалысының сипаттамасымен анықталады.
Орнықтылықтың физикалық белгісі бойынша: егер өтпелі үрдістің еркін құрастырушысы yер(t) уақыт өскен сайын нөлге ұмтылса жүйе орнықты, егер ол шексіздікке ұмтылса онда орнықсыз, ал егер ол кейбір тұрақты шамаларға ұмтылса, онда оны бейтарап жүйе деп атайды [3].
Дебиет
1 Теория линейных систем автоматического регулирования: методические указания к выполнению лабораторных занятий для студентов специальности 050702/сост. В.А. Бороденко, А.Б. Жантлесова. – Павлодар: Кереку, 2008. – 66 с.
2 Бекбаев.А.Б., Сулеев Д., Хисаров Б. Автоматты реттеу теориясы. - Алматы, Дәуір, 2005ж.
3 Бороденко В.А. Практический курс теории линейных систем автоматического регулирования. – Павлодар: Кереку, 2007. – 260 с.
4 Ерофеев А.А. Теория автоматического управления. – 2-е изд., перераб. и доп. – СПб.: Политехника, 2005. – 302с.
5 Сборник задач по теории автоматического регулирования и управления / под ред. В.А. Бесекерского. – 5-е изд. – М.: Наука, 1978. – 512 с.
6 Электрические системы. Математические задачи электроэнергетики: учебник для студентов вузов / под ред. В. А. Веникова. – 2-е изд., перераб. и доп. – М.: Высш. школа, 1981. – 288 с.
7 Бекбаев А.Б. Автоматика және өндірістік процестерді автоматтандыру. - Алматы. «Білім» 1995ж.
А.Б. Уахитова, Ж.Ж. Байгузова, М.С. Макажанов
Теруге жіберілді 02.10.2014ж. Басуға қол қойылды 30.12.2014ж.
Пішіні 60х84 1/16 Тапсырыс № 293
