Түбірлік бағалау жүйе полюстері мен нөлдерінің комплекстік жазықтықта орналасуының өтпелі үрдіс түріне деген әсерін қарастырады. Реттеу сапасын тек орнықты жүйелер үшін ғана бағалайды.
Егер басқа түбірлердің әсерін елемейтін болсақ (қалған түбірлер жорамал осьтен 5-10 есе қашықтықта орналасқан) 
, онда жорамал оське жақын орналасқан түбірлер басым түбірлер деп аталады.
Жорамал осьтен оған жақын орналасқан сипаттамалық теңдеудің түбіріне дейінгі ара қашықтық (комплекстік түйіндес түбірлер жұбы) орнықтылық дәрежесі (αmin немесе η) деп аталады, ол жүйенің тез әрекет етуін (быстродействие) сипаттайды. Модуль бойынша түбірдің жорамал бөлігінің нақты бөлігіне максимал қатынасы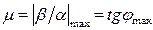 
, жүйенің тербелмелік дәрежесі деп аталады.
Реттеу сапасының негізгі көрсеткіштеріне реттеу мерзімі (үрдістің ұзақтығы) және қайта реттеу (өтпелі үрдіс кезіндегі тербеліс қарқыны) жатады. Реттеу мерзімін t рет бағалау үшін, алдымен жүйе орнықтылығының дәрежесін αmin немесе η табады, осыдан ∆=5 % қателігі кезінде:
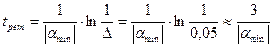
Қайта реттеуді (() бағалау үшін, алдымен жүйенің тербелмелік дәрежесін μ, содан кейін қайта реттеу мәнін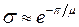 
анықтайды. Комплекстік түбірлердің бірнеше жұптары болған кезінде тербелмелік дәрежесінің μ максималды мәні, оң жорамал жартылай осьі бойынша координат басынан жүргізілген және сағат бағытына қарсы айналатын сәулеге бірінші кездесетін түбірде болады. Комплекстік түбірлердің бір ғана (негізгі) жұбы болған кезінде таңдау қажеттілігі керек емес.
Тұйықталған жүйенің сипаттамалық теңдеуінің парамтетрлерінің бірін 0-ден ∞-ке дейін өзгерту кезінде, сипаттамалық теңдеудің түбірлері арқылы комплекстік жазықтықта бейнеленген траекториялардың жиынтығы – түбірлі годограф деп аталады [3].
Бағалауды, әдетте тұйықталған жүйе үшін жасағандықтан, оның сипаттамалық теңдеуіне ажыратылған (тұйықталмаған) жүйенің нөлдері де, полюстері де енгізіледі. Егер 
, онда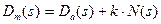 
.
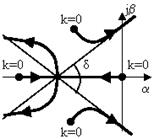
| Көбінесе реттегіштің k – күшейткіш коэффициентін өзгерте отырып, оның әрбір мәні үшін түбірлерін анықтап, оларды комплекстік жазықтықта бейнелейді. Түбірлі годографты салу кезінде оның төменде келтірілген қасиеттерін ескеру қажет: |
- түбірлі годографтың тармақтарының саны сипаттамалық теңдеудің дәрежесіне тең;
- түбірлі годографтың комплекстік бөліктерінің тармақтары нақты осьіне қатысты симметриялы;
- нақты осьіндегі тармақтардың ажырау нүктелері сипаттамалық теңдеудің еселі нақты түбірлеріне сәйкес келеді;
- жүйенің күшейткіш коэффициенті k нөлге ұмтылған кезінде, түбірлер траекториясы тұйықталмаған жүйенің беріліс функциясының полюстерінде басталады;
- жүйенің күшейткіш коэффициенті k шексіздікке ұмтылған кезінде, m түбірлер траекториясы, тұйықталмаған жүйенің беріліс функциясының нөлдерінде аяқталады, ал қалған n-m тармақтары асимптотикалық түрде шексіздікке кетеді. Мұндағы m – бұл жүйенің беріліс функциясының алымындағы полиномының реті, ал n – бөліміндегі полиномының ретін білдіреді.
