КОНЕЧНАЯ ЦЕЛЬ ЗАДАНИЯ:
I. На основе табличных данных о термодинамических свойствах веществ в стандартных условиях уметь рассчитать:
1. Тепловой эффект химической реакции при постоянном давлении
(DН0r 298) и при постоянном объеме (DU0r 298).
2. Тепловой эффект реакции при постоянном давлении и любой температуре (DН0r Т), если в интервале температур от 298 до ТК теплоемкости участников реакции постоянны.
3. Изменение энергии Гибсса (DG 0r 298) и энергии Гельмгольца (DF0r 298) в химической реакции.
II. По значению DН0r 298 уметь сделать вывод о том, является ли реакция в прямом направлении экзотермической или эндотермической. Ответ обосновать.
III. По значению DG0r 298 уметь сделать вывод, в каком направлении реакция при стандартных условиях протекает самопроизвольно. Ответ обосновать.
Задание 1. Вычислите, используя данные таблицы №3, DН0r 298, DU0r 298, DG0r 298, DF0r 298 для реакции, уравнение которой приведено в таблице №1. Какими являются реакции в прямом направлении: экзотермическими или эндотермическими? В каком направлении протекают реакции самопроизвольно? Ответ обосновать.
Таблица 1
| № варианта | Реакция |
| 2HCl(г) ® H2(г) + Cl2(г) | |
| Fe3O4(т) + 4H2(г) ® 3Fe(т) + 4H2O(г) | |
| CaC2 + 2H2O(ж) ® Ca(OH)2(т) + C2H2(г) | |
| CH3CHO(г) + H2(г) ® C2H5OH(ж) | |
| C2H5OH(ж) ® C2H4(г) + H2O(ж) | |
| C2H6(г) ® C2H4(г) + H2(г) | |
| 2H2(г) + CO(г) ® CH3OH(г) | |
| C(т) + H2O(г) ® CO(г) + H2(г) | |
| CO2(г) + 4H2(г) ® CH4(г) +2H2O(г) | |
| CH4(г) + CO2(г) ® 2CO(г) + 2H2(г) | |
| CO(г) + H2O(г) ® CO2(г) + H2(г) | |
| CO(г) + 3H2(г) ® CH4(г) + H2O(г) | |
| CaC2(т) + 3CO(г) ® CaCO3(т) + 4C(т) | |
| 2SO2(г) + O2 ® 2SO3(г) | |
| 2NO2 (г) ® 2NO(г) + O2(г) |
Задание 2. Определите тепловой эффект реакции, уравнение которой приведено в таблице №2, при температуре 500 и 700 К и давлении 1,0133 105 Па, используя уравнение Кирхгофа для узкого интервала температур. Для решения задачи использовать данные таблицы №3.
Таблица 2
| № варианта | Реакция |
| 2HCl(г) ® H2(г) + Cl2(г) | |
| NH4Cl(т) ® NH3(г) + HCl(г) | |
| 2NO2 (г) ® 2NO(г) + O2(г) | |
| N2O4 (г) ® 2NO2(г) | |
| Mg(OH)2(т) ® MgO(т) + H2O(г) | |
| 2SO2(г) + O2(г) ® 2SO3(г) | |
| SO2(г) + Cl2(г) ® SO2Cl2(ж) | |
| CO(г) + 3H2(г) ® CH4(г) + H2O(г) | |
| CO2(г) + 4H2(г) ® CH4(г) +2H2O(г) | |
| CH4(г) + CO2(г) ® 2CO(г) + 2H2(г) | |
| CO(г) + Cl2(г) ® COCl2(г) | |
| 2CO2(г) ® 2CO(г) + O2(г) | |
| C2H5OH(г) ® C2H4(г) + H2O(г) | |
| CH3CHO(г) + H2(г) ® C2H5OH(г) | |
| CO(г) + Cl2(г) ® COCl2(г) |
Для выполнения задания использовать следующие закономерности:
1. DНr0 = S(DnНr0)прод – S(DnНr0)исх
2. DНr0 = DUr0 + DnRT
Dn – изменение числа молей газообразных веществ в ходе реакции
R = 8,31Ч10–3 кДж/моль
Т = 298 К
3. DGr0 = DНr0 – TDSr0; DFr0 = DUr0 – TDSr0
4. DGr0 = S(nDGr0)прод – S(nDGr0)исх
5. DSr0 = S(nS0)прод – S(nS0)исх
6. DHr0T2 = DHr0T1 + ΔCp(T2 – T1)
7. DCp0 = S(nCp0)прод – S(nCp0)исх
Таблица 3
ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА НЕКОТОРЫХ ВЕЩЕСТВ
В СТАНДАРТНЫХ УСЛОВИЯХ ПРИ 298 К
| ВЕЩЕСТВО | DHr0, кДж/моль | DSr0, Дж/мольК | DGr0, кДж/моль | Cp0, Дж/мольК |
| Н2(г) | 130,52 | 28,28 | ||
| О2(г) | 205,04 | 29,37 | ||
| Cl2(г) | 222,98 | 33,93 | ||
| С(т) | 5,74 | 8,54 | ||
| Fe (т) | 27,15 | 24,98 | ||
| Fe3O4(т) | —1117,13 | 146,19 | —1014,17 | 150,79 |
| MgСO3(т) | —1095,85 | 65,10 | —1012,15 | 76,11 |
| MgO(т) | — 601,49 | 27,07 | — 569,27 | 37,20 |
| Mg(OH)2(т) | — 924,66 | 63,10 | — 833,75 | 76,99 |
| NO(г) | 91,26 | 210,64 | 87,58 | 29,86 |
| NО2(г) | 34,19 | 240,06 | 52,29 | 36,66 |
| N2О4(г) | 11,11 | 304,35 | 99,68 | 79,16 |
| NН3(г) | — 45,94 | 192,66 | — 16,48 | 35,16 |
| NН4Cl(т) | — 314,22 | 95,81 | — 203,22 | 84,10 |
| SО2(г) | — 296,90 | 248,07 | — 300,21 | 39,87 |
| SО3(г) | — 395,85 | 256,69 | — 371,17 | 50,09 |
| SО2Cl2(ж) | — 394,13 | 216,31 | — 321,49 | 133,89 |
| СаС2(т) | — 795,92 | 108,37 | — 749,34 | 72,59 |
| СаО(т) | — 635,09 | 38,07 | — 603,46 | 42,05 |
| Са(ОН)2(т) | — 985,12 | 83,39 | — 897,52 | 87,49 |
| СаСО3(т) | —1206,83 | 91,71 | —1128,35 | 83,47 |
| СО(г) | — 110,53 | 197,55 | — 137,15 | 29,14 |
| СО2(г) | — 393,51 | 213,66 | — 394,37 | 37,11 |
| Н2О(г) | — 241,81 | 188,72 | — 228,61 | 33,61 |
| HCl(г) | — 92,31 | 186,79 | — 95,30 | 29,14 |
| Н2О(ж) | — 285,83 | 69,95 | — 237,23 | 75,30 |
| СН4(г) | — 74,85 | 186,27 | — 50,85 | 35,71 |
| С2Н2(г) | 226,75 | 200,82 | 209,21 | 43,93 |
| С2Н4(г) | 52,30 | 219,45 | 68,14 | 43,56 |
| С2Н6(г) | — 84,67 | 229,49 | — 32, 93 | 52,64 |
| СН3СНО(г) | — 166,00 | 264,20 | — 132,95 | 54,64 |
| С2Н5ОН(г) | — 234,80 | 281,38 | — 167,96 | 65,75 |
| С2Н5ОН(ж) | — 276,98 | 160,67 | — 174,15 | 111,96 |
| СОСl2(г) | — 219,50 | 283,64 | — 205,31 | 57,76 |
| СН3ОН(г) | — 201,00 | 239,76 | — 162,38 | 44,13 |
| С6Н6(г) | 82,93 | 269,20 | 129,68 | 81,67 |
| С6Н6(ж) | 49,03 | 173,26 | 124,38 | 135,14 |
| С6Н12(г) | — 123,14 | 298,24 | 31,70 | 106,27 |
З А Н Я Т И Е № 8
Т Е М А: «ПРАВИЛО ФАЗ ГИББСА. ФИЗИКО-ХИМИЧЕСКИЙ АНАЛИЗ».
I. МОТИВАЦИЯ ЦЕЛИ: Физико-химический анализ как самостоятельный раздел физической химии позволяет изучать свойства различных многофазных и многокомпонентных систем на основе построения и анализа диаграмм состояния. Такой подход позволяет решать важные для практических целей вопросы о составе равновесно сосуществующих фаз, их массовых соотношениях, условиях фазовых превращений и возможностях выделения чистых компонентов из их смесей.
Теория процессов фазовых превращений, таких как испарение-конденсация, плавление-кристаллизация, взаимная растворимость жидкостей, распределение третьего компонента между двумя несмешивающимися фазами служит обоснованием практического использования в фармации многих физико-химических методов исследования и разделения многокомпонентных смесей, а также методов получения чистых веществ.
Изучаемые в этом разделе теоретические закономерности позволяют оценить возможности, границы применения и оптимальные условия проведения таких широко используемых в фармации методов, как экстрагирование, перегонка, ректификация, перекристаллизация, перегонка с водяным паром.
В разработку данного раздела физической химии существенный вклад внесен работами выдающихся отечественных ученых, таких как Д.И. Менделеев, И.А. Каблуков, а также Д.П. Коновалов (основы теории перегонки жидких смесей), Н.С. Курнаков (основы физико-химического анализа, пирометрический анализ), Н.А. Шилов и Л.А. Лепинь (распределение растворенных веществ между жидкими фазами), В.Ф. Алексеев (взаимная растворимость жидкостей).
Физико-химический анализ базируется на рассмотрении процессов фазовых превращений как переходах от одного качественного состояния к другому в форме скачка и направлен на изучение взаимосвязи дискретных и непрерывных свойств материи в многофазных многокомпонентных системах.
II. ЦЕЛЬ САМОПОДГОТОВКИ:
Усвоить понятия “фаза”, “компонент”, “степень свободы”, правило фаз Гиббса, уравнение Клаузиуса-Клапейрона, назначение физико-химического анализа, принципы Курнакова, диаграммы состояния однокомпонентных систем.
III. ИСХОДНЫЙ УРОВЕНЬ ЗНАНИЙ:
Агрегатные состояния вещества, фазовые превращения, законы термодинамики, газовые законы.
IV.П Л А Н И З У Ч Е Н ИЯ Т Е М Ы:
1. Основные понятия: «фаза», «составляющий компонент», «число независимых компонентов», «число степеней свободы», «фигуративная точка».
2. Классификация систем по числу компонентов, числу фаз и числу степеней свободы.
3. Фазовый переход. Фазовые переходы I рода – плавление, кристаллизация, испарение, возгонка, конденсация.
4. Фазовое равновесие. Условия фазового равновесия.
5. Правило фаз Гиббса, его вывод.
6. Расчет максимального числа степеней свободы для системы и максимального числа фаз, которые могут находиться в равновесии в системе с заданным числом компонентов.
7. Понятие о физико-химическом анализе. Принципы физико-химического анализа Н.С. Курнакова: непрерывности и геометрического соответствия. Диаграмма состояния.
8. Диаграмма состояния воды: общий вид, характеристика линий и полей диаграммы. Тройная точка.
9. Диаграмма состояния серы: общий вид, характеристика линий полей и тройных точек диаграммы.
10. Число степеней свободы для однокомпонентных систем (воды, серы, фосфора), которым соответствуют фигуративные точки, лежащие на полях, линиях, в тройной (тройных) точках.
11. Уравнение Клапейрона-Клаузиуса.
V. Л И Т Е Р А Т У Р А:
1. Евстратова К. И., Купина Н. А., Малахова Е.Е. Физическая и коллоидная химия М., 1990, с. 61-68.
2. Киреев В. А. Краткий курс физической химии М. 1978, с.238-253.
3. Стромберг А. Г., Семченко Д.П., Физическая и коллоидная химия, М., 1999, с. 152-162.
4.Лекционный материал.
VI. В О П Р О С Ы Д Л Я С А М О К О Н Т Р О Л Я:
1. Приведите определение понятий: "фаза", "составляющий компонент", "число независимых компонентов", "число степеней свободы", "фазовый переход", "фазовое равновесие", "фигуративная точка".
2. Правило фаз Гиббса - словесная формулировка. Запишите уравнение правила фаз Гиббса для системы, на которую:
- из внешних условий влияют температура и давление;
- из внешних условий влияет только температура;
- влияет "n" внешних условий.
3. Система состоит из раствора сульфатов калия и натрия в воде, кристаллов сульфата калия и кристаллов сульфата натрия.
а) Чему равно число независимых компонентов в системе?
б) Сколько и какие фазы образуют систему?
в) Приведите вид уравнения правила фаз Гиббса, выполняемого в данной системе. Рассчитайте число степей свободы.
4. Система представляет собой жидкий расплав солей хлорида натрия и нитрата калия, находящихся в равновесии с кристаллами нитрата калия. Между солями в расплаве возможна реакция:
NaCl + KNO3 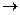 KCl + NaNO3
KCl + NaNO3
а) Чему равно число независимых компонентов в системе?
б) Сколько и какие фазы образуют систему?
в) Приведите вид уравнения правила фаз Гиббса, выполняемого в данной системе. Рассчитайте число степеней свободы.
5. Вычислите наибольшее число степеней свободы для однокомпонентной системы (вода) при n=2.
6. Приведите уравнение для расчета максимального числа фаз в однокомпонентной системе (вода) при n=2.
7. Виды фазовых переходов.
8. Уравнение Клапейрона и Клапейрона-Клаузиуса.
9. Тепловые эффекты фазовых переходов.
10. Сформулируйте принципы физико-химического анализа Н.С.Курнакова: принцип непрерывности и принцип соответствия.
11. Дайте определение "диаграмме состояния".
12. Диаграмма состояния воды имеет вид:

- Как называются линии ОА, ОВ и ОС? Зависимость между какими свойствами отражает каждая линия?
- Как называются поля I, II, III? Что представляет собой система, характеризуемая любой фигуративной точкой каждого поля?
- Каков геометрический образ комплекса из трех равновесных фаз? Перечислите эти фазы.
- Как называется фигуративная точка "О"? Почему?
- Определите число степеней свободы для систем, которым соответствуют фигуративные точки "d" и "О".
13. Запишите уравнение Клаузиуса-Клапейрона, обозначив входящие в него величины.
14. Приведите вид уравнений Клаузиуса-Клапейрона применительно к процессам:
- испарения,
- плавления,
- возгонки, обозначив входящие в них величины.
15. Приведите общий вид диаграммы состояния серы. Охарактеризуйте линии, поля, тройные точки на данной диаграмме.
VII. ОБЯЗАТЕЛЬНЫЕ ДЛЯ ВЫПОЛНЕНИЯ ЗАДАНИЯ:
Примеры решения задач
Пример 6-1. Рассчитать изменение давления, необходимое для изменения температуры плавления льда на 1o C. При 0o C энтальпия плавления льда равна 333.5 Дж. г–1, удельные объемы жидкой воды и льда равны V ж. = 1.0002 см3. г–1 и V тв. = 1.0908 см3. г–1.
Решение. Изменение объема при плавлении льда равно
V ж. – V тв. = 1.0002 – 1.0908 = –0.0906 см3. г–1 = –9.06 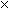 10–8 м3. г–1.
10–8 м3. г–1.
 = –1.348
= –1.348 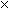 107 (Па. К–1) = –133 атм. К–1.
107 (Па. К–1) = –133 атм. К–1.
Таким образом, при повышении давления на 133 атм температура плавления льда понижается на 1 градус. Знак "минус" показывает, что при повышении давления температура плавления понижается.
Ответ.  P = 133 атм.
P = 133 атм.
Пример 6-2. Рассчитать давление пара жидкого брома при 25o C.  fGo газообразного брома равна 3.110 кДж. моль–1.
fGo газообразного брома равна 3.110 кДж. моль–1.
Решение.  исп Go брома равно
исп Go брома равно  fGo [Br2 (г)] = 3110 Дж. моль–1.
fGo [Br2 (г)] = 3110 Дж. моль–1.
 исп Go =
исп Go =  , откуда P = 0.2852 атм.
, откуда P = 0.2852 атм.
Ответ. P = 0.2852 атм.
Пример 6-3. Рассчитать давление, при котором графит и алмаз находятся в равновесии при 25o C.  fGo алмаза равна 2.900 кДж. моль–1. Считать плотности графита и алмаза равными 2.25 и 3.51 г. см–3 соответственно и не зависящими от давления.
fGo алмаза равна 2.900 кДж. моль–1. Считать плотности графита и алмаза равными 2.25 и 3.51 г. см–3 соответственно и не зависящими от давления.
Решение. Изменение объема при переходе от графита к алмазу равно
 V = 12.
V = 12. 
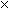 10–6 = –1.91
10–6 = –1.91 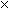 10–6 м3. моль–1
10–6 м3. моль–1
При начальном давлении P 1 разность мольных энергий Гиббса  G 1 = 2900 Дж. моль–1, а при конечном давлении P 2 разность
G 1 = 2900 Дж. моль–1, а при конечном давлении P 2 разность  G 2 =0.
G 2 =0.
Поскольку 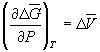 , то
, то 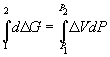 =
=  G 2 –
G 2 –  G 1 =
G 1 =  V (P 2 – P 1).
V (P 2 – P 1).
Отсюда P 2 =  = 1.52
= 1.52 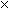 109 Па = 1.5
109 Па = 1.5  104 атм.
104 атм.
Ответ. P = 1.5  104 атм.
104 атм.
Пример 6-4. Температура кипения бензола при давлении 1 атм равна 80.1o C. Оценить давление пара бензола при 25o C.
Решение. Давление пара бензола при T 1 = 353.3 K равно P 1 = 1 атм. По правилу Трутона  исп H = 88. 353.3 = 31.1 кДж. моль–1. Подставим эти данные в уравнение (6.9). Получим:
исп H = 88. 353.3 = 31.1 кДж. моль–1. Подставим эти данные в уравнение (6.9). Получим:
 , откуда P 2 = 0.141 атм.
, откуда P 2 = 0.141 атм.
Ответ. P = 0.141 атм.
1. Рассчитать давление, при котором две формы CaCO3 – кальцит и арагонит – находятся в равновесии при 25o C.  fGo кальцита и арагонита при 25o C равны –1128.79 и –1127.75 кДж. моль–1 соответственно. Считать, что плотности кальцита и арагонита равны 2.71 и 2.93 г. см–3 соответственно и не зависят от давления.
fGo кальцита и арагонита при 25o C равны –1128.79 и –1127.75 кДж. моль–1 соответственно. Считать, что плотности кальцита и арагонита равны 2.71 и 2.93 г. см–3 соответственно и не зависят от давления.
2. Рассчитать температуру, при которой две формы CaCO3 – кальцит и арагонит – находятся в равновесии при давлении 1 атм. При 25o C  fGo кальцита и арагонита равны –1128.79 и –1127.75 кДж. моль–1 соответственно,
fGo кальцита и арагонита равны –1128.79 и –1127.75 кДж. моль–1 соответственно,  fHo равны–1206.92 и –1207.13 кДж. моль–1 соответственно. Считать, что
fHo равны–1206.92 и –1207.13 кДж. моль–1 соответственно. Считать, что  C P = 0.
C P = 0.
3.  fGo жидкой и газообразной воды при 25o C равны –237.129 и –228.572 кДж. моль–1 соответственно. Рассчитать давление пара воды при 25o C.
fGo жидкой и газообразной воды при 25o C равны –237.129 и –228.572 кДж. моль–1 соответственно. Рассчитать давление пара воды при 25o C.
4. Плотности жидкого и твердого олова при температуре плавления (231.9o C) равны 6.980 г. см–3 и 7.184 г. см–3 соответственно. Энтальпия плавления олова равна 1.690 ккал. моль–1. Определить температуру плавления олова под давлением 500 атм. Молярная масса олова равна 118.7 г. моль–1.
5. При замерзании бензола (5.5oC) его плотность изменяется от 0.879 г. см–3 до 0.891 г. см–3. Энтальпия плавления равна 10.59 кДж. моль–1. Определить температуру плавления бензола при давлении 1000 атм.
6. Плотности жидкой и твердой ртути при температуре плавления
(–38.87oC) равны 13.690 и 14.193 г. см–3 соответственно. Энтальпия плавления ртути равна 2.33 кал. г–1. Определить температуру плавления ртути при давлении 3000 атм.
7. Температура кипения жидкого метанола равна 34.7 o C при давлении 200 мм рт. ст. и 49.9 o C при давлении 400 мм рт. ст. Найти температуру кипения метанола при нормальном давлении.
8. Давление пара диэтилового эфира при 10o C равно 286.8 мм рт. ст., а при 20o C – 432.8 мм рт. ст. Определить мольную энтальпию испарения и нормальную температуру кипения эфира.
9. Давление пара дихлорметана при 24.1oC равно 400 Торр, а его энтальпия испарения равна 28.7 кДж. моль–1. Рассчитать температуру, при которой давление пара будет равно 500 Торр.
10. Давление пара твердого CO2 равно 133 Па при –134.3o C и 2660 Па при –114.4 o C. Рассчитать энтальпию возгонки.
11. Давление пара (Торр) жидкости в интервале температур 200 – 260 K описывается уравнением:
ln p = 16.255 – 2501.8 / T.
Рассчитать энтальпию испарения и нормальную точку кипения жидкости.
12. Давление пара (Торр) жидкого бензола C6H6 между 10oC и 80oC описывается уравнением:
lg p = 7.960 – 1780 / T.
Рассчитать энтальпию испарения и нормальную точку кипения бензола.
13. Давление пара жидкого нафталина C10H8 равно 10 Торр при 85.8oC и 40 Торр при 119.3oC. Определить энтальпию испарения, нормальную точку кипения и энтропию испарения в нормальной точке кипения.
14. Нормальная точка кипения гексана равна 69.0 o C. Оценить а) мольную энтальпию испарения и б) давление пара гексана при 25 o C и 60 o C.
15. При 0oC энтальпии испарения и плавления воды равны 595 и 79.7 кал. г–1 соответственно. Давление пара воды при 0oC равно 4.58 мм рт. ст. Рассчитать давление пара льда при –15oC, считая, что изменение энтальпии не зависит от температуры.
16. Рассчитать температуру кипения воды на вершине Эвереста (высота 8850 м). Энтальпию испарения воды считать равной 40.67 кДж. моль–1. Для расчета атмосферного давления на вершине воспользоваться барометрической формулой.
17. Уксусная кислота имеет следующие давления насыщенного пара:
| T, K | |||
| P, мм. рт. ст. |
18. Определить молярную массу уксусной кислоты в паре, если известно, что  исп H = 24.35 кДж. моль–1.
исп H = 24.35 кДж. моль–1.
19. Давление пара (в мм рт. ст.) твердого и жидкого SO2 выражается уравнениями
lg P (тв) = 10.5916 – 1871.2/ T
lg P (ж) = 8.3186 – 1425.7/ T
Рассчитать температуру, давление и  пл H SO2 в тройной точке.
пл H SO2 в тройной точке.
20. Давление пара (в мм рт. ст.) над твердым и жидким UF6 выражается уравнениями
lg P (тв) = 10.648 – 2559.5/ T
lg P (ж) = 7.540 – 1511.3/ T
Рассчитать температуру, давление и  пл H UF6 в тройной точке.
пл H UF6 в тройной точке.
21. Давление пара над твердым Cl2 равно 352 Па при –112oC и 35 Па при –126.5oC, а давление пара над жидким Cl2 равно 1590 Па при –100oC и 7830 Па при –80oC. Определить координаты тройной точки и  пл H Cl2.
пл H Cl2.
22. Давление пара над твердым C6H6 равно 299 Па при –30oC и 3270 Па при 0oC, а давление пара над жидким C6H6 равно 6170 Па при 10oC и 15800 Па при 30oC. Определить координаты тройной точки и  пл H C6H6.
пл H C6H6.
23. Давление пара над твердым SnBr4 равно 0.116 мм рт. ст. при 9.8 oC и 0.321 мм рт. ст. при 21.0 oC, а давление пара над жидким SnBr4 равно 0.764 мм рт. ст. при 30.7 oC и 1.493 мм рт. ст. при 41.4 oC. Определить координаты тройной точки и  пл H SnBr4.
пл H SnBr4.
24. Давление пара 2,2-диметилбутанола-1 (мм рт. ст.) выражается уравнением:
lg p = –4849.3/ T – 14.701 lg T + 53.1187.
Рассчитать а) нормальную точку кипения, б) энтальпию испарения в нормальной точке кипения, в) энтальпию испарения при 25o C.
25. Давление пара ртути (мм рт. ст.) в интервале 298 – 630 К выражается уравнением:
lg p = –3308/ T – 0.8 lg T + 10.373.
Рассчитать а) нормальную точку кипения ртути и б) энтальпию испарения ртути в нормальной точке кипения.
26. Рассчитать давление пара воды при 200o C, принимая, что а)  H исп = 40.67 кДж. моль–1 и не зависит от температуры; б)
H исп = 40.67 кДж. моль–1 и не зависит от температуры; б)  C p = –42 Дж. моль–1. К–1.
C p = –42 Дж. моль–1. К–1.
VIII. ПЛАН РАБОТЫ НА ПРЕДСТОЯЩЕМ ЗАНЯТИИ:
1. Контроль и коррекция выполнения домашнего задания.
2. Разбор основных теоретических вопросов темы.
3. Решение задач.
4. Тестовый контроль.
ЗАНЯТИЕ № 9
ТЕМА: ФАЗОВЫЕ РАВНОВЕСИЯ В СИСТЕМЕ ЖИДКОСТЬ-ЖИДКОСТЬ.
ОГРАНИЧЕННАЯ ВЗАИМНАЯ РАСТВОРИМОСТЬ ЖИДКОСТЕЙ.
I. МОТИВАЦИЯ ЦЕЛИ: Явление ограниченной растворимости может быть практически использовано для определения составов жидких лекарственных форм, не расслаивающихся при хранении. На принципе использования критической температуры растворения основаны некоторые виды качественного анализа. Путем увеличения концентрации одного из компонентов можно добиться его полного выделения из раствора. В ряде случаев такой способ разделения двойных смесей значительно проще фракционной перегонки.
II. ЦЕЛЬ САМОПОДГОТОВКИ:
1) уметь характеризовать состояние и свойства систем ограниченно растворимых жидкостей по диаграмме взаимной растворимости,
2) знать зависимость взаимной растворимости ограниченно растворимых жидкостей от температуры и состава.
III. ИСХОДНЫЙ УРОВЕНЬ ЗНАНИЙ: Зависимость растворимости жидкостей в жидкостях от различных факторов.
IV. ПЛАН ИЗУЧЕНИЯ МАТЕРИАЛА ТЕМЫ:
1. Классификация бинарных жидких смесей по способности компонентов растворяться друг в друге.
2. Ограниченная взаимная растворимость жидкостей, ее зависимость от температуры.
3. Диаграммы взаимной растворимости для систем с «верхней», «нижней», «верхней и нижней» критическими температурами растворения:
а) общий вид диаграмм;
б) кривая расслоения (растворимости);
в) области (поля) гомогенного и гетерогенного (двухфазного) состояния системы;
г) верхняя (нижняя) критическая температура растворения.
4. Анализ диаграмм взаимной растворимости с позиций правила фаз Гиббса.
5. Правило рычага, его использование при анализе диаграмм взаимной растворимости.
6. Правило прямолинейного диаметра В.Ф.Алексеева.
V. ЛИТЕРАТУРА:
1. Евстратова К. И., Купина Н. А., Малахова Е.Е. Физическая и коллоидная химия М., 1990, с. 68-82.
2. Киреев В. А. Краткий курс физической химии М. 1978, с.318-319.
3. Стромберг А. Г., Семченко Д.П. Физическая и коллоидная химия, М. 1999, с. 174-175.
4. Краснов К.С. Физическая химия, М. 2001, с. 442-444.
5. Лекционный материал.
VI. ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ:
1. Назовите три типа бинарных жидких систем, выделенных по способности жидкостей растворяться друг в друге.
2. К какому типу систем по способности компонентов растворяться друг в друге относятся жидкие системы:
а) вода - бензол;
б) вода - анилин;
в) вода - этиловый спирт?
3. Назовите три типа бинарных жидких систем, выделенных по характеру зависимости взаимной растворимости жидкостей от температуры.
4. К какому типу систем по характеру зависимости взаимной растворимости от температуры относятся системы:
а) диэтиламин - вода;
б) фенол - вода;
в) никотин - вода?
5. Как с повышением температуры изменяется растворимость в системах:
а) фенол - вода;
б) диэтиламин - вода?
6. Приведите диаграмму взаимной растворимости для системы:
а) фенол - вода;
б) диэтиламин - вода.
7. Дайте определение понятиям:
а) верхняя критическая температура растворения;
б) нижняя критическая температура растворения.
8. Диаграмма состояния ограниченно растворимых жидкостей А и В имеет вид:

а. К какому типу систем относится система, образованная компонентами А и В, ограниченно растворимыми дуг в друге?
б. Зависимость между какими свойствами устанавливает линия диаграммы (кривая расслоения)?
в. Укажите на диаграмме поля гомогенного и гетерогенного состояний системы.
9. Жидкость, состоящая из компонентов А и В, имеет валовый состав "х" (рис. пункта 8). Сделав построения, ответьте на вопросы:
а. Гомогенна или гетерогенна эта система при температурах t1 и t2?
б. Каков состав фаз для гетерогенного состояния системы?
в. Какова температура взаимной растворимости системы с валовым составом "х"?
10. Дайте определение понятиям "коннода", "сопряженные точки".
11. Охарактеризуйте системы, которым на диаграмме взаимной растворимости (рис. пункта 8) соответствуют фигуративные точки "c" и "d", по следующим свойствам:
а. Каков валовый состав системы? Какого компонента (А или В) в системе содержится больше?
б. Гомогенна или гетерогенна система?
в. Какова температура взаимной растворимости компонентов системы?
г. Как следует изменить температуру, чтобы гомогенная (гетерогенная) система перешла в гетерогенное (гомогенное) состояния?
д. Чему равно число степеней свободы системы?
е. Какой компонент (А или В) следует внести в гомогенную систему, чтобы в ней при заданной температуре началось расслоение (помутнение)?
12. Приведите формулировку правила Алексеева. Проиллюстрируйте его на диаграмме взаимной растворимости для систем с верхней или нижней критической температурой растворения.
13. Приведите формулировку правила рычага. Проиллюстрируйте выполнение этого правила на диаграмме взаимной растворимости.
14. Каково практическое использование правила рычага?
VII. ОБЯЗАТЕЛЬНЫЕ ДЛЯ ВЫПОЛНЕНИЯ ЗАДАНИЯ:
Примеры решения задач
Пример 9-1. По диаграмме состояния компонентов А и В

определите:
а) К каком типу относится данная система.
б) Что представляет собой система состава: 80% А и 20% В при температуре t'. Какими степенями свободы она обладает?
в) Каков состав равновесных фаз при температуре t'.
г) Как изменится растворимость с понижени45ем температуры.
д) Что представляет собой исходная система при температуре t", какими степенями свободы она обладает.
е) Какие изменения произойдут в системе при температуре t', если содержание компонента А изменится от 80% до 40%.
Решение
а) Изображенная диаграмма характерна для ограниченно смешивающихся жидкостей с нижней критической температурой смешивания.
б) Заданная система характеризуется фигуративной точкой а. При температуре t' она двухфазная. Составы фаз можно определить по точкам пересечения изотермы с кривыми растворимости (точки 1 и 2). Число степеней свободы c = k – Ф + 1 = 2 - 2 + 1 = 1, т. е. произвольно можно задать или температуру или концентрацию насыщенных растворов.
в) Составы фаз: фаза компонента А (точка 1) содержит 90% А и 10% В; фаза компонента В (точка 2) содержит 20% А и 80% В.
г) С понижением температуры растворимость компонентов растет.
д) При температуре t" система состава 80% А и 20% В становится однофазной и обладает двумя степенями свободы, т. е. произвольно можно задавать температуру и концентрацию.
е) При содержании А - 40% (фигуративная точка b) система остается двухфазной. Составы фаз не изменяются (они определяются точками 1 и 2), изменится весовое соотношение между фазами.
Пример 9-2. По диаграмме расслоения ограниченно смешивающихся жидкостей, указанной в таблице вариантов, определите:
а) К какому типу относится данная система.
б) Какова (или каковы) критическая температура рас слоения в данной системе.
в) Для указанного состава и температуры (состав системы № 1) число фаз, состав каждой фазы, число степеней свободы.
г) Массу каждой фазы в заданной точке, если масса системы составляет 10 кг.
д) Изменится ли число фаз, состав фаз, масса фаз, если состав системы изменится в изотермических условиях до указанного (состав системы № 2).
Варианты задания
| № вар. | № рис. | Состав системы №1 | t, °C | Состав системы №2, % масс. | |
| компонент | %, масс. | ||||
| g-коллидин | |||||
| - | |||||
| - | |||||
| - | |||||
| никотин | |||||
| - | |||||
| - | |||||
| - | |||||
| анилин | |||||
| - | |||||
| - | |||||
| - |

Рис. 1 Рис.2 Рис.3
VIII. ПЛАН РАБОТЫ НА ПРЕДСТОЯЩЕМ ЗАНЯТИИ:
1. Контроль и коррекция выполнения домашнего задания.
2. Разбор основных теоретических вопросов темы.
3. Решение задач.
4. Тестовый контроль.
5. Выполнение лабораторной работы:
«Построение диаграммы взаимной растворимости системы фенол-вода»
Лабораторная работа №5:
«Построение диаграммы взаимной растворимости системы фенол-вода»
1. Определить температуру взаимной растворимости для шести смесей фенол-вода состава:
| № смеси | ||||||
| Массовая для Фенола в смеси w, % |
а. Перемешав встряхиванием содержимое ампул со смесями, поместить их в водяную баню и при нагревании отметить температуру просветления (t1).
б. Не вынимая ампул из водяной бани, охладить их содержимое и отметить температуру (t2), при которой происходит расслоение системы (начинается помутнение).
в. Если разница в температурах t1 и t2 не превышает 2-40, найти среднее арифметическое этих температур и полученную величину принять за температуру взаимной растворимости. Если разница в температурах t1 и t2 больше 2-40, опыт повторить, уменьшив скорость нагревания и охлаждения.
2. Построить диаграмму взаимной растворимости.
В координатах t 0С – состав на поле графика нанести точки, отвечающие температуре взаимной растворимости для смесей каждого состава. Соединить точки плавной линией.
3. Установить критическую температуру взаимной растворимости (tкр) и охарактеризовать, к какому типу систем по влиянию температуры на растворимость относится система фенол-вода.
а. По правилу Алексеева найти точку (К) пересечения прямой, соединив середины двух произвольно выбранных коннод с кривой расслоения. Установить критическую температуру взаимной растворимости, найдя проекцию точки К на ось температур.
б. По наличию на диаграмме верхней или нижней критической температуры сделать вывод о типе системы фенол-вода и указать, как меняется растворимость воды и фенола друг в друге с повышением температуры.
4. Полученные в работе данные представить в виде таблицы:
| № смеси | Массовая доля бензойной кислоты в смеси w, % | Температура начала кристаллизации | Температура конца кристаллизации |
| 1. 2. 3. 4. 5. 6. |
ВОПРОСЫ ДЛЯ КОНТРОЛЯ УСВОЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ:
1. Почему для определения температуры расслоения определяют предварительно два значения?
2. Почему при определении необходимо постоянно встряхивать содержимое ампул?
3. Как называется кривая диаграммы взаимной растворимости?
4. Как на диаграмме взаимной растворимости находится критическая температура расслоения?
З А Н Я Т И Е № 10
Т Е М А: «БИНАРНЫЕ ЖИДКИЕ СМЕСИ С ПОЛНОЙ ВЗАИМНОЙ РАСТВОРИМОСТЬЮ. ЗАКОН РАУЛЯ. I-й ЗАКОН КОНОВАЛОВА»
I. МОТИВАЦИЯ ЦЕЛИ: Неограниченно растворимыми называют жидкости, которые могут растворяться друг в друге в любых соотношениях, образуя одну жидкую фазу. От состава образующегося раствора зависят его температура кипения, состав паровой фазы над раствором и давление насыщенных паров. Для изучения равновесия пар Û жидкий раствор применяют два типа диаграмм состояния:
1) диаграммы давление пара – состав (T = const);
2) диаграммы температура кипения – состав (p = const).
На практике для изучения равновесия пар – жидкий раствор чаще используются диаграммы температура – состав, называемые диаграммами кипения. Диаграммы кипения, как, впрочем, и другие диаграммы состояния позволяют довольно просто и быстро решать целый ряд практических задач, не прибегая к эксперименту. С помощью диаграмм состояния можно определить число и состав равновесных фаз при любой заданной температуре, количественные соотношения между фазами, выполнить различные расчеты, связанные с изменением состава системы и природы равновесных фаз.
Первый закон Коновалова характеризует соотношения между составами равновесных жидкости и пара и влияние добавления того или другого из компонентов на общее давление пара.
II. ЦЕЛЬ САМОПОДГОТОВКИ:
- усвоить содержание закона Рауля и знать свойства идеальных растворов и смесей с отклонениями от закона Рауля;
- знать формулировки и содержание I закона Коновалова;
- усвоить принцип построения диаграмм кипения бинарных смесей;
- уметь анализировать диаграммы кипения с позиции правила фаз и принципов Курнакова.
III. ИСХОДНЫЙ УРОВЕНЬ ЗНАНИЙ: Для усвоения материала темы необходимо знать следующие, изученные на предыдущем занятии, вопросы:
- правило фаз Гиббса;
- принципы построения и анализа диаграмм состояния;
- правило рычага;
- зависимость взаимной растворимости жидкостей от различных факторов;
- понятие об идеальных растворах.
IV. П Л А Н И З У Ч Е Н ИЯ Т Е М Ы:
1. Термодинамическое и молекулярно-кинетическое условия образования раствора.
2. Бинарные жидкие растворы летучих веществ. Закон Дальтона.
3. Идеальные, или простейшие системы, их свойства. Закон Рауля. Диаграмма зависимости общего и парциальных давлений насыщенного пара компонентов от состава идеального раствора.
4. Растворы с положительным и отрицательным отклонениями от закона Рауля, причины отклонений, свойства растворов. Диаграммы зависимости общего и парциальных давлений насыщенного пара компонентов от состава для растворов с положительным и отрицательным отклонением от закона Рауля.
5. Диаграммы кипения в координатах: температура-состав, давление-состав для идеальных смесей и систем с небольшими положительными и отрицательными отклонениями от закона Рауля:
а) общий вид диаграммы;
б) кривая жидкости и пара;
в) поле пара, жидкости и гетерогенного состояния системы.
6. I закон Коновалова: формулировка закона, его иллюстрация на диаграммах кипения.
7. Анализ диаграмм кипения с позиций правила фаз Гиббса.
8. Использование правила рычага при определении по диаграммам кипения масс пара и жидкости в равновесной гетерогенной системе.
IV. Л И Т Е Р А Т У Р А:
1. Евстратова К. И., Купина Н. А., Малахова Е.Е. Физическая и коллоидная химия М., 1990, с. 77-78, 82-84, 93-98.
2. Киреев В. А. Краткий курс физической химии М. 1978, с.300-313.
3. Стромберг А.Г., Семченко Д.П. Физическая химия М., 1999, с. 189-195, с. 210-216.
4. Краснов К.С. Физическая химия М., 2001, с. 444-448.
5. Лекционный материал.
VI. В О П Р О С Ы Д Л Я С А М О К О Н Т Р О Л Я:
1. Приведите словесную и математическую формулировки закона Дальтона.
2. Приведите словесную и математическую формулировки закона Рауля.
3. Какие растворы относятся к идеальным (определение)? Примеры идеальных растворов.
4. Перечислите свойства:
а. Идеальных растворов.
б. Растворов с положительным отклонением от закона Рауля.
в. Растворов с отрицательным отклонением от закона Рауля.
5. Приведите диаграмму зависимости общего и парциальных давлений насыщенного пара бинарных растворов от состава для:
а. Идеальных растворов.
б. Растворов с положительным отклонением от закона Рауля.
в. Растворов с отрицательным отклонением от закона Рауля.
5. Назовите кривые на рисунке 1


Рис.1. Рис.2
Укажите области пара и жидкости. Опишите, какие изменения будут происходить со смесью, состояние которой (состав и давление) выражается: а) точкой а, если давление уменьшать при постоянной температуре; б) точкой б, если давление увеличивать при постоянной температуре.
6 Диаграмма, изображенная на рисунке 1, относится к той же системе, что и диаграмма на рисунке 2. Объясните, почему на них различное расположение кривых. Как называются кривые на рисунке? Где располагаются области пара и жидкости?
7. Опишите, какие изменения будут происходить со смесью, состояние которой (состав - температура) выражается при постоянном давлении:
1) точкой а при повышении температуры или 2) точкой б при понижении температуры (рис. 2).
8. Приведите общий вид диаграммы кипения в координатах температура – состав для идеальных смесей и систем с небольшим положительным и отрицательным отклонениями от закона Рауля.
9. Как расположены по отношению друг к другу линии жидкости и пара на диаграммах кипения в координатах t°С - состав?
10. Какие свойства бинарного жидкого раствора можно определить, используя диаграмму кипения в координатах t°С - состав:
а. По линии жидкости;
б. По линии пара?
11. Приведите формулировку I закона Коновалова.
12. Диаграмма кипения бинарного жидкого раствора имеет вид:

а. Какое отклонение от закона Рауля наблюдается в растворах из компонентов А и В? Ответ обосновать.
б. Выделите на диаграмме линии и укажите, зависимость между какими свойствами устанавливает каждая их них.
в. Выделите на диаграмме поля и охарактеризуйте каждое.
13. Жидкость, состоящая из компонентов А и В, имеет валовый состав "х" (рис. пункта 12). Сделав построения, ответьте на вопросы:
а. При какой температуре смесь состава "х" закипит?
б. Каков состав первого пузырька пара?
в. Какого компонента - А или В в образовавшемся паре будет содержаться больше по сравнению с жидкостью состава "х"?
г. Сколько и каких фаз будет находиться в системе, если жидкость состава "х" нагреть до температуры t1?
д. При какой температуре жидкий раствор состава "х" полностью перейдет в пар?
е. Каков состав последней капли жидкости, перешедшей в пар?
14. Для систем, которым на диаграмме кипения (рис. пункта 12) соответствуют фигуративные точки K и N, установите:
а. Гомогенна или гетерогенна система.
б. Каков валовый состав системы?
в. Каков состав фаз (фазы)?
г. Чему равно число степеней свободы?
15. Проиллюстрируйте правило рычага на диаграмме кипения (рис. пункта 12).
16. Диаграмма кипения для бинарной жидкой системы из компонентов А и В имеет вид - рис. пункта 12. Приведите диаграмму кипения для этой системы в координатах давление – состав и укажите на ней линию жидкости и пара.
17. Докажите на основании закона Дальтона, что отношение молей компонентов А и В в парах (nА/nB) равно отношению их парциальных давлений (рА/рB).
VII. ОБЯЗАТЕЛЬНЫЕ ДЛЯ ВЫПОЛНЕНИЯ ЗАДАНИЯ:
1. Дорисуйте на диаграммах линию пара и определите в каждом случае тип диаграммы


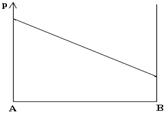
2. Ацетон и этиловый эфир неограниченно растворяются друг в друге. При 20 °С парциальные давления (мм рт.ст.)этих веществ над их смесями различного состава, выраженного в мольных %, приведены в таблице:
| cац, % | 5,20 | 12,71 | 24,90 | 45,7 | 61,2 | 66,6 | 84,2 | 93,6 | 97,9 | 99,6 | ||
| рац | ||||||||||||
| рэф |
1) По данным таблицы построить кривые зависимости парциальных давлений паров ацетона и эфира и общего давления пара от состава смеси. Является ли эта смесь идеальной?
2) Пользуясь диаграммой, определить:
а) парциальные и общее давление паров для эквимолекулярной смеси ацетона и эфира;
б) состав смеси, которая будет кипеть при давлении 290 мм pт.cт.
3) Построить кривые зависимости общего давления пара от состава жидкой смеси и состава пара.
4) Определить при каком давлении начнется кипение жидкой смеси, содержащей 30% (мольных) ацетона; каков состав равновесного с ней пара.
5) Определить при каком давлении начнется конденсация смеси, которая находится под давлением 200 мм pт. cт. и состоит из 70% ацетона и 30% эфира; каков состав первой капли конденсата.
6) Что собой представляет смесь из 55% ацетона и 45% эфира при давлении 340 мм рт.ст
3. Бензол и дихлорэтан образуют смеси, подчиняющиеся закону Рауля. При 40°С давления пара бензола и дихлорэтана соответственно равны 182,5 и 155,0 мм рт. ст. Вычислите при этой температуре парциальное давление насыщенных паров каждого компонента и общее давление смеси, содержащей: 1) 0,2 мольные доли бензола; 2) 500 г бензола и 500 г дихлорэтана.
4. Сероуглерод и четыреххлористый углерод, неограниченно растворимые друг в друге жидкости, образуют смеси, близкие к идеальным. При 40°С давление пара сероуглерода равно 616,7 мм рт.ст., а четыреххлористого углерода - 215,8 мм рт. ст. Вычислите при этой температуре общее и парциальные давления паров каждого компонента, равновесных со смесью, содержащей: 1) 30% (мольных) сероуглерода; 2) 90% по массе сероуглерода.
5. Бензол и хлорбензол образуют смеси, близкие к идеальным. При 80 °С давления пара бензола и хлорбензола соответственно равны 754 и 145 мм рт. ст. Вычислите: 1) состав смеси в мольных %, если парциальное давление бензола в два раза больше парциального давления хлорбензола; 2) состав пара, равновесного с этой смесью.
6. При 60 °С давления пара бензола и толуола соответственно равны 392,5 и 139,5 мм рт. ст. Смесь этих веществ практически идеальна. Вычислите ее состав в мольных процентах, если общее давление равновесного с ней пара равно 250 мм рт. ст. Каков состав пара над этой смесью?
7. Бензол и дихлорэтан неограниченно растворимы друг в друге. При 50 °С парциальные давления этих веществ над их смесями различного состава приведены в таблице:
| c, % C2H4Cl2 | 29,8 | 52,3 | 75,4 | 92,1 | |||
| p (C2H4Cl2) | 33,4 | 70,5 | 124,6 | 178,1 | 217,2 | 236,2 | |
| p (C6H6) | 232,9 | 188,5 | 127,4 | 65,8 | 21,5 |
1) Постройте по данным таблицы кривые зависимости парциальных давлений паров дихлорэтана и бензола и общего давления пара от состава жидкости. Можно ли смесь этих веществ считать идеальной?
2) Найдите, пользуясь диаграммой, парциальные давления и общее давление паров смесей, содержащих: а) 40% и б) 80% (мольных) дихлорэтана. Вычислите эти величины по закону Рауля. Сравните полученные результаты.
3) Определите состав смеси, которая кипит под давлением 250 мм рт. ст.
8. Для системы, рассмотренной в предыдущей задаче, используя данные таблицы:
а) вычислите общее давление пара, а также состав пара для составов смесей, приведенных в этой таблице;
б) по полученным данным постройте кривые зависимости общего давления пара от состава жидкости и состава пара;
в) определите, при каком давлении начнется конденсация смеси, находящейся под давлением 245 мм рт. ст. и состоящей из 40% дихлорэтана и 60% бензола.
Каков состав первой капли конденсата?
VIII. ПЛАН РАБОТЫ НА ПРЕДСТОЯЩЕМ ЗАНЯТИИ:
1. Контроль и коррекция выполнения домашнего задания.
2. Разбор основных теоретических вопросов темы.
3. Решение задач.
4. Тестовый контроль.
5. Выполнение лабораторной работы: «Определение концентрации спирта в настойках по температуре кипения»
Лабораторная работа №6
«Определение концентрации спирта в настойках по температуре кипения»
Температура кипения жидкости – это температура, при которой давление насыщенного пара над жидкостью (раствором заданного состава) равно внешнему (атмосферному давлению).
При заданном внешнем давлении температура кипения жидкости определяется ее природой или составом. Измеряя температуру кипения, можно проводить идентификацию жидкости, характеризовать ее чистоту, можно по температуре кипения определить состав бинарного раствора (например, определить массовую долю растворенного вещества в растворе).
При определении температуры кипения капиллярным методом необходимо для исследуемой жидкости отметить температуру, при которой прекращается выход пузырьков пара из капилляра и жидкость начинает заходить в капилляр. Этой температуре соответствует равенство давления насыщенного пара над жидкостью внешнему давлению. При этом капилляр, запаянный с одного конца и погруженный в исследуемую жидкость открытым концом, играет роль манометра.
УСТРОЙСТВО ПРИБОРА ДЛЯ ОПРЕДЕЛЕНИЯ ТЕМПЕРАТУРЫ КИПЕНИЯ КАПИЛЛЯРНЫМ МЕТОДОМ И ПОСЛЕДОВАТЕЛЬНОСТЬ РАБОТЫ С НИМ
Прибор состоит из внешней широкой пробирки, заполненной водой и играющей роль водяной бани, внутренней стеклянной трубки, заканчивающейся тонкостенным шариком, который заполняется исследуемой жидкостью, термометра и капилляра, запаянного с одного конца.
I. Широкую пробирку на 3/4 заполнить водой и закрепить на штативе.
II. Внутреннюю трубку заполнить до половины шарика испытуемой жидкостью. В жидкость внести капилляр (30 мм длины) открытым концом вниз. Обратить внимание на то, что жидкость не заходит в капилляр.
III. К внутренней трубке прикрепить термометр так, чтобы ртутный резервуар термометра находился на уровне испытуемой жидкости.
IV. Нагревать воду в пробирке над пламенем спиртовки при постоянном помешивании. Пронаблюдать выход пузырьков газа из капилляра – вначале это пузырьки воздуха, а затем, когда жидкость будет нагрета до температуры кипения – пузырьки паров жидкости. Нагревание прекратить, когда из открытого конца капилляра начнет выделяться быстрый поток пузырьков пара.
V. Дать бане остыть при постоянном помешивании. Обратить внимание на то, что по мере охлаждения системы скорость выхода пузырьков пара вследствие его конденсации в жидкость уменьшается. Когда выделение пузырьков из капилляра прекратится и жидкость начнет заходить в капилляр, сделать отсчет температуры, приняв ее за температуру кипения.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Физико-химическое определение понятию "температура кипения".
2. Практическое значение измерения температуры кипения.
3. Какая величина является непосредственно измеряемой в опыте при определении температуры кипения жидкости капиллярным методом?
4. Почему после погружения капилляра в жидкость открытым концом жидкость до ее нагревания не заходит в капилляр, а в конце опыта, после прекращения нагревания и охлаждения жидкости до температуры кипения, она заходит в капилляр?
5. Состав установки для определения температуры кипения капиллярным методом.
6. Назначение широкой пробирки в приборе. До какого объема она должна быть заполнена водой?
7. Сколько исследуемой жидкости следует внести во внутреннюю пробирку?
8. Назначение капилляра в приборе.
9. Каким концом погружается капилляр в жидкость?
10. Как должен быть расположен термометр при сборке прибора?
11. Основные этапы определения температуры кипения капиллярным методом.
12. В какой момент следует прекратить нагревание жидкости во внешнем сосуде? Почему?
13. Каков качественный состав пузырьков газа в момент прекращения нагревания?
14. Почему необходимо выполнить требование: нагревание и охлаждение жидкости во внешнем сосуде проводить при постоянном перемешивании жидкости?
15. Почему температуру, при которой жидкость заходит в капилляр, принимают за температуру кипения?
Ход выполнения работы
1. Измерить капиллярным методом температуру кипения растворов этилового спирта в воде с массовой долей спирта 25%, 50%, 75% и 96%.
Смотреть описание работы по теме «Определение температуры кипения жидкостей капиллярным методом».
2. Построить калибровочный график.
В координатах t0 – состав на поле графика нанести точки, отвечающие температурам кипения растворов этилового спирта в воде заданных составов. Соединить полученные точки плавной кривой.
3. Измерить температуру кипения спиртовой настойки неизвестного состава.
Смотреть описание работы по теме «Определение температуры кипения жидкостей капиллярным методом».
4. Определить концентрацию спирта в настойке, используя калибровочный график.
На оси «температура» отложить значение температуры кипения настойки и, используя прием интерполяции, по калибровочному графику определить массовую долю этилового спирта в настойке.
5. По зависимости температуры кипения водного раствора этилового спирта от состава определить тип отклонения от закона Рауля.
а. Соотнести вид калибровочного графика, отражающего зависимость температуры кипения растворов этилового спирта от состава и соответствующего линии жидкости (диаграммы кипения), к линейной зависимости.
б. Представить (мысленно) и описать вид зависимости давления насыщенного пара от состава в этой системе, также соотнеся ее к линейной зависимости.
в. Сделать вывод о том, какое отклонение от закона Рауля наблюдается в растворах этилового спирта.
З А Н Я Т И Е № 11
Т Е М А: «II-Й ЗАКОН КОНОВАЛОВА. АЗЕОТРОПНЫЕ СМЕСИ. ЗАКОНЫ ВРЕВСКОГО. ПЕРЕГОНКА».
I. МОТИВАЦИЯ ЦЕЛИ: Второй закон Коновалова относится к достаточно широко распространенным системам, образующих, так называемые, азеотропные смеси. Примером летучей смеси с азеотропом, характеризуемой минимумом на кривой температуры






