КУРСКИЙ ГОСУДАРСТВЕННЫЙ МЕДИЦИНСКИЙ УНИВЕРСИТЕТ
БИОТЕХНОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ
КАФЕДРА ФИЗИЧЕСКОЙ И КОЛЛОИДНОЙ ХИМИИ
ЗАДАНИЯ
ДЛЯ СТУДЕНТОВ БИОТЕХНОЛОГИЧЕСКОГО ФАКУЛЬТЕТА
НА САМОСТОЯТЕЛЬНУЮ ПОДГОТОВКУ
К ЗАНЯТИЯМ ПО ФИЗИЧЕСКОЙ ХИМИИ
ЧАСТЬ I
КУРСК - 2003 г.
| УДК. 541.1 ББК | Печатается по разрешению редакционно-издательского совета КГМУ |
Задания для студентов биотехнологического факультета на самостоятельную подготовку к занятиям по физической химии //Новиков В.В., Оксененко О.И. - Курск: КГМУ, 2003. –109с.
Настоящее пособие составлено по основным разделам физической химии. Включает перечень вопросов для усвоения материала, указана литература для самостоятельного изучения, подробно описаны лабораторные работы, даны типовые задачи и показаны примеры их решения.
Учебное пособие составлено в соответствии с единой методической системой, принятой в КГМУ, и с программой по физической химии для студентов биотехнологического факультета.
Составители: к.м.н., доцент В.В.Новиков, к.х.н., ст. преп. О.И. Оксененко.
Рецензент:
ISBN 5-7487-0692-Х ББК 24.5
ã В.В. Новиков, 2003
”Физическая химия есть наука, объясняющая на основании положений и опытов физики то, что происходит в смешанных телах при химических операциях…”
М.В. Ломоносов, 1752 г.
З А Н Я Т И Е №1
ТЕМА: «МЕСТО ФИЗИЧЕСКОЙ ХИМИИ В ПОДГОТОВКЕ СПЕЦИАЛИСТА БИОТЕХНОЛОГА. ОРГАНИЗАЦИЯ УЧЕБНОГО ПРОЦЕССА НА КАФЕДРЕ. ПРАВИЛА РАБОТЫ В ЛАБОРАТОРИИ. СПОСОБЫ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНОГО МАТЕРИАЛА»
I. МОТИВАЦИЯ ЦЕЛИ:
Приведенной цитате нашего великого соотечественника М.В. Ломоносова, основоположника многих наук, в том числе и физической химии, два с половиной столетия, но ее содержание справедливо и сегодня и определяет предмет физической химии.
Физическая химия является базовой дисциплиной, усвоение которой в значительной степени определяет становление высококвалифицированного специалиста-биотехнолога. Она способствует формированию научного и инженерного мышления у студентов, создает теоретическую основу для изучения коллоидной химии, биохимии, технологии лекарств, микробиологических процессов, а также физико-химических методов исследования и анализа биологически активных соединений.
При изучении теоретической части физической и коллоидной химии необходимо анализировать большой по объему и разнообразный по содержанию графический материал. Выполнение и оформление лабораторных работ на практических занятиях также предусматривает построение многих графиков, без которых, как правило, невозможно достижение конечной цели работы. Кроме того, одним из самостоятельных разделов дисциплины является физико-химический анализ, который основывается на изучении свойств систем по геометрическому облику диаграмм состояния и графиков.
Наряду с общеизвестными принципами построения таблиц и графиков анализ графического материала в физической химии имеет свои особенности. Поэтому для последующего изучения предмета необходимо знать правила и способы графической обработки экспериментального материала, а также методы его статистической обработки.
II. ЦЕЛЬ САМОПОДГОТОВКИ:
1. Получить первоначальное представление о структуре предмета, задачах и методах физической химии.
2. Усвоить общие принципы построения таблиц и графиков.
3. Овладеть способами расчета погрешностей эксперимента.
III. ИСХОДНЫЙ УРОВЕНЬ ЗНАНИЙ: Для усвоения данной темы студент должен знать:
1. Основные представления предмета общей химии.
2. Понятия: “аргумент”, “функция”, “система координат”.
3. Обозначение осей координат.
4. Графическую интерпретацию математических уравнений типа: y = ax, y = a + bx, y = axb, y = aex.
IV. ПЛАН ИЗУЧЕНИЯ ТЕМЫ:
1. Предмет и задачи физической химии
2. Методы физической химии.
3. Связь физической химии с другими науками. Значение физической химии для других химических дисциплин.
4. История развития физической химии.
5. Экспериментальные физико-химические методы исследования, их особенности.
6. Правила работы в лаборатории.
7. Таблицы и графики: их назначение и правила построения.
8. Ошибки измерений и статистическая обработка опытных данных.
V. ЛИТЕРАТУРА:
1. К.И. Евстратова, Н.А.Купина, Е.Е.Малахова Физическая и коллоидная химия. - М., 1990, с. 4-11.
2. В.А.Киреев Краткий курс физической химии.- М., 1978, с. 13-24.
3. К.С. Краснов Физическая химия. - М., Высшая школа, 2001, с. 6-8.
4. Е.В. Бугреева, К.И. Евстратова, Н.А. Купина и др. Практикум по физической и коллоидной химии. - М., Высшая школа, 1990, с. 4-10.
5. Лекционный материал.
6. Рекомендации по способам обработки экспериментального материала (см. приложение к занятию).
VI.ОБЯЗАТЕЛЬНЫЕ ДЛЯ ВЫПОЛНЕНИЯ ЗАДАНИЯ:
Задание 1.
При определении при 250С степени диссоциации масляной кислоты в растворах различной концентрации было установлено, что эквивалентная электрическая проводимость раствора (
) с концентрацией (С) 0,015 моль/л равна 12,48 Ом -1 моль-1 см2; с концентрацией 0,02 моль/л - 10,53
Ом –1 моль-1 см2; а с концентрацией 0,01 моль/л - 15,2 Ом -1 моль-1 см2. Эквивалентная электрическая проводимость раствора масляной кислоты при бесконечном разведении (
) равна 390,1 Ом -1 моль-1 см2.
1. Пользуясь формулой 
, рассчитайте степень диссоциации масляной кислоты в растворах разных концентраций.
2. Все величины, рассмотренные в задании, представьте в виде таблицы.
3. Сделайте вывод о зависимости степени диссоциации масляной кислоты от ее концентрации в растворе.
Задание 2.
При определении методом Ребиндера при 200° С поверхностного натяжения растворов изоамилового спирта различной концентрации было установлено, что для раствора с концентрацией (С) 0,04 моль/л пузырек воздуха через капилляр проскакивает при разнице в уровнях жидкости в коленах манометра (h) 37 мм, для раствора с концентрацией 0,06 моль/л - при 34 мм, а для воды - при 49 мм. Поверхностное натяжение для воды (
) равно 72,75·10-3 Н/м.
1. Пользуясь формулой 
, рассчитайте поверхностное натяжение растворов изоамилового спирта разных концентраций.
2. Все величины, рассмотренные в задании, представьте в виде таблицы.
3. Сделайте вывод о зависимости поверхностного натяжения концентрации изоамилового спирта в растворе.
Задание 3.
Построить график зависимости показателя преломления водных растворов глицерина от состава по следующим данным:
| w, % | ||||||
| n | 1,333 | 1,359 | 1,378 | 1,410 | 1,427 | 1,455 |
Определить по графику, используя прием интерполяции, состав водного раствора глицерина, если показатель преломления этого раствора nх = 1,384.
Задание 4.
Построить график зависимости поверхностного натяжения водных растворов изоамилового спирта от концентрации спирта в растворе по следующим данным:
| С, моль/л |  , Н/м
|
| 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09 0,10 | 66,9 62,2 59,1 56,4 54,6 52,3 48,9 47,6 45,8 44,4 |
= 72,8 10-3 Н/м.
Сделать вывод о характере изменения поверхностного натяжения водных растворов изоамилового спирта от его концентрации в растворе.
Задание для самостоятельной работы по теме:
quot;СПОСОБЫ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНОГО МАТЕРИАЛА".
Конечная цель задания:
I. Научиться при построении графиков выбирать масштаб при откладывании по осям координат заданных величин с учетом требований, предъявляемых к выбору масштаба.
II. Научиться проводить линию графика по экспериментальным точкам, нанесенным на поле графика.
III. Научиться анализировать характер графической зависимости и пользоваться приемом интерполяции.
Задание 1.
Построить график зависимости удельного сопротивления (r) растворов вещества А от концентрации (С) (табл. 1).
I. Охарактеризовать изменение удельного сопротивления раствора при изменении концентрации электролита А в растворе.
II. Определить удельное сопротивление раствора А с концентрацией С = 0,03 кмоль/м3.
Таблица 1.
| № п/п | С, кмоль | r, Ом м | ||||||||||
| —--- м3 | ||||||||||||
| HCl | HJ | HNO3 | HJO3 | NaBrO3 | KCNS | KBrO3 | CH3COONa | CH3COOK | ||||
| 1. 2. 3. 4. 5. 6. 7. | 0,1 0,05 0,02 0,01 0,005 0,002 0,001 | 0,256 0,501 1,230 2,43 4,82 11,9 23,7 | 0,254 0,500 1,220 2,430 4,820 12,10 23,80 | 0,261 0,514 1,245 2,470 4,900 12,10 24,2 | 0,360 0,645 1,455 2,78 5,310 13,20 26,0 | 1,17 2,21 5,24 10,20 21,0 48,60 95,20 | 0,832 1,60 3,81 7,46 14,50 36,0 71,4 | 0,982 1,780 4,240 8,250 16,3 40,0 79,2 | 1,37 2,60 6,18 12,0 23,4 57,0 113,0 | 1,035 1,970 4,730 9,220 18,20 44,5 87,6 | ||
Задание 2.
Построить график зависимости эквивалентной электропроводности (l) растворов вещества А от разведения (V)(табл. 2).
I. Охарактеризовать изменение эквивалентной электропроводности раствора при изменении величины разведения раствора вещества А.
II. Определить эквивалентную электропроводность раствора А с разведением V = 300 м3/кмоль.
Таблица 2.
| № п/п | V, | l, Ом-1 кмоль-1 м2 | ||||||||
| м3 — | ||||||||||
| кмоль | HCl | HJ | HNO3 | HJO3 | NaBrO3 | KCNS | KBrO3 | CH3COONa | CH3COOK | |
| 1. 2. 3. 4. 5. 6. 7. | 10 20 50 100 200 500 1000 | 39,06 39,92 40,65 41,15 41,49 42,02 42,19 | 39,34 40,00 40,98 41,15 41,49 41,84 42,02 | 38,3 38,9 40,16 40,49 40,82 41,32 41,32 | 27,78 31,01 34,36 35,97 37,66 37,88 38,46 | 8,55 9,05 9,54 9,80 9,98 10,29 10,50 | 12,02 12,50 13,12 13,40 13,79 13,89 14.01 | 10,18 11,24 11,79 12,12 12,27 12,50 12,63 | 7,30 7,69 8,09 8,33 8,54 8,77 8,84 | 9,66 10,15 10,57 10,85 10,99 11,24 11,42 |
VII. ПЛАН РАБОТЫ НА ПРЕДСТОЯЩЕМ ЗАНЯТИИ:
1. Знакомство с правилами работы в химической лаборатории. Инструктаж по технике безопасности.
2. Тестовый контроль знаний по смежным темам курсов общей химии, физики и математики.
3. Изучение основных задач и методов физической химии. Ознакомление с особенностями проведения практических занятий по изучаемой дисциплине и подготовки к ним.
4. Изучение способов обработки экспериментального материала.
5. Выполнение индивидуальных заданий по построению графиков с последующим анализом выполненной работы.
Приложение
РЕКОМЕНДАЦИИ ПО СПОСОБАМ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНОГО
МАТЕРИАЛА.
Выполнение лабораторных работ по физической и коллоидной химии направлено на решение различных задач, в том числе:
- проверку и практическое обоснование некоторых теоретических положений;
- выяснение особенностей в поведении и свойствах систем, их природы на основе определения зависимости между параметрами, характеризующими системы.;
- приобретение навыка в практическом измерении величин, характеризующих системы.;
- усвоение теоретических основ физико-химических методов исследования;
- приобретение умения определять искомые в методе величины на основе непосредственно измеренных в опыте величин и использования соответствующих уравнений и графиков.
1. ПРАВИЛА ПОСТРОЕНИЯ ТАБЛИЦ.
При оформлении лабораторных работ таблицы могут быть использованы для систематизации экспериментально полученных и расчетных величин или для установления характера зависимости между соответствующими параметрами, характеризующими изучаемые системы, процессы.
При составлении таблиц следует придерживаться следующих правил:
а. Таблица должна состоять из строк и столбцов, расположенных в определенной последовательности: в первом столбце (или строке) записываются заданные величины, во втором и последующих экспериментально полученные, табличные и расчетные.
б. Каждый столбец (или строка) должен быть подписан с указанием величины и единиц измерения.
в. Если цифры, записанные в таблице, представлены как произведение двух величин, одна из которых число 10n,то этот общий сомножитель выносят в обозначение столбца, и если его записывают как произведение к буквенному обозначению величины, то знак в показателе степени изменяют на противоположный.
Например, поверхностное натяжение для трех растворов ПАВ различной концентрации равно σ1 = 49,2 · 10-3 Н/м; σ2 = 34,87 · 10-3 Н/м; σ3 = 30,5 · 10-3 Н/м.
Эти данные в таблицу можно записать так:
| № п/п | σ·103, Н/м |
| 49,2 | |
| 34,87 | |
| 30,5 |
г. цифры, соответствующие заданным данным в столбце, следует записывать либо в порядке возрастания величины, либо в порядке убывания.
д. при записи чисел в столбце следует каждый разряд цифр записывать один под другим: десятки под десятками, единицы под единицами, десятые доли под десятыми и т. д.
Закрепить правила построения таблиц можно, выполнив задания 1 и 2.
2. ОСНОВНЫЕ НАЗНАЧЕНИЯ ГРАФИКОВ.
При обработке результатов физико-химических измерений широко пользуются графиками. Они позволяют более наглядно, чем таблицы представить взаимные связи между изучаемыми величинами и осуществлять ряд вычислительных операций, в том числе интерполяцию, экстраполяцию, дифференцирование. Графики облегчают сравнение величин, позволяют обнаружить точки перегиба, максимума или минимума, наибольшие и наименьшие скорости изменения величин и другие особенности, которые недостаточно проявляются в таблицах. Метод физико-химического анализа основан на построении диаграмм свойство-состав с последующим их анализом. При помощи графиков не только можно установить характер зависимости между измеряемыми величинами, но и установить ее математическое выражение.
Рассмотрим некоторые примеры использования графиков.
1) Определение свойств веществ (систем) на основе характера зависимости между исследуемыми величинами.
Примеры:
1. Если с повышением концентрации вещества в растворе поверхностное натяжение уменьшается, вещество является поверхностно-активным (а). Если же с увеличением концентрации поверхностное натяжение раствора возрастает (б), то вещество является поверхностно-инактивным.
Рис.1
2. Если диаграмма плавкости соответствует рисунку "а", вещества А и В в твердом состоянии не растворяются друг в друге, а сплав представляет механическую смесь кристаллов веществ А и В, если же диаграмма плавкости имеет вид "б" вещества А и В в твердом состоянии растворяются друг в друге, образуя твердый раствор.
| 
|
Рис 2. а) б)
2) Количественное определение содержания вещества в смеси на основе калибровочной кривой.
Если установить графическую зависимость между показателем преломления раствора и составом раствора, то по показателю преломления раствора nx неизвестного состава x можно определить содержание растворенного вещества в растворе. Этот прием называется интерполяцией.
3) Определение констант в уравнении.
Зависимость между изучаемыми величинами графически может представлять собой прямую или получает такой вид после преобразования уравнения, математически описывающего эту зависимость. Построив соответствующий график, можно определить константы в уравнении.
Пример. Уравнение Фрейндлиха имеет вид: Г= 
= K C1/n, где "К" и "1/n" - константы. Данное уравнение соответствует уравнению вида y = a хb. График зависимости Г = f(C) или (y = f(x)) представляет параболу. После преобразования уравнения логарифмированием оно принимает вид: lgГ = lgK + 1/n lgC, что соответствует уравнению вида: y = a + bx.
Если построить график, отложив по оси "Х" величины lgC, а по оси "У" величины lgГ, то график должен представлять прямую, не проходящую через начало координат, а отсекающую (при продолжении линии графика) на оси "У" отрезок, соответствующий значению lgК. Тангенс угла наклона этой прямой к оси lgС будет соответствовать величине 1/n.
ОА = lgК
tg 
4) Экстраполяция.
Графическая экстраполяция производится посредством продолжения линии графика за пределы опытных данных. Она достаточно надежна, если изучаемая зависимость выполняется и вне области производимых измерений. Примером экстраполяции может быть рассмотренный в пункте 3 способ нахождения значения отрезка АО, соответствующего lgК.
5)Графическое дифференцирование.
В основе графического дифференцирования лежит закономерность:
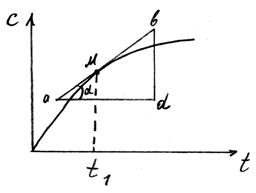где 
- угол, образуемый с положительным направлением оси Х касательной, проведенной к кривой y = f(x) через точку М, абсцисса которой соответствует заданному значению "Х".
3. ПРАВИЛА ПОСТРОЕНИЯ ГРАФИКОВ
При построении графиков необходимо провести оси координат, обозначить величины, откладываемые по осям, и единицы их измерения.
А) ПРАВИЛА ВЫБОРА МАСШТАБА ПРИ ПОСТРОЕНИИ ГРАФИКОВ.
1) Разделить оси координат на равные отрезки, каждый из которых обозначить в соответствии с выбранным масштабом. Длина отрезков и их значения по осям "Х" и "У" могут не совпадать.
2) Масштаб выбрать таким, чтобы легко можно было отложить данную величину или прочитать искомую с заданной точностью. Цена деления (например, 1 клеточка на миллиметровой бумаге) масштаба должна соответствовать точности откладываемой величины. Например, если по оси "Х" откладываем числа: 1,25; 2,38; 4,32 и т.д., то при выборе масштаба по оси "Х" следует одно деление принять равным 0,01, но не 0,1 или 1.
3) Цена деления по осям "Х" и "У" может не совпадать.
4) Масштаб должен быть таким, чтобы график занимал все поле между осями координат, а линия графика шла под углом 45о. Метод интерполяции в этом случае дает наибольшую точность.
5) Чтобы график занимал все поле чертежа, иногда величины следует откладывать не от "0".
Б) ПРОВЕДЕНИЕ ЛИНИИ ГРАФИКА ПО ЭКСПЕРИМЕНТАЛЬНЫМ ТОЧКАМ.
1) Линия графика не должна быть ломаной (если это не имеет место из теоретических соображений).
2) При проведении линии не обязательно, чтобы все точки легли на нее. Линию следует провести так, чтобы число точек, которые на нее не легли, и расстояние их от кривой по одну сторону равнялись числу точек и расстоянию их от кривой по другую сторону.
3) Линию графика следует проводить тонкой, но хорошо видимой.
В) РЕКОМЕНДАЦИИ К ОФОРМЛЕНИЮ ГРАФИКА.
1) Все графики выполняются на миллиметровой бумаге размером в страницу листа лабораторного журнала.
2) Оси координат и линию графика рекомендуется проводить карандашом. Обозначения осей координат, масштабных отрезков и точек на поле графика - чернилами.
3) Если график построен для нахождения каких-то величин, то на графике следует провести соответствующие пунктирные линии.
4) На листе, где выполнен график, должны быть указаны номер или тема работы и название графика.
5) При проведении графиков можно пользоваться правилом предварительного округления более точных данных: если некоторые данные имеют больше десятичных знаков или больше значащих цифр, чем другие, то их предварительно следует округлить, сохраняя лишь одну лишнюю цифру.
Закрепить правила построения графиков можно, выполнив задания 3 и 4.
4. ПРАВИЛА ОКРУГЛЕНИЯ ЧИСЕЛ.
Округлением числа называют уменьшение количества цифр в числе путем отбрасывания одной или нескольких последних цифр.
Можно пользоваться следующими правилами округления:
1) Если первая отброшенная цифра меньше 5, то последнюю из сохраняемых цифр оставляют без изменения.
2) Если первая отброшенная цифра равна 5 или больше 5, то последнюю сохраняемую увеличивают на единицу.
3) При округлении целых чисел отброшенные цифры заменяют нулями.
4) Как правило, округленные целые числа записывают как произведение двух сомножителей, один из которых представляет число 10n.
Например, числа 264213, 264000 можно представить как 2,64 · 105.
5. ПОГРЕШНОСТИ ИЗМЕРЕНИЙ.
Измерения с помощью приборов и различные аналитические операции неизбежно сопровождаются погрешностями. Источники погрешностей многочисленны и разнообразны. Различают погрешности систематические и случайные.
Систематические погрешности обусловлены постоянно действующими факторами и не изменяются по величине и знаку при повторных опытах. Они возникают при измерениях на неправильно установленных приборах, при использовании неточно откалиброванной посуды, при титровании раствором с неправильно установленным титром и др. Систематические погрешности трудно заметить, так как при параллельных измерениях получаются совпадающие результаты. Убедиться в отсутствии систематических погрешностей можно только путем проведения измерений другим методом. Если обнаружены систематические погрешности, то вводят соответствующие поправки. Систематические погрешности характеризуют правильность метода (разность между средним результатом измерений и истинным значением).
Случайные погрешности обусловлены причинами случайного характера: изменением температуры, давления, влажности воздуха. Они легко выявляются при параллельных измерениях, но трудно оцениваются, так как изменяются от опыта к опыту по величине и знаку. Случайные погрешности характеризуют точность метода (воспроизводимость полученных результатов).
В большинстве случаев имеют место небольшие случайные погрешности, поэтому результаты параллельных измерений достаточно близки между собой.
Большие случайные погрешности называют промахами. Они возникают при невнимательности экспериментатора, при неправильной подготовке опытов, из-за ошибок в вычислениях. Промахи случаются редко, поэтому соответствующие результаты отбрасывают.
Случайные погрешности по способу выражения делят на абсолютные и относительные.
Абсолютная погрешность (Δ) представляет собой разность между истинным значением величины Хист и найденным значением Xэксп, поэтому она имеет размерность измеряемых величин:
Δ = Хист - Xэксп (1)
Отношение абсолютной погрешности к полученному значению X называют относительной погрешностью. Ее обычно выражают в процентах:
(2)
Относительная погрешность дает представление о качестве измерения.
Экспериментатора всегда интересует истинная величина. Однако определение ее невозможно, так как в уравнении (1) неизвестна величина Δ. По этой причине с помощью статистической теории погрешностей находят наиболее вероятное значение определяемой величины и указывают возможные отклонения от него.
Измерения могут быть прямые и косвенные.
