Медицинаның түрлі саласында құбылыстардың немесе белгілердің бір бірімен байланысын статистикалық талдаудан өткізуге тура келеді. Сонымен қатар факторлы және нәтижелі белгілердің арасындағы байланысты да анықтау қажет.
Бұл әдіс әр адамның дене өсуін бағалауда пайдаланылады және әр адамнын функционалды көрсеткіштерге түрлі сыртқы факторлардын әсерін ғылыми түрде дәлелдеу үшін керек.
Өзара байланыс екі түрге бөлінеді:
1. Функциоиалдық.
2. Корреляциялық.
Функционалдык байланыс – белгілердің бір-бірімен өзара қатынасын көрсетеді. Бұл белгілердің әрқайсысының мөлшеріне басқа белгілер мөлшерінің нақты сәйкес келуі талап етіледі. Мысалы, шеңбердің радиусы үлкейген сайын оның көлемі де үлкейеді: суда тұздық мөлшері көбейсе оның ащылығы да көбейеді. Негізгі функиионалды байланыс - физикалық, химиияық құбылыстарға тән.
Корреляциялық байланыс - бір белгінің әрбір орта мөлшерінін мағынасы басқа бір белгімен өзара байланысу арқылы бірнеше мағынаға сәйкес келеді (нәрестенің бойы мен салмағының арасындағы өзара байланыс. әйелдердің бала туу жиілігі мен отбасының табысы арасындағы өзара байланыс, т.б.). Көбінесе, корреляциялық байланыс әлеуметтік-мединалық, биологиялық, медицинадық өзгерістерге тән. Сонымен қатар корреляциялық байланыстың ерекшелігі – ол тек бақылау санын есептегенде, яғни статистикалық жинақты зерттегенде анықталады. Корреляция коэффициентінің мөлшеріне сәйкес (0-ден 1-ге дейін) белгілер арасындағы байланыстың күші мен бағытын білуге болады.
Корреляциялық байланыс бағыты бойынша: тікелей, кері болып 2-ге бөлінеді.
Корреляциялық байланыстың күшін анықтау нұсқасы:
1. Күшті ±1,0 ден ±0,7 дейін;
2. Орташа ±0,7 ден ±0,3 дейін;
3. Әлсіз ±0,3 тен ±0,1 дейін;
4. Жоқ - 0.
Егер (+) болсатікелей байланыс дейміз.
Егер (-) болса, оны кері байланыс дейміз.
Корреляциялық байланыстар: кестелік, графикалық, корреляциялықкоэффициентер арқылы бейнеленеді.
Корреляциялық коэффициент есептеудің екі тәсілі бар. Олар:
1. Квадратты тәсіл (Пирсон тәсілі).
2. Рангілі (сандық, реттеу) тәсіл (Спирмен тәсілі).
Квадратты тәсілді қолданудың жолдары мыналар:
1. егер белгілер сан жағынан көп болса;
2. егер белгілер арасында байланыс күшін нақты түрде анықтау қажет болса.
Пирсонның тәсілі бойынша корреляциялық коэффициентті есептеу формуласы былайша белгіленеді:
(46)
мұндағы, 
- корреляциялық коэффициент, «х» және «у» өзара байланысын анықтайын белгілер, dx және dy әрбір ауыспалы вариантаның, өзінің орта арифметикалық өлшемінен ауытқуы (Мх және Му).
Пирсон тәсілі бойынша корреляциялық коэффициентті есептеу әдісі мен тәртібі:
1. ауыспалы («х» және «у») белгілерден вариациялы қатар құру;
2. әрбір вариациялы қатардың орта өлшемін анықтау;
3. «х» және «у» қатары үшін орта өлшеміне әр вариантаның (dх және dу) ауытқуын табу;
4. ауытқулардың көбейтілгеннен (dх•dу) кейінгі қосындысын табу керек (∑(d 
x•dу));
5. әрбір ауытқуды квадратқа алып және қатар бойынша қосындысын табу керек (
);
6. көбейтіндісін тауып шығару керек (
);
7. корреляция коэффициентінің формуласына шыққан нәтижелерін қоңдырып есептеу керек:
(47)
Есептелген нәтиже 0 мен 1,0 арасында (+) немесе (-) белгімен болуы мүмкін. Ол байланыстың бағыты мен күшін көрсетеді.
Рангтық корреляция тәсілін қолдану жөніндегі нұсқаулар:
1. Егер байланыс күшінің деңгейін нақты түрде білу қажет болмаса, ондай мәліметтерді болжамдап алуга болады.
2. Егер белгілер (n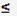 
30) сан жағынан және сапалық белгілер болса, (атбутивті белгі) деп аталады.
3. Рангілі тәсілі бойынша корреляциялық коэффициента есептеу формуласы:
(48)
мұндағы, 
- рангілі корреляция коэффициенті, d - рангтардың айырмашылығының ауытқуы, п - бақылау саны.
Рангілі корреляция коэффициентін есептеу жолы:
1. Салыстырылатын белгілерден қатар құру, қатарды «х» және « у» деп белгілейміз. Бірінші қатардың «х» белгісін өсу немесе төмендеу бойынша реттік санмен белгілеу (1,2,3,4...), екінші қатардың (у) мағынасын бірінші қатардағы мағынасына сәйкес келетіндей қарсысына қою керек.
2. Әрбір белгінің өлшемін рангілі номермен (реттік санмен) белгілеу керек, оны «х» жене «у» дейміз. Рангілі қатарда белгінің бірдей мөлшері болса, осы мөлшердің реттік нөмерлерінің косындысының орташа саны деп алуға болады.
3. «х» және «у» арасындағы рангтердің айырмашылығын анықтау d=xi-yi;
4. Әрбір рангының айырмасын квадратқа алу (d2).
5. Рангінің айырмасының квадраттарының қосындысын табу (∑ d2).
Табылған нәтижелерді формулаға қондырып есептеу керек.
Корреляция коэффициентінің қатесін есептеу формуласы:
1. Пирсон тәсілі бойынша есептелген корреляция коэффициентінің қатесін мынадай формуламен табады:
(49)
2. Спирмен тәсілі бойынша рангтік корреляция коэффициентінің қатесін мынадай формуламен табады:
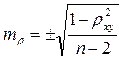(50)
Квадратты тәсілмен есептелген корреляция коэффициентінің дұрыстық критерийін анықтайтын формула:
(51)
Рангілі корреляция коэффициентінің дұрыстық критерийін анықтайтын формула:
(52)
Есептелген коэффициенттердің сенімді болуы дұрыстық (t)критерийімен анықталады. Коэффициентті сенімді деу үшін дұрыстық критерийі t «2»-ге тең, не одан жоғары болуы керек.
Тақырып бойынша бақылау сұрақтары:
1. Процестер мен құбылыстар арасындағы байланыстың түрлері.
2. Функционалдықбайланысқа анықтама.
3. Корреляциялық байланысқа анықтама.
4. Функционалдық және корреляциялық байланыстың арасындағы айырмашылық.
5. Корреляциялық байланысты көрсетудің тәсілі.
6. Корреляциялық коэффициент анықтайтын тәсілдер.
9. Пирсон тәсілі бойынша корреляциялық коэффициенттің формуласы мен есептеу жолы.
10. Спирмен тәсілін қолдану (рангілі, ретті корреляция).
11. Спирмен тәсілі бойынша корреляциялы коэффициенттің қатесін, сенімділігін есептеу формулалары.
12. Дәрігерлердің жұмысында корреляциялы коэффициент әдісін пайдалану.
11. Сызықтық регрессия
Екі айнымалы шаманың бір-бірімен байланысының бағыты мен күші корреляциялық көрсеткіші арқылы анықталады, ал бір белгі мөлшерінің екінші белгінің мөлшері өзгергенде сан жағынан қаншалықты өзгеретіні регрессия тәсілі арқылы көрсетіледі.
Регрессия – бір-бірімен байланысты белгілердің бірінің шамасы белгілі болса, екіншісінің орта шамасын табуға мүмкіншілік беретін тәсіл.
Регрессия коэффициенті Rу/x - абсолюттік шама, ол бір белгінің мөлшері бірлік санға өзгергенде екінші белгінің олшемі каншалықты өзгеретінін көрсетеді.
Регрессия коэффициентін есептеу формуласы:
(53)
мұндағы, Rу/x- регресcия коэфффициеті, rxy- корреляция коэффициенті, 5 және 5у (X және Ү қатарларының орта квадратты ауытқуы). Мысал: 9 жасар қыздардың орта шамамен бойларының ұзындығы белгілі, ал осы жастағы қыздардың бойы 1 сантиметрге өскенде орта ессппен салмағы қанша килограммға ұлғаятынын білуге болады. “Ү” арқылы олардың салмағы мен “X” арқылы бойларын белгілейміз. Бойларының орта квадратты ауытқуы да белгілі, ол δХ=±5,8. Салмақтарының орта квадратты ауытқуы да белгілі, ол δ = ±4,2 бойы мен салмақтың корреляциялық көрсеткіші rху = +0,6 бұл мәліметтер бұрынғы зерттеулерден алынады. Сонда регрессия коэффициенті мынадай болады:
Қорытынды: 9 жасар қыздардың орта шамамен бойы 1 см өскенде салмағы орта есеппен 0,43 килограммға көбейеді.
Регрессия коэффициенті арқылы бір белгінің (мысалы салмақтың) мөлшерінің арнайы олшеу жүргізбей-ақ, екінші белгінің (мысалы, бойдың) орта шамасы бойынша табуға болады. Ол үшін сызықтық регрессия теңдеуін пайдаланады:
Y=My+Ry/x (X-Mx)(54)
мұндағы, Y - ізделіп отырған (салмақтың) шамасы, X - белгілі (бойдың) шамасы. R y/x - салмақты бойға салыстырғандағы регрессия коэффициенті.
М - белгілі жасқа тән (салмақтың) орта шамасы.
М - бойдың орта шамасы.
Мысал: 9 жасар қыздардың орта есеппен салмағы Му=30,3 кг, бойының шамасы М=135,5 см. Егер де 9 жасар қыздардың орта есеппен бойының ұзындығы 132 см болса, онда салмағының орта шамасы қанша болатынын табуға болады. Барлық белгілі мәліметтерді регрессия теңдеуіне жазамыз:
Ү =30,3+0,43 (132-135,5) = 28,8 кг.
Қорытынды: Орта есеппен 9 жасар қыздардың бойының ұзындығы 132 см болса, бұған сәйкес салмақтын мөлшері орта шамамен 28,8 кг болады.
Жеке адамдардың белгілерінің мөлшері әртүрлі. Мысалы, бойларының ұзындығы бірдей болғанымен, салмағына тән өзгерушіліктің шамасын табу үшін регрессия коэффициентінің ауытқуы 
қолданылады:
(55)
мұндағы, 
- зерттелінетін белгінің (мысалы, салмақтың) орта квадратты ауытқуы, rxy- корреляция көрсеткіші.
Неғұрлым -тың мөлшері аз болса, соғурлым әр аламның зерттелген белгісінің орта шамасынан айырмашылығы аз болады.
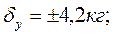
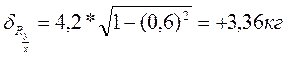
Регрессия теңдеуін және регрессия ауытқуын пайдаланып регрессия коэффициенті аркылы регрессия шкаласын құрады. Бұл шкала бойынша балалардың және жасөспірімдердің дене дамуын зерттегенде бойдың, салмақтың, кеуде көлемінің мөлшерлерінің жасына сәйкестігін бағалайды.
Регрессия шкаласы бойынша қан қысымының ең жоғарғы деңгейі белгілі болса, оған сәйкес ең төменгі деңгейін табуға болады, ал жұқпалы аурумен ауырғандардың саны белгілі болса, шкала бойынша бацилла сақтаушылардың санын анықтауға болады. Осы принципті қолданып әр түрлі есепте қолданылатын геометриялық шаманың графигі жасалады. Номограмма арнайы тор сызық секілді болады. Онда бір сызықта бір белгінің мөлшерлері жазылса, екінші сызықта соған сәйкес екінші белгінің шамасы жазылады. Бұл регрессиялық әдіс жұмыстар жүргізілгенде де және дәрігерлердің (бала дәрігерлері, эпидемиологтар, санитарлық дәрігерлер) күнделікті жұмысында да қолданылады.
Тақырып бойынша бақылау сұрақтары:
1. Регрессия тәсілінің анықтамасы қандай?
2. Регрессия талдауы медицинада қалай пайдаланылады?
3. Регрессия коэффициенті қандай формуламен есептелінеді?
4. Регрессия ауытқуының маңызы?
5. Регрессия тәсілінің маңызы?
