Евклид (б.э. дейінгі 330 - 275 жылдар) – Платон мектебінің тәрбиесін алған ғалым, кейін александрияда математикадан сабақ берген. Оның «Негіздемелерінде» геометрияның негізгі арнасы жүйелі түрде баяндалған, бұл еңбектің зор шеберлікпен жазылғандығы сонша, геометрия ғасырлар бойы осы шығарма бойынша оқытылып келген.
Евклидтің «Негіздемелері» 13 кітаптан (яғни тараудан) құралады.
1- кітап. Үшбұрыштар туралы теоремалар, параллель түзулердің теориясы, үшбұрыштар мен көпбұрыштардың тең шамалы болу шарттары, Пифагор теоремасы.
2- кітап. Көпбұрышты оған тең шамалы болатын квадратқа айналдыру.
3- кітап. Шеңбер.
4- кітап. Іштей және сыртттай сызылған көпбұрыштар, дұрыс n- бұрышты салу жолдары (n=5,6,10, ал n=3 жағдай 1-кітапты қарастырылған болатын).
5- кітап. Пропорциялар теориясы.
6- кітап. Көпбұрыштардың үұсастығы.
7, 8, 9- кітап. Геометриялық жолмен баяндалған арифметика.
10- кітап. Ортақ өлшемі жоқ шамалар.
11, 12, 13- кітап. Бұларда стереометрияның негіздемелері баяндалған, ал 13- кітап түгелімен дұрыс көпжақтар жөніндегі ілімге арналған.
Геометрияның Евклидтің тұсында ғалымдарға мәлім болған бірталай материалы «Негіздерде» айтылмаған.
Постулаттар. I. Кез келген нүктеден басқа бір кез келген нүктеге дейін түзу сызық жүргізуге болатындығы талап етіледі.
II. Әрбір (шектеулі) түзуді қажетінше соза беруге болатындығы талап етіледі.
III. Кез келген центрден кез келген радиуспен шеңбер сызуға болатындығы талап етіледі.
IV. Тік бұрыштардың бәрінің бірдей болуы талап етіледі.
V. Әрдайым екі түзуді үшінші бір түзу қиып өткенде үшінші түзудің бір жағында қосындысы екі тік бұрыштың қосындысынан кем ішкі тұтас бұрыштар құралатын болса, шектеусіз созғанда алғашқы айтылған екі түзудің қиылысатындығы және қосындының екі тік бұрыштың қосындысынан кем жағында қиылысатындығы талап етіледі.
Аксиомалар. І. Әрқайсысы өз алдына үшінші бір шамаға тең екі шама біріне бірі тең болады..
ІІ. Тең шамаларға тең шамаларды қосқанда шығатын қосындылар да тең болады.
VII. Бірінің орнына екіншісі дәл келетін фигуралар біріне бірі тең болады.
Содан кейін Евклид геометрияның теоремаларын баяндайды, бұл теоремалардың әрқайсысы бұрын қарастырылған теоремаларды, постулаттарды және аксиомаларды ғана пайдаланып дәлелдеуге боларлықтай етіліп, реттелген жүйе бойынша орналастырылады.
Теорема. Әрбір А∉ а нүктесі арқылы а түзуіне параллель болатын бір ғана түзу өтеді.
Теорема (кері теорема). Егер а түзуінен тысқары жататын әрбір а нүктесінен сол а түзуіне параллель болатын бір ғана түзу өтетін болса, онда V постулат дұрыс болады (оны теорема ретінде дәлелдеуге болады).
Тік бұрыштың шамасын d әрпімен белгілейік. Жазық бұрыш екі тік бұрыштың қосындысындай болады, сондықтан b шамасы 2d-ге тең болады.a түзуі мен А∉а нүктесі берілсін, А нүктесі арқылы екі түзу, атап айтқанда, а түзуін В нүктесінде қиып өтетін с түзуі мен
(1)
теңсіздігін қанағаттандыратын b түзуі өтсін (2 - сурет). b түзуі а түзуін қиып өтетіндігін жіне олардың b∩а қиылысу нүктесі с нүктесімен шектелген, 
бұрыштары орналасқан, П жарты жазықтығында жататындығын дәлелдеу керек.
болатындай етіп,бір а´∋А түзуін жүргізейік. Сонда
(1), (2) 
(3)
Болатындықтан, (2), (3)⇒ 
шығады. Бұдан а´ ⃦ а болатындығы көрінеді (ал а´түзуі а түзуін қиып өтеді деу тағы да үшбұрыштың сыртқы бұрышы туралы теоремаға қайшы қорытындыға келтірер еді, сыртқы бұрышы туралы теореманың дәлелдемесінде V постулат пайдаланылмайды). Біз айтылып отырған параллель түзудің біреу ғана болатындығын постулат ретінде қабылдадық. Сондықтан b түзуі а түзуін (b≠a´) қиып өтеді. Енді b∩a ∊ П болатындығын дәлелдеу ғана қалды. 
және 
болғандықтан, 
болады. Сондықтан а және b түзулері с түзуімен шектелген, бірақ 
мен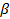 
бұрыштарын қамтымайтын П´ жарты жазықтығында қиылыса алмайды, өйткені қиылысады деп ұйғару, тағы да үшбұрыштың сыртқы бұрышы туралы теоремаға қайшы қорытындыға келеміз, олай болса, а және b түзулерін П жарты жазықтығында қиылысады.
Сонымен, V постулат мынадай ұйғарымға эквивалент (парапар) болады: А∉а нүктесінен өтіп, берілген а түзуіне параллель болатын бір ғана түзу болады.
Одан әрі екі параллель түзуді үшінші бір түзу қиып өткенде құралатын сәйкес бұрыштардың конгруэнт болатындығы, үшбұрыштың ішкі бұрыштарының қосындысы 2d-ге тең болатындығы т.б. теоремалар дәлелденеді. Демек, V постулат геометрияның маңызды теоремаларының көпшілігінің негізінде жатыр.
НЕГІЗГІ ӘДЕБИЕТТЕР.
1. Александров А. Д., Нецветаев Н. Ю. Геометрия: Учеб. пособие.— М.; Наука. Гл. ред. физ.-мат. лит., 1990.— 672 с:
2. Атанасян Л.С, Базылев В.Т. Геометрия. В 2-х ч. Ч. I. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов.— М.: Просвещение, 1986.— 336 с
3. Атанасян Л.С, Базылев В.Т. Геометрия. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов. В 2 ч. Ч. 2.— М.: Просвещение, 1987.—352 с:
ҚОСЫМША ӘДЕБИЕТТЕР
1. Ефимов Н.В. Высшая геометрия. — 7-е изд. — М.: ФИЗМАТЛИТ, 2004. - 584 с.
2. Егоров И.П. Основания геометрии. М., Просвещение 1984г7
3. Кузютин В.Ф., Зенкевич Н.А., Еремеев В.В. Геометрия: учебник для вузов. - Лань, 2003. - 415 c.
4. Прасолов В. В., Тихомиров В.М. Геометрия.—М.: МЦНМО, 2007.—2-е изд., перераб. и доп.—328 с:
