Жоспары:
- Планиметрияның кейбір теоремаларын дәлелдеу
- Стереометрия теоремаларын дәлелдеу мысалдары
Дәріс тезисі
Планиметрияның кейбір теоремаларын дәлелдеу
Біз бұл параграфта тек бір П жазықтығында раналасқан фигураларды ғана қарастырамыз.
Естеріңізге сала кетейік, жазықтықтың қозғалысы(немесе орын ауыстыруы) деп біз оның кез келген екі нүктесінің арасындағы қашықтықты сақтайтын түрлендіруін айтамыз. Егер бізге ортонормаланған репер 
берілсе, онда R реперін R/ реперіне аударатын бір ғана қозғалыс болады, онда ол нүкте осы қозғалыстың нәтижесінде R/ реперінің М/ нүктесіне көшеді, бұл нүктенің координаталары да сол x,y болады. Қозғалыс үш нүктенің қатынасын өзгертпейді, демек, түзуді түзуге, кесіндіні кесіндіге, сәулені сәулеге, жарты жазықтықты жарты жазықтыққа аударады.
F1 мен F2 фигураларының бірін екіншісіне аударатын қозғалыс болса, бұл фигуралар конгурент немесе бірінің орныныа екіншісі сай келетін) фигуралар деп аталады.
Қозғалыстар группа құрастырғандықтан, фигуралардың конгуренттік қасиеті барлық фигуралар жиыны үстіндегі эквиваленттік қатынас болып табылады.
1- теорема Жазықтықта [ОХ) және [О/ Х/) сәулелері, (ОХ) түзуімен шектелген П0 жарты жазықтығы, (ОХ) түзуімен шектелген П0 жарты жазықтығы берілсін. Онда жазықтықтың [ОХ) сәулесін [О/ Х/) сәулесіне П0 жарты жазықтығына аударатын бір ғана қозғалысы болады.
Мынадай ортонормаль реперлерді қарастырайық (142- сурет)
R реперін R/ реперіне аударатын f қозғалысы [ОХ) сәулесін [О/ Х/) сәулесіне П0 жарты жазықтығын П0 жазықтығына аударады.
2- теорема (кесінділерді өлшеп салу туралы). Жазықтықта[ОХ) сәулесі мен [АВ) кесіндісі берілсін. Онда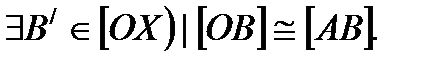 
Мұндай В/ нүктесі біреу ғана болады.
Мынадай ортонормаль реперлерді қарастырайық (143 – сурет)
R реперін R/ реперіне аударатын f қозғалысы болады.
3- теорема. 
[AB] 
[A /B/],болғандықтан f|f ([AB])= [A /B/] қозғалысы болады (144- сурет) f қозғалысы А нүктесі жатпайтын [BС] сәулесін f(А)=A/ нүктесі жатпайтын В/ нүктесінен басталатын сәулесіне аударады. Сондықтан|f ([BС])= [В /С/) ал шарт бойынша [BС]
[В /С/] онда 2 теореманың салдары бойынша:
2. Бізге [AB] және[СD] екі кесінді берілсін. Кез келген [ОХ) және[OВ/] [AB] және [OD/] [СD] кесінділерін салайық. (145- сурет).
Сонда төмендегідей жағдайлардың болуы мүмкін:
1) 
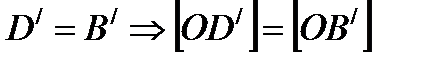. Ал [AB] және [СD] кесінділері [OВ/] кесіндісіне когурентті, сондықтан [AB] [СD]
2) 
. Онда [AB] кесіндісі [СD] кесіндісінен үлкен, ал [СD] кесіндісі [AB] кесіндісінен кіші дейді де, былай жазады:
[AB]> [СD] немесе [СD]< [AB]
4- теорема (бұрышты өлшеп салу туралы). Жазықтықта
а) (АВ) түзуімен шектелген П0 жарты жазықтығында жататын дөңес ВАС бұрышы берілсін;
б) [О/ Х/) сәулесі және (OX) түзуімен шектелген П0 жарты жазықтығы берілсін. Онда П0 жарты жазықтығында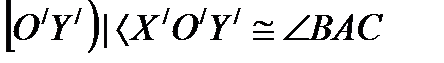 
сәулесі болады. Мұндай [О/ Ү/) сәулесі біреу ғана болады.
4 теорема бойынша 
қозғалысы болады.
ВАС дөңес бұрышы П0 мен 
жарты жазықтықтарының қилысуы болағандықтан (146- сурет), f қозғалысы ВАС бұрышын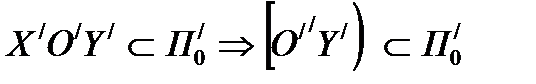 
дөңес бұрышына аударады.
5- теорема [ОС) сәулесі АОВ бұрышының қабырғаларының арасында, ал [О/ С/) сәулесі АОВ бұрышының қабырғаларының арасында жатсын. Сонда егер <АОС <А/ О /С/ және <СОВ С/ О /В болса /<АОВ <А/ О /В/ болады.(147 –сурет)
Екі дөңес бұрыш <ВАС мен <MNL, берілсін (148- сурет)
Бір [О Х) сәулесін және (ОХ) түзуімен шектелгенП0 жарты жазықтығын алаық 4- теорема бойынша П0 жарты жазықтығында мына 
шарттарын қанағатттандыратын [ОҮ) және [ОZ) сәулелері болады. Өзінің сыбайлас бұрышына конгурэнт болатын бұрыш тік бұрыш деп аталады.
6- теорема. Тік бұрыштар болады.
Мынадаай ортогональ реперлерді қарастырайық
Мұнда 
(151- сурет).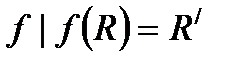 
қозғалысы бары мәлім 
дөңес бұрыштары әрі сыбайлас, әрі конгурэнт. Сондықтан бұл бұрыштардың әрқайсысы тік болады.
Вейльдің 3 –аксиомасына сай етіліп, көшірулер кеңістігінде билиниялық форма арқылы анықталған векторлардың ортогональдығы туралы ұғым евклидтік нүктелік кеңістіктегі тік бұрыш ұғыммен тығыз байланысты болып келеді.
7- теорема. <ХОҮ тік бұрыш ↔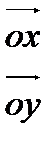 
векторлары бір біріне ортогональ.
Дөңес көпбұрыш тік бұрыштан үлкен болса, доғал бұрыш деп аталады, ал тік бұрыштан кіші болса – сүйір бұрыш деп аталады. Екі түзу а және в қилысқанда төрт бұрыш құралады, олар нөмірленіп 1,2,3,4 деп көрсетілген 153- сурет. Егер осылардың біреуі тік бұрыш болса, қалған үшеуі де тік бұрыштар болады.. Бұл жағдайда а және в түзулері тік бұрыш жасап қилысады немесе а және в түзулері өзара перпендикуляр дейді, ал олардың әрқайсысын екіншісіне түскен перпендикуляр деп атайды. Өзара перпендикуляр түзулерде жататын кесінді(сондай ақ екі сәуле кесінді мен түзу, сәуле мен түзу, кесінді мен сәуле) өзара перпендикуляр делінеді.
векторлары тік бұрыш жасап. О нүктесінде қилысатын а және в түзулерінің бағыттаушы векторлары болсын 154 сурет
8 теорема. А түзуі мен В нүктесі берілсін В нүктесі арқылы а түзуіне перпендикуляр өтеді, ол біреу ғана болады.
Салдар. Бір түзуге түсірілетін екі перпендикуляр қилыспайды (егер олар қилысатын болса, онда олардың қилысу нүктесінен берілген түзуге екі перпендикуляр жүргізілген болар еді, ол жәйіт 8 –теоремаға қайшы келер еді)
Бұдан кейін мына теоремаларды дәлелдеуге болады:
1. Тең бүйірлі үшбұрыш туралы теорема
2. Үшбұрыштардың конгурэнттігінің бірінші, екінші, үшінші белгілері
3. үшбұрыштың сыртқы бұрышы туралы теорема
4. мынадай теорема: егер әр түрлі екі түзу а және в түзулері, бір жазықтықта жатса және олар үшінші бір с түзуімен қилысқанда құралатын бұрыштар үшін төмендегі үш шарттың бірі орындалатын болса
а) сәйкес бұрыштар конгурэнт болса (<а <2)
б) ішкі бұрыштар конгурэнт болса (<1 <3)
в) ішкі тұтас бұрыштардың қосындысы (<1+<4) жазық бұрыш болса онда қалған екі шарт та орындалады және а,в түзулері қилыспайды. 155 сурет
Естеріңізге салайық Вейль аксиомалары арқылы құрылған геометрияда өздерінің бағыттаушы векторлары коллинеар болатын екі түзу, а және в түзулері параллель түзулер деп аталады. Мұндай түзулер бір жазықтықта жатады және олар қилыспайды немесе беттескен түзулер болады.. Анықтамадан мынандай салдар шығады:
1) берілген А нүктесі арқылы берілген а түзуіне параллель болып, бір ғана түзу өтеді;
2) Паралельдік дегеніміз- барлық түзулер жиыны үстіндегі эквиваленттік қатынас;
3) Егер параллель а және в түзулерінің жазықтығында жататын с түзуі алдыңғы екі түзудің бірін қиып өтетін болса, онда ол екіншісін де қиып өтеді;
4) Егер екі түзу параллель болса, онда олар кез келген қиюшы түзумен мынадай бұрыштар құрастырады(параллель түзулердің қасиеттер):
а) конгурэнт сәйкес бұрыштар құрастырады;
б) конгурэнт ішкі айқыш бұрыштар құрастырады;
в) тұтас екі бұрышының қосындысы жазық бұрыш болатын ішкі бұрыштар құрастырады
3-4 салдарлар керісінше ұйғару тәсілімен оңай дәлелденеді.
9- теорема. Үшбұрыштың ішкі бұрыштарының қосындыс жазық бұрыш болады
Кез келген АВС үшбұрышын 156 сурет алайық. А нүктесі арқылы а║(ВС) түзуін жүргізейік. Сонда <1 <В, <2 <С. Ал (<1+<2+<А)- жазық бұрыш. Сондықтан (<А+<В+<С)- қосындыс жазық бұрыш.
Салдар: Үшбұрыштардың сыртқы бұрышы өзімен сыбайлас емес екі ішкі бұрышының қосындысына конгурэнт болады.
