Жаратылыстану жәнк ақпараттандыру факультеті
Математика және физика кафедрасы
Дәріс кешені
Геометрия негіздері пәні бойынша
5В010900-Математика мамандығына арналған
Дәріс кешенінің құрылымы
Дәріс. Математикалық структура ұғымы, изоморфизм
Жоспары
1. Математикалық структура ұғымы, изоморфизм.
2. Аксиомалар системасының интерпретациялары (модельдері)
3. Структуралардың изоморфизмі
Дәріс тезисі
Қатынас ұғымын еске түсірейік. Ешқайсысы бос жиын болмайтын М1 , М2,..., Мn жиындары берілсін. Кез келген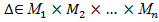 
бөлімше жиын М1, М2,..., Мn жиындарының ішінде анықталған n ар қатынас деп аталады. Егер (m1, m2,…, mn) 
болса, онда m1, m2,…, mn, мұнда (mi 
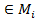) элементтері 
қатынасында дейді.
Егер 
және, сондықтан, 
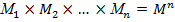болса (мұнда Мnдәрежесі – М жиынының n-ші декарттық дәрежесі), онда 
n-ар қатынасы М жиыны ішінде анықталған дейді.
бинар қатынас болған жағдайда (n=2) (m1,m2) орнына 
деп жазады. Егер 
жиыны үстінде
алгебралық операция (композицияның ішкі заңы) анықталған болса, онда оны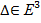 
бөлімше жиын арқылы, мұнда 
ретінде алып, Е жиынының ішінде анықталған тернар қатынас (n=3) рөлінде қарастыруға болады.
Егер Е жиынының үстінде операторларының жиыны Ʌ болатын
Композицияның сыртқы 
заңы анықталса, онда оны 
бөлімше жиыны арқылы, 
ретінде алып, Ʌ, Е жиындарының жиындарының ішінде анықталған тернар қатынас ролінде қарастыруға болады.
Егер біз 
декарттық көбейтіндіден әр түрлі екі бөлімше жиын, мысалы, ∆1 мен ∆2 бөліп шығарсақ, онда біз М1 , М2,..., Мn жиындарының системасында әр түрлі екі қатынасты анықтаймыз. ∆1 ≠ ∆2 болғандықтан, ∆1 қатынасының ∆2 қатынасынан қасиеттері бойынша өзгешелігі болмай қоймайды.
Математика өзінің алдына ондай мақсат қоймайды да. Математиктер белгілі бір мағынада мәселені керісінше қарастырады деуге болады: олар қасиеттері алдын ала берілген қатынастары болатын жиындарды іздеп тауып, соларды зерттейді.
Бос емес әр түрлі жиындардың бір шекті системасын алайық. Қарапайымдылық үшін үш жиынды – E, F, G жиындарын алсақта болады. E, F, G жиындарының системасында анықталатын қатынастарды ∆1, ∆2,..., ∆к арқылы белгілейік. Бұл қатынастарды E×F×G декарттық көбейтіндінің алдын ала берілген бөлімше жиындары ретінде қарастырмай-ақ, тек айқын тұжырымдап, берілген А1 , А2,..., Аt (1)қасиеттерді қанағаттандыруы туралы ғана талап қояйық.
Берілген қасиеттерді қанағаттандыратын 
қатынастарының системасы бір емес, бірнешеу болуы да мүмкін. мұның бір қарапайым мысалы мынадай.
∆ - нақты сандардың R жиыны үстінде анықталған алгебралық операция болсын (∆операциясын ∆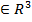 
қатынасы ретінде қарастыруға болатындығы жоғарыда айтылған), біз осы қатынастың мынадай қасиеті болуын талап етейік: 
(коммутативтік). 
жиынының үстінде болатын екі коммутативтік операция бар (басқаша айтқанда, А1 қасиеті бар ∆ қатынасының екі мәні болады), олар нақты сандардағы 
Әрқайсысының алдын ала берілген (1) қасиеттері болатын ∆1,...,∆kқатынастарының барлық 
системаларының жиынын Т арқылы белгілейік. Егер Т ≠ 
болса, онда 
элементіE, F, G жиындарының үстінде Т текті структураны (дәлірек айтқанда Т текті математикалық структураны) анықтайды дейді.
Т жиынын анықтайтын, айқын түрде тұжырымдалған қасиеттер Т текті стуктураның аксиомалары деп аталады, ал E, F, G жиындары – текті структураның базасы деп аталады. Текті бірдей бірнеше структураға бір арнайы атау беріледі. Мысалы, группалар структурасы, n өлшемді евклидтік кеңістіктің структурасы т.с.с.
Мысал: (группалар структурасы)
Базассы бір ғана Е ≠ 
жиынынан тұрады, қатынастар системасы бір ғана Δ қатынастан тұрады, ол төмендегі төрт аксиоманы қанағаттандырады:
А1:Δ қатынасы – Е жиынының үстінде анықталған алгебралық операция;
А2:Δ(Δ(a,b),c)=Δ(aΔ(b,c)), 
(ассоцитивтік);
А3: 
(бейтарап элементтердің болуы);
А4: 
(а элементіне симметриялы а/ элементінің болуы).
Белгілі текті структура анықталған жиыға арнайы атау беріледі. Сонда жоғарыда қарастырылған мысалыда біз «Е группа» дейміз, ал толық түрде айтқанда былай деу керек: «Е жиыны үстінде группа структурасының текті структурасы анықталған».
Егер база бірнеше жиыннан, мысалы үш,аиап айтқанда E, F, G жиындарынан құралса, онда әдетте олардың біреуі, мәселен Е жиыны басты роль атқарады да, қалғандары анықталатын структурада көмекші роль атқарады. Ондайда бұл структуралар Е жиынының үстінде анықталған дейді де Fпен G жиындарын көмекші жиындар ретінде қарастырады.
Мәселен берілген К үрісі үстіндегі n өлшемді векторлық кеңістіктің структурасын анықтағанда база екі жиыннан, атап айтқанда V жиыны мен К жиынынан құралады, бірақ онда К көмекші роль атқарады.
Т текті структуралар теориясы дегеніміз – әр қайсысы Т-ны анықтайтын аксиомалардың логикалық салдары болып табылатын сөйлемдердің (теоремалардың) 
жиыны. Группалар теориясы, сақиналар теориясы, аффиндік кеңістіктің теориясы, евклидтік кеңістіктің геометриясы т.с.с. осындай Т текті структуралардың теориялары болып табылады.
Математикада математикалық структуралар ғана зерттелінеді. Оның негізгі әдісі – аксиоматикалық әдіс: онда әрбір тектің структурасы өзіне сәйкес аксиомалардың тізімі бойынша анықталады, одан әрі таза жолмен логикалық сол тектің структурасының теоремасы жасалады.
Аксиомалар системасының интерпретациялары (модельдері)
Әрбір жиыны үстінде кез келген структураны анықтауға болады деп ойламау керек. Мысалы: Е={0,1,2,3,4,5}жиыны үстінде R өрісі үстіндегі n өлшемді векторлық кеңістік структурасын анықтауға болмайды,алайда ол структура 
жиыны үстінде оңай анықталады.
Сондықтан математикалық структураны анықтағанда 
жағдайы екі себептен туады, ол себептер мынандай:
а) берілген база қажетті текті структураны құруға мүмкіндік бермейді, бірақ базаны басқа бір жолмен таңдап алғанда структура құрылады;
б) қажетті структураны құруға мүмкіндік беретін база болмайды (базақалай алынса да, бола береді).
Соңғы жағдайда Т жиынын анықтайтын А1 , А2,..., Аt аксиомалары системасының қайшылығыбар дейді. Ал егер қарастырылған структураны анықтайтын база болса (демек, 
болса), онда ол аксиомалар системасын қайшылықсыз дейді.
∆1, ∆2,..., ∆к қатынастарына нақты мағына берерліктей және А1 , А2,..., Аt аксиомалары оындалатын бір нақты М жиыны табылады делік. Ондайда А1 , А2,..., Аt аксиомалар системасының интерпретациясы құрылды дейді де, М жиынының өзән Т текті структураның моделі дейді.
Мысалы. М жиыны элементтері нақты сндар болатын екінші ретті квадрат матрицалар жиыны болсын. Әдеттегі әдіспен матрицаларды қосу және оларды R өрісіндегі нақты сандарға көбейту операциларын қолданып, М жиыны нақты сандардың R өрісі үстіндегі 4 өлшемді векторлық кеңістіктің моделі болатындығын көреміз.
Сонымен, А1 , А2,..., Аt аксиомалар системасының қайшылықсыздығын дәлелдеу үшін оның әйтеуір бір интерпретациясын құру жеткілікті болады.
Ескертпе. Егер Т текті структураларды анықтайтын база болса, онда ол текті структуралардың А1 , А2,..., Аt аксиомалар системасы қайшылықсыз система деп аталады дедік. Кейде аксиомалардың мұндай системасын мағынасы бойынша қайшылықсыз система деп атайды.
Егер системадан логикалық бірі екіншісін теріске шығарарлық екі түрлі қорытынды жасалмайтын болса, онд аксиомалардың ол системасын ішкі қайшылықсыз система деп атайды.
Сонымен, егер математикалық логика заңдары арқылы логикалық қорытынды шығару техникасын зерттеп қарастырмай, тек геометрия мәселелерімен шектелсек, біз аксиомалардың берілген системасының мағынасы бойынша қайшылықсыздығы жөніндегі мәселені ғана шеше аламыз.
