2.1. Локальный экстремум функции
Пусть функция f определена в некоторой окрестности точки х0, х0  .
.
 Определение. Точку х0 назовем точкой локального максимума (локального минимума) функции f, если существует δ > 0 такое, что для всякого х, принадлежащего интервалу (х9- δ, х0+ δ) справедливо неравенство f(х)≤ f(х0) (f(х)≥ f(х0)).
Определение. Точку х0 назовем точкой локального максимума (локального минимума) функции f, если существует δ > 0 такое, что для всякого х, принадлежащего интервалу (х9- δ, х0+ δ) справедливо неравенство f(х)≤ f(х0) (f(х)≥ f(х0)).
На рис. 4 изображен график функции, для которой х1 является точкой локального максимума, а х2 – точкой локального минимума.
Точки локального максимума и локального минимума называют точками локального экстремума функции.
Теорема 1. ( Теорема Ферма ) Если функция дифференцируема в точке её локального экстремума, то производная функции в этой точке равна нулю.
► Пусть точка х0 является точкой локального максимума функции f, и пусть f дифференцируема в этой точке. Тогда существует 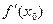 , а также односторонние производные
, а также односторонние производные  и
и  , причем
, причем 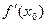
 . Найдется δ > 0 такое, что для всякого х, принадлежащего интервалу (х0 - δ, х0+ δ) справедливо неравенство f(х) ≤ f(х0). Следовательно, при х
. Найдется δ > 0 такое, что для всякого х, принадлежащего интервалу (х0 - δ, х0+ δ) справедливо неравенство f(х) ≤ f(х0). Следовательно, при х 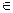 (х0 - δ, х0)
(х0 - δ, х0)  ≥ 0, а при х
≥ 0, а при х 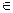 (х0 , х0+ δ)
(х0 , х0+ δ)  ≤ 0. Отсюда и из теоремы определьном переходе а неравенстве (гл.1, п. 4.5) следует:
≤ 0. Отсюда и из теоремы определьном переходе а неравенстве (гл.1, п. 4.5) следует:  =
= 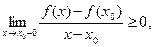
 =
=  . Но
. Но 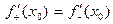 ; значит,
; значит,  , и потому
, и потому  0.
0.
В случае локального минимума доказательство аналогично. ◄
Следствие. Пусть функция f дифференцируема в точке х0 , а её производная в этой точке отлична от нуля: 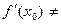 0. Тогда х0 не является точкой локального экстремума функции.
0. Тогда х0 не является точкой локального экстремума функции.
2.2. Теоремы Ролля, Коши и Лагранжа
Теорема 2 (Теорема Ролля) Пусть функция f непрерывна на сегменте [ a,b ], a<b, дифференцируема на интервале (a,b), а на его концах принимает одинаковые значения: f(a) =f(b). Тогда на интервале (a,b) существует хотя бы одна точка, производная в которой равна нулю.
► Так как f непрерывна на [ a,b ], она ограничена на нем, и на [ a,b ] существуют точки  и
и  такие,что f(
такие,что f(  ) = m, f(
) = m, f(  ) = M, где
) = M, где 
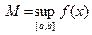 (гл. 1, п. 5.3). Очевидно, m≤ M. Если m= M, то функция тождественно на сегменте [ a,b ] равна константе, а тогда ее производная тождественно на интервале (a,b) равна нулю; следовательно, в случае m= M утверждение теоремы справедливо. Пусть теперь m < M. Так как f(a) =f(b), то хотя бы одна из точек
(гл. 1, п. 5.3). Очевидно, m≤ M. Если m= M, то функция тождественно на сегменте [ a,b ] равна константе, а тогда ее производная тождественно на интервале (a,b) равна нулю; следовательно, в случае m= M утверждение теоремы справедливо. Пусть теперь m < M. Так как f(a) =f(b), то хотя бы одна из точек  и
и  должна быть внутренней точкой сегмента, т.е. она принадлежит интервалу (a,b). Такая точка, очевидно, является точ- кой локального экстремума; по теореме Ферма производная функции в ней равна нулю.◄
должна быть внутренней точкой сегмента, т.е. она принадлежит интервалу (a,b). Такая точка, очевидно, является точ- кой локального экстремума; по теореме Ферма производная функции в ней равна нулю.◄
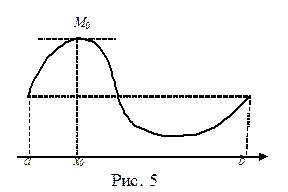 Укажем на геометрический смысл доказанной теоремы. На рис. 5 изображен график функции f, удовлетворяющей условию теоремы Ролля. В частности, значения функции в точках a и b одинаковы. Рисунок наглядно демонстрирует, что на графике имеются точки, касательная в которых параллельна оси абсцисс. Если М0 (х0,у0) - такая точка, то
Укажем на геометрический смысл доказанной теоремы. На рис. 5 изображен график функции f, удовлетворяющей условию теоремы Ролля. В частности, значения функции в точках a и b одинаковы. Рисунок наглядно демонстрирует, что на графике имеются точки, касательная в которых параллельна оси абсцисс. Если М0 (х0,у0) - такая точка, то  (см. п.1.5).
(см. п.1.5).
Теорема 3. (Теорема Коши) Пусть функции f и g непрерывны на сегменте [ a,b ], a<b, дифференцируемы на интервале (a,b), причем производная  не принимает значение нуль на этом интервале. Тогда на (a,b) существует точка ξ такая, что
не принимает значение нуль на этом интервале. Тогда на (a,b) существует точка ξ такая, что
 .
.
► Заметим: g(b) ≠ g(a). Действительно, если бы имело место равенство g(b) = g(a), то функция g удовлетворила бы условию теоремы Ролля. Значит, производная  должна была бы обратиться в нуль хотя бы одной точке интервала (a,b), что противоречит условию доказываемой теоремы.
должна была бы обратиться в нуль хотя бы одной точке интервала (a,b), что противоречит условию доказываемой теоремы.
Обозначим: 
 , F(x) = f(x) -
, F(x) = f(x) -  g(x). Нетрудно убедиться, что функция F(x) удовлетворяет на [ a,b ] всем требованиям условия теоремы Ролля. Следовательно, на интервале (a,b) найдется точка ξ, в которой производная
g(x). Нетрудно убедиться, что функция F(x) удовлетворяет на [ a,b ] всем требованиям условия теоремы Ролля. Следовательно, на интервале (a,b) найдется точка ξ, в которой производная  принимает значение нуль:
принимает значение нуль:  0. Отсюда:
0. Отсюда: 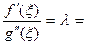
 .◄
.◄
Теорема 4. (Теорема Лагранжа) Если функция f непрерывна на сегменте [ a,b ], a<b, и дифференцируема на интервале (a,b), то на интервале (a,b) найдется точка ξтакая, что f(b) – f(a) =  (b – a).
(b – a).
► Пусть g (х) = х на сегменте [ a,b ]. Нетрудно увидеть, что функции f и g удовлетворяют всем требованиям условия теоремы Коши; значит, на интервале (a,b) най- дется точка ξ такая,что  , т.е.
, т.е.  , что и требовалось доказать. ◄
, что и требовалось доказать. ◄
 Замечание 1. Равенство
Замечание 1. Равенство
f(b) – f(a) =  (b – a)
(b – a)
называют формулой Лагранжа или формулой конечных приращений. Она имеет прозрачный геометрический смысл. В равенстве  слева стоит тангенс угла наклона к оси абсцисс хорды АВ, где А(а,f(а)), B(b,f(b)), а справа – тангенс угла наклона к оси абсцисс касательной к графику функции в точке М (ξ, f( ξ )) (рис. 6). Значит, хорда и касательная параллельны. Таким образом, утверждение теоремы Лагранжа можно сформулироватьтак: на графике функции существует точка, в которой касательная к графику параллельна хорде, стягивающей его концы.
слева стоит тангенс угла наклона к оси абсцисс хорды АВ, где А(а,f(а)), B(b,f(b)), а справа – тангенс угла наклона к оси абсцисс касательной к графику функции в точке М (ξ, f( ξ )) (рис. 6). Значит, хорда и касательная параллельны. Таким образом, утверждение теоремы Лагранжа можно сформулироватьтак: на графике функции существует точка, в которой касательная к графику параллельна хорде, стягивающей его концы.
Замечание 2. Пусть х0 – некоторая точка числовой оси, h ≠ 0, и пусть функция f непрерывна на сегменте,ограниченном точками х0 и х0 + h (здесь возможно и h> 0, и h< 0) и дифференцируема на интервале, ограниченном теми же точками. Тогда по теореме Лагранжа f(х0 + h) – f(х0) =  h, где ξ – некоторая точка, лежащая между х0 и х0 + h. Это равенство можно записать так: Δ f(h) =
h, где ξ – некоторая точка, лежащая между х0 и х0 + h. Это равенство можно записать так: Δ f(h) =  h. Так как ξ лежит между х0 и х0 + h, то можно подобрать число θ, 0 < θ < 1, так, чтобы выполнялось ξ = х0 + θ h; тогда Δ f(h) =
h. Так как ξ лежит между х0 и х0 + h, то можно подобрать число θ, 0 < θ < 1, так, чтобы выполнялось ξ = х0 + θ h; тогда Δ f(h) =  + θ h) h.
+ θ h) h.
2.3. Правило Лопиталя
Теоремы предыдущего пункта имеют многочисленные приложения в анализе. В частности, на них опирается так называемое правило Лопиталя – способ вычисления предела функции, который часто оказывается наиболее простым и эффективным.
Теорема 5. Пусть функции α и β дифференцируемы на некотором интервале (a, b), a<b, причем β′(х) ≠ 0 на (a, b), и  .
.
Если  , где А есть либо число, либо один из символов +∞, - ∞ или ∞, то и
, где А есть либо число, либо один из символов +∞, - ∞ или ∞, то и 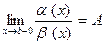 .
.
► Пусть х – точка, выбранная на (a, b). На сегменте [ х,b ] зададим две функции 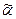 и
и  :
:
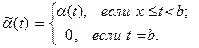 ,
, 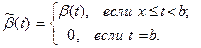 Эта пара функций удовлетворяет на сегменте [ х,b ] всем требованиям условия теоремы Коши; значит, на интервале (х,b) существует точка – обозначим её через ξ (х) - такая, что
Эта пара функций удовлетворяет на сегменте [ х,b ] всем требованиям условия теоремы Коши; значит, на интервале (х,b) существует точка – обозначим её через ξ (х) - такая, что  , т.е.
, т.е.  . Здесь х – произвольная точка интервала (х,b), и так как х < ξ (х) < b, то при
. Здесь х – произвольная точка интервала (х,b), и так как х < ξ (х) < b, то при  ξ (х) стремится к b слева. Отсюда следует:
ξ (х) стремится к b слева. Отсюда следует:
 . ◄
. ◄
Теорема 6. Пусть функции α и β дифференцируемы на некотором интервале (a, b), a<b, причем β′(х) ≠ 0 на (a, b), и  . Если
. Если  , где А есть либо число, либо один из символов +∞, - ∞ или ∞, то и
, где А есть либо число, либо один из символов +∞, - ∞ или ∞, то и  .
.
Доказатедьство этой теоремы вполне аналогично доказательству теоремы 5.
Теорема 7. Пусть функции α и β дифференцируемы в некоторой проколотой окрестности  точки х0
точки х0  , причем β′(х) ≠ 0 в
, причем β′(х) ≠ 0 в  ,и
,и 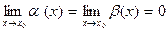 . Если
. Если  , где А есть либо число, либо один из символов +∞, - ∞ или ∞, то и
, где А есть либо число, либо один из символов +∞, - ∞ или ∞, то и  .
.
► Множество 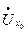 представляет собой обьединение двух интервалов (a, х0) и (х0 , b), где a и b - некоторыечисла такие, что a < х0 < b. Так как
представляет собой обьединение двух интервалов (a, х0) и (х0 , b), где a и b - некоторыечисла такие, что a < х0 < b. Так как  , то
, то 
 . Применив к (a, х0) теорему 5, а к (х0 , b) теорему 6, получим:
. Применив к (a, х0) теорему 5, а к (х0 , b) теорему 6, получим:  и
и  ; значит,
; значит,  . ◄
. ◄
Пример 1. Вычислить  .
.
► В проколотой окрестности нуля  = (-1,0)
= (-1,0)  (0,1) числитель α(х) = tgx – x и знаменатель β(x) = arcsinx – ln(1+x) дифференцируемы, а производная β′(x) не принимает значение 0: при х
(0,1) числитель α(х) = tgx – x и знаменатель β(x) = arcsinx – ln(1+x) дифференцируемы, а производная β′(x) не принимает значение 0: при х  (-1,0)
(-1,0)  (0,1)
(0,1)
 Кроме того,
Кроме того,  , и
, и  По теореме 7 искомый предел
По теореме 7 искомый предел 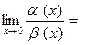
 . ◄
. ◄
Если в тексте теоремы 5 заменить интервал (a, b) на интервал (a,+∞), а символ  на символ
на символ 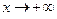 , то получится формулировка теоремы, справедливость которой можно доказать ([3], § 12, п.1). Приведем пример её применения.
, то получится формулировка теоремы, справедливость которой можно доказать ([3], § 12, п.1). Приведем пример её применения.
Пример 2. Вычислить  .
.
► Числитель α(х) = π – arctgx и знаменатель β(x) = ln 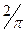 arctgx дифференцируемы на (0,+∞), а производная β′(x) =
arctgx дифференцируемы на (0,+∞), а производная β′(x) = 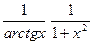 не прини- мает значение 0 на этом интервале. Кроме того,
не прини- мает значение 0 на этом интервале. Кроме того,  , а
, а

 .
.
Значит, искомый предел также равен –π. ◄
Справедливы теоремы, аналогичные теоремам 6 и 7. Формулировку одной из них можно получить, заменив в формулировке теоремы 6 интервал (a, b) на (- ∞, b ), а символ  на
на 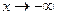 . Другая теорема получается при замене в тексте теоремы 7 проколотой окрестности
. Другая теорема получается при замене в тексте теоремы 7 проколотой окрестности 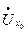 окрестностью бесконечности и
окрестностью бесконечности и  символом
символом  .
.
Выше правило Лопиталя (предел отношения функций равен пределу отношения их производных) применялось для вычисления предела отношения двух бесконечно малых. Это правило применяется и при вычислении предела отношения двух бесконечно больших. Чтобы получить формулировки теорем, на которых оно основывается в случае бесконечно больших функций, нужно в формулировках приведенных выше теорем полагать функции α и β бесконечно большими. Для примера приведем формулировку теоремы, аналогичной теореме 5: пусть функции α и β дифференцируемы на интервале (a, b), a<b, причем β′(х) ≠ 0 на (a, b), и 
 . Если
. Если  , где А есть либо число, либо один из символов +∞, - ∞ или ∞, то и
, где А есть либо число, либо один из символов +∞, - ∞ или ∞, то и 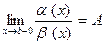 .
.
Пример 3. Вычислить  и
и 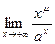 , где a > 1, μ > 0.
, где a > 1, μ > 0.
► Здесь числители и знаменатели являются бесконечно большими при х→ +∞. Они дифференцируемы на (0, +∞), причем производные знаменателей не принимают на этом интервале значение 0. Имеем:  .
.  . Если 0 < μ ≤ 1, то последний предел равен, очевидно, нулю; значит, при 0 < μ ≤ 1
. Если 0 < μ ≤ 1, то последний предел равен, очевидно, нулю; значит, при 0 < μ ≤ 1 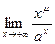 = 0. Если же μ > 1, то
= 0. Если же μ > 1, то  есть предел отношения двух бесконечно больших, и можно снова приме- нить правило Лопиталя:
есть предел отношения двух бесконечно больших, и можно снова приме- нить правило Лопиталя:  =
=  . Если 1 < μ ≤ 2, то последний предел равен нулю; значит(с учетом предыдущего результата), при 0 < μ≤ ≤ 2
. Если 1 < μ ≤ 2, то последний предел равен нулю; значит(с учетом предыдущего результата), при 0 < μ≤ ≤ 2 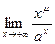 = 0. Если же μ > 2, то
= 0. Если же μ > 2, то  есть предел отношения двух бесконечно больших, и мы вновь обращаемся к правилу Лопиталя.
есть предел отношения двух бесконечно больших, и мы вновь обращаемся к правилу Лопиталя.
Таким образом, для любого μ > 0, применив правило Лопиталя n+1 раз, где n есть целая часть μ, получим: 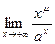 = 0. ◄
= 0. ◄
В теоремах и рассмотренных выше примерах правило Лопиталя применялось для вычисления предела отношения двух бесконечно малых или или двух бесконечно больших функций. В других ситуациях, чтобы можно было воспользоваться этим правилом, следует предварительно преобразовать выражение под знаком предела так, чтобы свести задачу к отысканию предела отношения двух бесконечно малых или или двух бесконечно больших функций.
Пример 4. Вычислить  .
.
► Имеем:  =
=  . Вычислим
. Вычислим  . Чтобы можно было воспользоваться правилом Лопиталя, преобразуем выражение под знаком предела:
. Чтобы можно было воспользоваться правилом Лопиталя, преобразуем выражение под знаком предела:  . Предел отношения двух бесконечно больших находим по правилу Лопиталя:
. Предел отношения двух бесконечно больших находим по правилу Лопиталя: 
 . Итак,
. Итак,  =
=  =
=  = 1. ◄
= 1. ◄
2.4. Формула Тейлора
Пусть n – натуральное число, большее единицы, а х0 – вещественное число.
Определение. Будем говорить, что функция f n раз дифференцируема в точке х0, если эта функция, а также её производные до порядка n- 1 включительно дифференцируемы в точке х0 .
Функция, дифференцируемая в точке, определена в некоторой её окрестности,, причем в этой точке существует производная функции (см. п.1.2). Следовательно, если функция f n раз дифференцируема в точке х0, то она и ее производные до порядка n- 2 включительно дифференцируемы в некоторой окрестности этой точки, а производная порядка n- 1 дифференцируема по крайней мере в точке х0.. Заметим еще, что n – крат- ная дифференцируемость f в точке х0 эквивалентна существованию в этой точке производных функции до порядка n включительно.
Ради единообразия будем говорить, что функция, дифференцируемая в точке х0 (см. определение в п.1.2), дифференцируема в этой точке один раз.
Пусть функция f n раз, где n – любое натуральное число, дифференцируема в точке х0, Обозначим: t0 = f(x0); tk = 
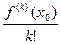 , где k = 1, …, n;
, где k = 1, …, n;
Tn(x) = t0 + t1(x-x0) +…+ tn(x-x0) 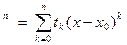 .
.
Числа tk, k = 0, 1, …, n, называют коэффициентами Тейлора функции f. Очевидно, Tn(x) представляет собой алгебраический многочлен степени не выше n; его называют многочленом Тейлора функции f. Нетрудно убедиться, что в точке х0 значения многочлена Tn(x) и его производных до порядка n включительно совпадают со значениями в этой точке функции f и её соответствующих производных:
Tn(x0) = f(х0); T 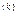 n(x0) =
n(x0) = 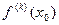 при k = 1, …, n. (8) Еще одно свойство многочлена Тейлора описано в следующей теореме.
при k = 1, …, n. (8) Еще одно свойство многочлена Тейлора описано в следующей теореме.
Теорема 8. (Теорема Тейлора-Пеано) Пусть функция f n раз, где n – любое натуральное число, дифференцируема в точке х0 , Тогда справедлива асимптотическая формула:
f (х) = Tn(x) + о((х-х0)  ), х→х0. (9)
), х→х0. (9)
► Пусть сначала n= 1, т.е. f дифференцируема в точке х0 (п.1.2):
Δ f(h) = f(x0+h) – f(x0) =  + o(h). Положив здесь h = x –x0, получим: f(x) – f(x0) =
+ o(h). Положив здесь h = x –x0, получим: f(x) – f(x0) = 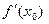 (х-х0)+ o(х-х0). Отсюда, так как T1(x) = f(x0) +
(х-х0)+ o(х-х0). Отсюда, так как T1(x) = f(x0) + 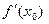 (х-х0), следует: f (х)=T1(x) + о((х-х0)), х→х0 . и теорема доказана для случая n= 1.
(х-х0), следует: f (х)=T1(x) + о((х-х0)), х→х0 . и теорема доказана для случая n= 1.
Пусть теперь n> 1. Обозначим: rn (x) = f (х) - Tn(x). Требуется доказать, что rn (x) = о((х-х0)  ), х→х0, т.е. что
), х→х0, т.е. что 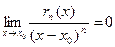 .Заметим: так как f (х) n раз дифференцируема,то и rn (x) обладает тем же свойством, причем из (8) следуют равенства
.Заметим: так как f (х) n раз дифференцируема,то и rn (x) обладает тем же свойством, причем из (8) следуют равенства
rn (x0) = 0; rn 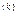 (x0) = 0 при k = 1, …, n. (10)
(x0) = 0 при k = 1, …, n. (10)
Обозначим: α(х) = rn (x), β(х) = (х-х0)  . Нетрудно убедиться, что эта пара функций удовлетворяет в окрестности x0 всем требованиям условия теоремы 7; значит, если
. Нетрудно убедиться, что эта пара функций удовлетворяет в окрестности x0 всем требованиям условия теоремы 7; значит, если  есть либо число, либо один из символов +∞, - ∞ или ∞, то
есть либо число, либо один из символов +∞, - ∞ или ∞, то  =
=  , т.е., если существует конечный или бесконечный предел
, т.е., если существует конечный или бесконечный предел  , то
, то  =
=  . Снова введем две функции α(х) = r′n (x) и β(х) = n (х-х0)
. Снова введем две функции α(х) = r′n (x) и β(х) = n (х-х0) 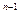 и применим к ним теорему 7: если существует конечный или бесконечный предел
и применим к ним теорему 7: если существует конечный или бесконечный предел  =
=  ,то
,то  =
=  и, значит,
и, значит,  =
=  .
.
Повторив это рассуждение n- 1 раз, придем к выводу: если существует конечный или бесконечный предел 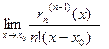 , то
, то
 =
= 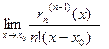 . (11)
. (11)
Функция α(х) = 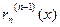 дифференцируема в точке х0, поэтому α(х)- α(х0) = = α′(х0) (х-х0) +о(х-х0), т.е.
дифференцируема в точке х0, поэтому α(х)- α(х0) = = α′(х0) (х-х0) +о(х-х0), т.е. 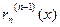 -
-  =
= 
 . Но
. Но  =
= 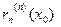 = 0 (см. (10)); значит,
= 0 (см. (10)); значит, 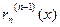 =
=  . После подстановки в (11), получим:
. После подстановки в (11), получим:
 =
= 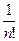
 = 0, что и требовалось доказать. ◄
= 0, что и требовалось доказать. ◄
Равенство (9) называют разложением функции f по формуле Тейлора в окрестности точки х0; слагаемое о((х-х0)  ) называют остаточным членом этой формулы. Ее называют также формулой Тейлора порядка n c остаточным членом в форме Пеано.
) называют остаточным членом этой формулы. Ее называют также формулой Тейлора порядка n c остаточным членом в форме Пеано.
Таким образом, разность между функцией f (х) и ее многочленом Тейлора Tn(x) яаляется при х →х0 бесконечно малой, порядок которой выше n. Заметим,что среди всевозможных алгебраических многочленов степени не выше n таким свойством обладает только многочлен Tn(x). Точнее, справедлива следующая теорема.
Теорема 9. (О единственности многочлена наилучшего приближения). Пусть f - -функция, n раз дифференцируемая в точке х0, а Рn (x) – некоторый алгебраический многочлен степени не выше n. Если справедливо асимптотическое представление
f(х) = Рn (x) + о((х-х0)  ). то Рn (x) есть многочлен Тейлора Tn(x) функции f(х).
). то Рn (x) есть многочлен Тейлора Tn(x) функции f(х).
► По условию теоремы f(х) = Рn (x) + о((х-х0)  ). Кроме того, в силу теоремы Тейлора - Пеано f (х) = Tn(x) + о((х-х0)
). Кроме того, в силу теоремы Тейлора - Пеано f (х) = Tn(x) + о((х-х0)  ). Вычитая одну формулу из другой, получим: Tn(x) - Рn (x) = о((х-х0)
). Вычитая одну формулу из другой, получим: Tn(x) - Рn (x) = о((х-х0)  ). Отсюда следует: при х →х0
). Отсюда следует: при х →х0
Tn(x) - Рn (x) → 0 и 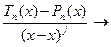 0, j = 1,2, …, n. (12) Имеем: Tn(x) =
0, j = 1,2, …, n. (12) Имеем: Tn(x) =  , Рn (x)=
, Рn (x)= 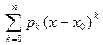 ;
;
Tn(x) - Рn (x) = (t0 –p0) +(t1 –p1) (x-x0) + (t2 –p2) (x-x0)  + …+ (tn -pn) (x-x0)
+ …+ (tn -pn) (x-x0)  .
.
Отсюда и из Tn(x) - Рn (x) → 0 следует: t0 –p0 = 0, т.е. t0 = p0 . Значит,
Tn(x) -Рn (x)= (t1 –p1) (x-x0) + (t2 –p2) (x-x0)  +(t3 –p3)(x-x0)
+(t3 –p3)(x-x0)  +…+ (tn -pn) (x-x0)
+…+ (tn -pn) (x-x0)  ;
;
 (t1 –p1) + (t2 –p2) (x-x0) +(t3 –p3)(x-x0)
(t1 –p1) + (t2 –p2) (x-x0) +(t3 –p3)(x-x0)  …+ (tn -pn) (x-x0)
…+ (tn -pn) (x-x0) 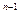 . Так как
. Так как  0, то t1 –p1 = 0, т.е. t1 = p1. Следовательно,
0, то t1 –p1 = 0, т.е. t1 = p1. Следовательно,
 (t2 –p2) (x-x0) +(t3 –p3)(x-x0)
(t2 –p2) (x-x0) +(t3 –p3)(x-x0)  + …+ (tn -pn) (x-x0)
+ …+ (tn -pn) (x-x0) 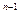 ;
;
 (t2 –p2) +(t3 –p3)(x-x0) +…+ (tn -pn) (x-x0)
(t2 –p2) +(t3 –p3)(x-x0) +…+ (tn -pn) (x-x0)  . Отсюда, так как
. Отсюда, так как 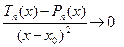 , следует t2 =p2..
, следует t2 =p2..
Продолжая описанный процесс и используя равенства (12), в итоге докажем равенства tk = pk, k = 1,2, …, n. Значит, Tn(x)≡ Рn (x). ◄
Приведем несколько примеров разложений функций по формуле Тейлора в окрестности х0 = 0. Такие разложения называют также разложениями (формулами) Маклорена.
Пример 5, Пусть f(х)=  , х0 = 0.
, х0 = 0.
Эта функция имеет производные любого порядка; поэтому для нее формулу (9) можно записать при любом натуральном n. Пусть k – неко- торое натуральное число; имеем: f 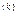 (х)=
(х)=  . Найдем коэффициенты Тейлора: t0 = f( 0 )=
. Найдем коэффициенты Тейлора: t0 = f( 0 )=  =1; при всяком натуральном k tk =
=1; при всяком натуральном k tk =  .
.
Пусть n – любое натуральное число Запишем многочлен Тейлора степени n: Tn(x) = 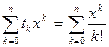 =
=  . Таким образом, разложение порядка n функции f(х)=
. Таким образом, разложение порядка n функции f(х)=  в окрестности х0 = 0 выглядит так:
в окрестности х0 = 0 выглядит так:
 =
= 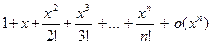 .
.
Пример 6. Пусть f(х)= sinx, х0 = 0.
При любом натуральном k  (см., нпример, [3], п. 11.1). Найдем коэффициенты Тейлора: t0 = f( 0 )= sin 0 = 0; при k ≥ 1
(см., нпример, [3], п. 11.1). Найдем коэффициенты Тейлора: t0 = f( 0 )= sin 0 = 0; при k ≥ 1
tk = 
Пусть n – любое натуральное число. Запишем формулу Маклорена порядка 2 n для функции sinx: sinx = 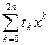 + o(
+ o( ), т.е.
), т.е.
sinx =  .
.
Пример 7. Пусть f(х)=cos x, х0 = 0.
При любом натуральном k 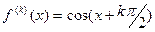 . Найдем коэффециенты Тейлора: t0 = f( 0 )= cos 0 = 1; при k ≥ 1
. Найдем коэффециенты Тейлора: t0 = f( 0 )= cos 0 = 1; при k ≥ 1
tk = 
Пусть n – любое натуральное число. Запишем формулу Маклорена порядка 2 n+ 1для функции cosx: cosx = 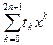 + o(
+ o( ), т.е.
), т.е.
cosx =  .
.
Пример 8. Пусть f(х)=ln(1+x), х0 = 0.
Методом математической индукции нетрудно проверить: при всяком натуральном k 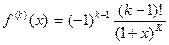 . Значит, t0 = f( 0 ) = 0, при всяком натуральном k tk =
. Значит, t0 = f( 0 ) = 0, при всяком натуральном k tk =  . Пусть n – любое натуральное число. Запишем формулу Маклорена порядка n: ln(1+x) =
. Пусть n – любое натуральное число. Запишем формулу Маклорена порядка n: ln(1+x) = 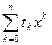 + o(
+ o(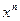 ), т.е.
), т.е.
ln(1+x) =  .
.
Пример 9. Пусть f(х)=(1+x) 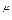 , где μ – любое вещественное число, х0 = 0.
, где μ – любое вещественное число, х0 = 0.
Методом математической индукции нетрудно проверить: при всяком натуральном k  . Найдем коэффециенты Тейлора: t0 = f( 0 )= 1; при k ≥ 1 tk =
. Найдем коэффециенты Тейлора: t0 = f( 0 )= 1; при k ≥ 1 tk =  . Пусть n – любое натуральное число. Запишем формулу Маклорена порядка n: (1+x)
. Пусть n – любое натуральное число. Запишем формулу Маклорена порядка n: (1+x) 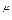 =
= 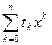 + o(
+ o(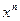 ), т.е.
), т.е.
(1+x) 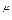 =
=  .
.
Пусть функция f дифференцируема n раз в точке х0 , причем f(х0) = 0. Тогда функция f является бесконечно малой при х → х0 , t0 = f( 0 )= 0, и формула (8) принимает вид:
f (x) = t1(х-х0) + t2(x-x0)  +…+ tn(x-x0)
+…+ tn(x-x0)  + о((х-х0)
+ о((х-х0)  ). Среди коэффициентов t1, t2, …, tn также могут оказаться равные нулю; не исключен и такой случай, когда все они равны нулю. Таким образом, если функция f является бесконечно малой при х → х0 , возможны два случая: либо найдется натуральное р, 1≤ р ≤ n, такое,что tk = 0, k = 0,1, …, p- 1, a t р≠ 0, либо все коэффициенты t1, t2, …, tn равны нулю.В первом случае
). Среди коэффициентов t1, t2, …, tn также могут оказаться равные нулю; не исключен и такой случай, когда все они равны нулю. Таким образом, если функция f является бесконечно малой при х → х0 , возможны два случая: либо найдется натуральное р, 1≤ р ≤ n, такое,что tk = 0, k = 0,1, …, p- 1, a t р≠ 0, либо все коэффициенты t1, t2, …, tn равны нулю.В первом случае
f (x) = tр(х-х0)  + tр+1(x-x0)
+ tр+1(x-x0)  +…+ tn(x-x0)
+…+ tn(x-x0)  + о((х-х0)
+ о((х-х0)  )=
)=
= tр(х-х0)  + о((х-х0)
+ о((х-х0)  ); значит, при х → х0 f (x) является бесконечно малой порядка р, а tр(х-х0)
); значит, при х → х0 f (x) является бесконечно малой порядка р, а tр(х-х0)  есть её главная часть. Во втором случае, очевидно, порядок бесконечно малой f (x) выше n. Из сказанного видно, что разложения по формуле Тейлора могут быть использованы для определения порядка бесконечно малых и выделения их главных частей.
есть её главная часть. Во втором случае, очевидно, порядок бесконечно малой f (x) выше n. Из сказанного видно, что разложения по формуле Тейлора могут быть использованы для определения порядка бесконечно малых и выделения их главных частей.
Пример 10. Вычислить 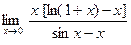 .
.
► Воспользуемся разложением примера 6:  . Отсюда:
. Отсюда:  ; значит, главная часть знаменателя есть -
; значит, главная часть знаменателя есть -  . Воспользуемся разложением примера 8:
. Воспользуемся разложением примера 8:  ; отсюда:
; отсюда:  . Значит, главная часть числителя есть
. Значит, главная часть числителя есть  . Заменив числитель и знаменатель их главными частями, получим:
. Заменив числитель и знаменатель их главными частями, получим:
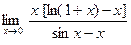 =
=  . ◄
. ◄
Разложения по формуле Тейлора широко используются в приближенных вычислениях. Из представления (9) следует, что при х, близких к х0, f(x) “почти не отличается” от Tn(x); значит, Tn(x) может быть принято в качестве приближенного значения f(x). Однако, формула (9) не дает возможности оценить погрешность приближенного равенства f(x) ≈ Tn(x). В приведенной ниже теореме к функции f предьявляются более жесткие сравнительно с теоремой 8 требования, зато остаточный член формулы Тейлора записан в виде, удобном для получения оценки погрешности.
Теорема 10. (Теорема Тейлора - Лагранжа) Пусть функция f n + 1раз дифференгцируема в некоторой окрестности  точки х0, х0
точки х0, х0  . Тогда для всякого х, х
. Тогда для всякого х, х 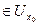 , х ≠ х0, найдется ξ, лежащее между х и х0, такое что справедливо равенство: f (х) - Tn(x) =
, х ≠ х0, найдется ξ, лежащее между х и х0, такое что справедливо равенство: f (х) - Tn(x) =  .
.
► Пусть х 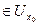 , и пусть для определенности х > х0 . На сегменте [ х0, х ] определим две функции φ и ψ: при z
, и пусть для определенности х > х0 . На сегменте [ х0, х ] определим две функции φ и ψ: при z 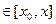
 .
.
Эти функции удовлетворяют на сегменте [ х0, х ] всем требованиям условия теоремы Коши (теоремы 3). Следовательно, существует ξ 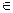 [ х0, х ] такое, что
[ х0, х ] такое, что 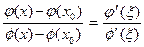 . т.е.
. т.е.  .
.
При z 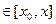 имеем:
имеем:
φ′ (z) = -  = -
= - 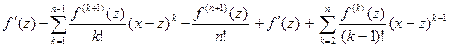 Суммы
Суммы  и
и  состоят из одних и тех же слагаемых, эти суммы одинаковы; поэтому после сокращений получим: φ′ (z) = -
состоят из одних и тех же слагаемых, эти суммы одинаковы; поэтому после сокращений получим: φ′ (z) = - 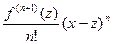 . Следовательно, φ′ (ξ) = -
. Следовательно, φ′ (ξ) = -  . Заметим еще:
. Заметим еще:  . Подставив φ′ (ξ) и ψ′ (ξ) в равенство
. Подставив φ′ (ξ) и ψ′ (ξ) в равенство  (см. выше), окончательно получим: f (х) - Tn(x) =
(см. выше), окончательно получим: f (х) - Tn(x) =  .
.
В случае х < х0 доказательство аналогично. ◄
Приведем пример применения этой теоремы.
Пример 11. Найдем приближенное значеиие 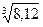 . Положим f(x)= =
. Положим f(x)= = 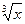 , х = = 8,12, х0 = 8, и запишем формулу Тейлора-Лагранжа при n= 1:
, х = = 8,12, х0 = 8, и запишем формулу Тейлора-Лагранжа при n= 1: 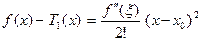 , т.е.
, т.е. 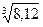
 , где ξ – некоторое число, 8 < ξ < 8,12. Подсчитаем
, где ξ – некоторое число, 8 < ξ < 8,12. Подсчитаем  . Имеем:
. Имеем: 
 , т.е.
, т.е.  = 2 +
= 2 +  . Таким образом,
. Таким образом, 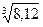 ≈ ≈
≈ ≈  (см. также пример 12, § 1). Оценим погрешность этого равенства. Имеем:
(см. также пример 12, § 1). Оценим погрешность этого равенства. Имеем:  , т.е. |
, т.е. | 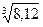 -
-  | =
| =  . Отсюда, так как 8 < ξ < 8,12: |
. Отсюда, так как 8 < ξ < 8,12: | 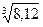 -
-  |
|  = 0,00005. Итак, абсолютная погрешность приближенного равенства
= 0,00005. Итак, абсолютная погрешность приближенного равенства 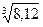 ≈
≈  не превышает 0,00005.
не превышает 0,00005.
2.5. Дифференциалы высших порядков
Если функция f дифференцируема в точке х0, то для её приращения  справедливо асимптотическое представление
справедливо асимптотическое представление  (h) = Аh + o(h), где A = f′(x0) (см. п.1.4). Покажем, что если функция f n, n> 1, раз дифференцируема в точке х0 , то существует единственный набор чисел A1, A2, …, An такой, что для её приращения
(h) = Аh + o(h), где A = f′(x0) (см. п.1.4). Покажем, что если функция f n, n> 1, раз дифференцируема в точке х0 , то существует единственный набор чисел A1, A2, …, An такой, что для её приращения  справедливо асимптотическое представление
справедливо асимптотическое представление  (h) =
(h) =  .
.
Действительно, пусть функция f определена в окрестности  = (α, β), α <
= (α, β), α < 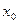 < <β, и n, n> 1, раз дифференцируема в точке х0. Запишем для неё формулу Тейлора – Пеано порядка n:
< <β, и n, n> 1, раз дифференцируема в точке х0. Запишем для неё формулу Тейлора – Пеано порядка n:
 . Положим h =
. Положим h = 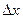 = x - x0, x = x0 + h; так как
= x - x0, x = x0 + h; так как 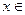 (α, β), то
(α, β), то 
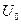 = (α -
= (α - 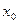 , β -
, β - 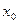 ). Перенеся f(x0) налево, получим:
). Перенеся f(x0) налево, получим:
 Мы получили представление
Мы получили представление  (h) =
(h) =  , в котором
, в котором 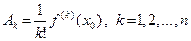 . Его единственность вытекает из теоремы 9 предыдущего пункта. Заметим, что первое слагаемое в правой части этого представления есть дифференциал df(h).
. Его единственность вытекает из теоремы 9 предыдущего пункта. Заметим, что первое слагаемое в правой части этого представления есть дифференциал df(h).
Определение. Дифференциалом порядка k, k = 2,3, …, n, функции f в точке х0 назовем выражение 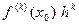 , где h принимает значения в окрестности точки 0:
, где h принимает значения в окрестности точки 0: 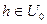
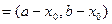 .
.
.
Обозначать дифференциал порядка k функции f в точке х0 будем символом  , а также символом
, а также символом  (h). Таким образом,
(h). Таким образом,
 (h)
(h) 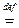
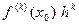 . k = 2,3, …n. Ради единообразия и удобств при записи формул дифференциал df(h) =
. k = 2,3, …n. Ради единообразия и удобств при записи формул дифференциал df(h) = 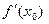 h часто называют дифференциалом первого порядка, обозначая его через
h часто называют дифференциалом первого порядка, обозначая его через  или
или  (h). Тогда для приращения n раз дифференцируемой функции можно записать представление через дифференциалы:
(h). Тогда для приращения n раз дифференцируемой функции можно записать представление через дифференциалы:  .
.
Основные свойства дифференциалов высших порядков вытекают непосредственно из свойств производных высших порядков: пустьфункции f и g n, n> 1, раз дифференцируемы в точке х0 ; тогда
1. 
2.  3.
3.  (здесь сомволы
(здесь сомволы  и
и  означают f(x0) и g(x0) соответственно),
означают f(x0) и g(x0) соответственно),
Свойством инвариантности формы дифференциалы высших порядков не обладают.






