Пусть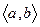 
, a < b, – произвольный промежуток, ограниченный или неограниченный, а функция f дифференцируема на нем. Определим на этом промежутке новую функцию g: для всякой внутренней точки х положим g(х) = 
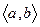(х); если точки a принадлежит , то g(а)= 
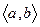; если b принадлежит , то g(b)= 
. Функцию g, определенную на 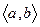описанным способом называют производной функцией от функции f или, проще, - производной функции f и обозначают символами , 
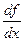
(х), 
.
Опираясь на примеры, рассмотренные в п.п.1 и 3, можно сделать следующие выводы.
Если функция тождественно на промежутке 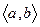равна константе, то ее производная равна нулю тождественно на этом промежутке (это часто выражают записью 
). Для показательной функции 
имеем: 
на (- ∞, + ∞); в частности, при а = е отсюда следует 
. Для степенной функции 
, где μ –любое вещественное число, на интервале (0,+ ∞) 
; при некоторых μ, например, при μ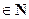 
, это равенство справедливо на всей числовой оси. Для логарифмической функции 
на (0,+ ∞) 
; При а = е отсюда следует: 
на (0,+ ∞). На всей числовой оси 
. На каждом из интервалов 
, имеем: 
, а на каждом из интервалов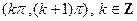 
. На интервале (-1,1) 
(пример 10). Так как при всяком х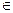 
(-1,1) arcsinx + arccosx = 
(гл. 1, п. 5.6), то arccosx = - arcsinx, и по теореме 3 
. Отсюда: на (-1,1) 
. На всей числовой оси 
(пример 11). При любых х arctgx + arcctgx = (гл. 1, п. 5.6). Отсюда
: 
.
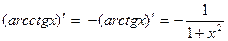1.8. Производные высших порядков
Пусть 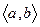, a < b, – произвольный промежуток, ограниченный или неограниченный, а функция f дифференцируема на нем. Тогда на 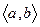, определена производная . Функция может оказаться дифференцируемой на 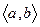. В таком случае на 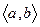определена производная функции . Эту производную называют производной второго порядка функции f и обозначают символами 
.
Пример 13. На (- ∞, + ∞) имеем: 
Функция cosx, в свою очередь, дифференцируема на (- ∞, + ∞), и 
. Значит, функция – sinx является производной второго порядка функции sinx:
.
Производную функции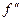 
называют производной третьего порядка функции f. Вообще, при всяком натуральном n > 1 производной порядка n функции f называют производную производной порядка n – 1 этой функции.Производную порядка n функции f обозначают символами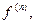 
, 
. Ради единообразия производную функции f часто называют производной первого порядка функции f.
С помощью метода математической индукции можно доказать справедливость следующих утверждений: пусть функции f и g имеют на промежутке 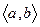производные до порядка n, n > 1, включительно; тогда сумма и произведение этих функций также имеют на 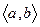производные до порядка n включительно, причем 
, где С 
; 
, где 
.
Приведем доказательство последнего утверждения по методу математической индукции (см.гл. 1, п.2.5). Равенство есть утверждение А(n); нужно доказать его справеждливость при всех натуральных n. При n= 1 имеем: А (1) есть равенство: 
; в силу теоремы 3 оно справедливо. Пусть теперь n – некоторое натуральное число; допустим, что А(n) справедливо, т.е. 
. Взяв производную от обеих его частей, получим: 
Заметим: 
; следовательно,
Но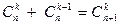 
(см. [1], стр. 12). Значит,
.
Таким образом, из допущения “ A(n) справедливо” вытекает справедливость A(n +1 ). Следовательно, установлена справедливость A(n) при всех натуральных n.
