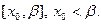1. d(f+g) = df + dg;
2. d(f g) = f(x0) dg + g(x0) df;
3. если g(x0)  0, то
0, то  .
.
Если функции f и g удовлетворяют требованиям, указанным в условии теоремы 4 о производной сложной функции, то для суперпозиции  имеем в точке х0 : dF =
имеем в точке х0 : dF = 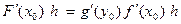 , где у0 = f(x0).
, где у0 = f(x0).
Опишем свойство дифференциала, которое называют инвариантностью (неизменностью) его формы..
Пусть х0 – некоторое число, а функция φ определена в окрестности  равенством φ(х) = х. Приращение и дифференциал этой функции назовем приращением и дифференциалом независимой переменной х и обозначим через Δ х и dx соответственно. Заметим:
равенством φ(х) = х. Приращение и дифференциал этой функции назовем приращением и дифференциалом независимой переменной х и обозначим через Δ х и dx соответственно. Заметим:  φ(х0+h) – φ(x0) =(х0+h) – x0 = h; а так как φ′(x) = 1, то dx = φ′(x0) h = h;значит, приращение независимой переменной х равно её дифференциалу:
φ(х0+h) – φ(x0) =(х0+h) – x0 = h; а так как φ′(x) = 1, то dx = φ′(x0) h = h;значит, приращение независимой переменной х равно её дифференциалу:  dx.
dx.
Пусть переменная у является функцией переменной х, дифференцируемой в точке х0: y =у(x), где у(х) - функция, дифференцируемая в точке х0 . Дифференциал функции у(х) назовем дифференциалом зависимой переменной у и обозначим через dy: dy = y′(x0) h. Здесь h – приращение аргумента (независимой переменной) х, значит (см. выше), можно записать и dy = y′(x0) Δ х, и dy = y′(x0) dx. Последнее равенство позволяет сформулировать следующее правило написания дифференциала: дифференциал зависимой переменной равен произведению её производной на дифференциалеё аргумента.
Пусть переменная z является функцией переменной у: z = z(у), и пусть эта функция дифференцируема в точке у0 = y(x0). Тогда z представляет собой сложную функцию независимой переменной х: z = z(у(х)) = F(x), В силу теоремы о производной сложной функции, F дифференцируема в точке x0, причем F′(x0) = z′(y0) y′(x0). Запишем дифференциал переменной z: dz = F′(x0) dx = z′(y0) y′(x0) dx. Но y′(x0) dx = dy, значит, dz = z′(x0) dу, т.е. дифференциал dz зависимой переменной z = z(у) равен произведению её производной z′(у0) на дифференциал dу её аргумента у. Таким образом, правило написания дифференциала, сформулированное в предыдущем абзаце, может быть применено и здесь.
Итак, если две переменные, функция и её аргумент связаны дифференцируемой зависимостью, то дифференциал функции записывается как произведение производной функции на дифференциал её аргумента - это верно и в случае, когда аргумент является независимой переменной, и в случае, когда аргумент сам представляет собой функцию от некоторой третьей переменной. Указанное свойство и называют инвариантностью формы дифференциала.
1.5.  Геометрический смысл производной и дифференциала
Геометрический смысл производной и дифференциала
Пусть функция f определена на интервале (a,b), а γ – ее график,т.е. кривая, уравнение которой y=f(x). Пусть f(x) непрерывна в некоторой точке 
 и пусть h отлично от нуля и достаточно мало по модулю, так что
и пусть h отлично от нуля и достаточно мало по модулю, так что 
 . Точки: М0(х0 , у0), где y0=f(x0), и Мh (x0+h, f(x0+h)) лежат на графике γ (рис. 1). Прямую, проходящую через точки М0 и Мh обозначим через Δh и назовем секущей; очевидно, она не параллельна оси OУ. Углом наклона α(h) секущей Δh к оси ОХ назовем угол между этой осью и прямой Δh, заключенный в интерва- ле
. Точки: М0(х0 , у0), где y0=f(x0), и Мh (x0+h, f(x0+h)) лежат на графике γ (рис. 1). Прямую, проходящую через точки М0 и Мh обозначим через Δh и назовем секущей; очевидно, она не параллельна оси OУ. Углом наклона α(h) секущей Δh к оси ОХ назовем угол между этой осью и прямой Δh, заключенный в интерва- ле  ; он отсчитывается от оси ОХ против часовой стрелки, если α(h) > 0, и по часовой стрелке в случае. α(h) < 0. При изменении h точка Мh перемещается вдоль графика γ, что вызывает вращение Δh вокруг точки М0 и, следовательно, изменение угла α(h). Значит, α(h) можно считать функцией, определенной при h, отличных от нуля и достаточно малых по модулю, т.е. в некоторой проколотой окрестности нуля. Допустим, что существует предел этой функции при h→ 0, и обозначим его через α0: α0
; он отсчитывается от оси ОХ против часовой стрелки, если α(h) > 0, и по часовой стрелке в случае. α(h) < 0. При изменении h точка Мh перемещается вдоль графика γ, что вызывает вращение Δh вокруг точки М0 и, следовательно, изменение угла α(h). Значит, α(h) можно считать функцией, определенной при h, отличных от нуля и достаточно малых по модулю, т.е. в некоторой проколотой окрестности нуля. Допустим, что существует предел этой функции при h→ 0, и обозначим его через α0: α0  α(h). Заметим: так как α(h)
α(h). Заметим: так как α(h) 
 , то α0
, то α0 
 .
.
Определение. Прямую Δ0, которая проходит через точку М0 под углом наклона к оси ОХ, равным α0 , назовем касательной к графику γ функции f в точке М0 .
Если  α0
α0  , касательную Δ0 называют наклонной, если же α0 = =
, касательную Δ0 называют наклонной, если же α0 = =  , Δ0 называют вертикальной касательной. Вертикальную прямую, проходящую через точку М0 называют вертикальной касательной еще в двух случаях: когда
, Δ0 называют вертикальной касательной. Вертикальную прямую, проходящую через точку М0 называют вертикальной касательной еще в двух случаях: когда  α(h) =
α(h) = 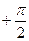 , а
, а  α(h) =
α(h) =  , и когда
, и когда  α(h) =
α(h) =  , а
, а 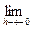 α(h) =
α(h) = 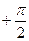 . Заметим, что в этих двух случаях
. Заметим, что в этих двух случаях 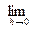 α(h) не существует.
α(h) не существует.
 Замечание 1. Касательная существует не всегда. Рассмотрим, например, функцию f(x) =|x|; её график изображен на рис.2. Пусть х0 = 0, а М0 –начало координат. При любом h > 0 точка Мh лежит на биссектрисе первого координатного угла; значит, α(h) =
Замечание 1. Касательная существует не всегда. Рассмотрим, например, функцию f(x) =|x|; её график изображен на рис.2. Пусть х0 = 0, а М0 –начало координат. При любом h > 0 точка Мh лежит на биссектрисе первого координатного угла; значит, α(h) =  при всех h > 0, а тогда
при всех h > 0, а тогда  α(h) =
α(h) =  . Аналогичные соображения приводят к равенству
. Аналогичные соображения приводят к равенству  α(h) =
α(h) = 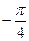 . Так как односторонние пределы различны,
. Так как односторонние пределы различны, 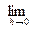 α(h) не существует; поэтому не существует и касательная в точке М0 (0,0) к изображенному на рис.2 графику...
α(h) не существует; поэтому не существует и касательная в точке М0 (0,0) к изображенному на рис.2 графику...
Замечание 2. Если касательная к графику γ функции f в точке М0 существует, то только одна - это вытекает из единственности предела α0 .
Замечание 3. Если касательная Δ0 к графику γ функции f в точке М0 существует, то при h→ 0 угол между прямыми Δ0 и Δh, т.е. разность α(h)- α0, стремится к нулю. Имея ввиду это обстоятельство, касательную называют предельным положением секущей при условии, что точка Мh стремится вдоль графика γ к точке М0 .
Пусть L – некоторая прямая, не перпендикулярная оси ОХ. Тангенс угла наклона такой прямой к оси ОХ называют угловым коэффициентом прямой L. Обозначим через k(h) угловой кoэффициент секущей Δh. Тогда (см. рис. 1)
k(h) = tg α(h) =  =
=  . (6)
. (6)
Отсюда, так как α(h) 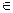
 ,
,
α(h) = arctg  . (7)
. (7)
Теорема 6. (О существовании наклонной касательной к графику) Пусть функция f определена в некоторой окрeстности точки х0, х0 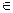 R. Для того, чтобы существовала наклонная касательная Δ0 к графику γ функции f в точке М0(х0,у0), где у0 =f(x0), необходимо и достаточно, чтобы f была дифференцируемой в точке х0.
R. Для того, чтобы существовала наклонная касательная Δ0 к графику γ функции f в точке М0(х0,у0), где у0 =f(x0), необходимо и достаточно, чтобы f была дифференцируемой в точке х0.
► Необходимость. Пусть касательная существует, т.е. 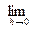 α(h)= α0 . Так как тангенс – непрерывная функция, из (6) получим:
α(h)= α0 . Так как тангенс – непрерывная функция, из (6) получим: 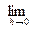
 =
= 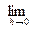 tg α(h) = tg α0., т.е.
tg α(h) = tg α0., т.е.  tg α0. Из существования производной следует дифференцируемость функции в точке х0.
tg α0. Из существования производной следует дифференцируемость функции в точке х0.
Достаточность. Доказательство существования касательной сводится к доказательству существования предела 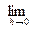 α(h).
α(h).
Пусть f дифференцируема в х0. Из (3) следует: 
 =
= 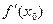 . Арктангенс – непрерывная функция, поэтому из (7) следует:
. Арктангенс – непрерывная функция, поэтому из (7) следует: 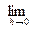 α(h) =
α(h) =  arctg
arctg  = = arctg
= = arctg 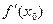 . Значит,
. Значит, 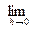 α(h) существует и равен arctg
α(h) существует и равен arctg 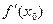 , а прямая Δ0 , проходящая через точку Мh под углом наклона к оси ОХ, равным. α0 = arctg
, а прямая Δ0 , проходящая через точку Мh под углом наклона к оси ОХ, равным. α0 = arctg 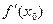 есть касательная. ◄
есть касательная. ◄
Замечание. Из равенства α0 = arctg 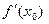 имеем: tg α0 =
имеем: tg α0 = 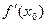 .Таким образом, производная
.Таким образом, производная 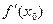 есть угловой коэффициент касательной к графику функции f в той точке М0 этого графика, абсцисса которой равна х0 – в этом состоит геометрический смысл числа
есть угловой коэффициент касательной к графику функции f в той точке М0 этого графика, абсцисса которой равна х0 – в этом состоит геометрический смысл числа 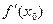 .
.
Следствие. Если существует 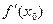 , то уравнение
, то уравнение
 где
где  , есть уравнение касательной к графику функции в точке
, есть уравнение касательной к графику функции в точке 
О приращении функкции Δ f(h)= f(x0+h) - f(x0) можно сказать, что это есть приращение ординаты точки Мh, движущейся по графику функции. Отрезок LhNh на рис. 1 равен произведению катета М0Lh на tg α0, т.е. он равен 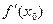 h = df(h). Это позволяет дать такую формулировку геометрического смысла дифференциала: геометрически df(h) есть приращение ординаты точки Nh, движущейся по касательной Δ0 .
h = df(h). Это позволяет дать такую формулировку геометрического смысла дифференциала: геометрически df(h) есть приращение ординаты точки Nh, движущейся по касательной Δ0 .
1.6. Односторонние производные. Бесконечные производные.
Пусть f определена на полуоткрытом промежутке 
Определение 1. Если существует предел  , то это число называют односторонней производной слева функции f в точке
, то это число называют односторонней производной слева функции f в точке 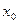 и обозначают символом
и обозначают символом 
Пусть f определена на полуоткрытом промежутке