; Þ 
(29)
Сравнивая (28) и (29), получим
(30)
Дифференциальное уравнение (30) является одномерным волновым уравнением, в котором u - фазовая скорость. Таким образом,
В стандартной записи волнового уравнениякоэффициент при второй производной по времени – величина обратная квадрату скорости распространения волны.
Упругая волна в тонком стержне. Это простейший пример распространения волн в упругой среде. При малых продольных деформациях имеет место закон Гука: 
, где s - напряжение (Н/м 2), относительная деформация 
, Е – модуль Юнга (Па). Рассмотрим элемент стержня D х в момент, когда он оказался в растянутом состоянии. По второму закону Ньютона для этого элемента
r D xS × 
= F (x +D x)+ F (x), (31)
где r - плотность, S – площадь поперечного сечения стержня. Справа стоит алгебраическая сумма сил, действующих на выделенный элемент. Так как элемент находится в растянутом состоянии, то F (x +D x) >0, F (x)<0, поэтому
F (x +D x)+ F (x)= Ss (x +D x) - Ss (x)= 
, (32)
где учтено, что сила и напряжение слева от D х имеют разные знаки (см. рис.11)! Это связано с тем, что в законе Гука s и e должны иметь знаки одинаковые, а у нас – растяжение, Þ e >0, Þ s >0! Подставим (32) в (31) и сократим на S D x; подставим 
из закона Гука и получим
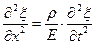, (33)
т.е. волновое уравнение, Þ коэффициент при 
позволяет выразить фазовую скорость упругой продольной волны:
(34)
В упругой среде можно возбудить и поперечные волны, тогда скорость будет выражаться через модуль сдвига G среды 
.
Упругая волна в гибком шнуре. Рассмотрим малые поперечные колебания шнура. Пусть на малый элемент шнура (рис.12) слева и справа действуют силы Fл и Fпр. Вертикальные проекции этих сил равны: слева 
; справа 
, т.к. при малых поперечных колебаниях угол α мал. Алгебраическая сумма этих сил ≈ дифференциалу выражения 
, т.е. 
≈ 
. Введем линейную плотность шнура (масса единицы длины) l, тогда второй закон Ньютона для выделенного элемента струны будет иметь вид ldx × = F 
dx, или
. (35)
Это вновь волновое уравнение, где множитель при второй производной от смещения по времени определяет фазовую скорость волны
(36)
Упругая волна в жидкостях и газах. Вывод волнового уравнения (33), полученного для тонкого стержня, можно повторить для жидкости или газа, выделив мысленно в этих средах тонкий цилиндрический канал в направлении распространения плоской волны. Необходимо только выяснить, что в этом случае играет роль модуля Юнга. При продольных волнах в среде в них возникают сжатия и разряжения отдельных слоев и закон Гука выражает связь избыточного давления с относительным изменением длины выделенного элемента 
. Причем, если D р >0,Þ давление на выделенный элемент увеличивается, Þ он сжимается, Þ D x <0, т.е. приращения давления D р и длины D x противоположны по знаку:
.
Умножив числитель и знаменатель в правой части на площадь поперечного сечения канала, получим
, Þ 
, Þ 
. (37)
Поскольку масса выделенного элемента не меняется, Þ rV =const, (r - плотность) Þ dr×V+r×dV= 0, или dr/r =- dV/V. Тогда 
, что после подстановки в (34) позволяет получить выражение для скорости продольных волн в жидкой или газовой среде 
. (38)
В частности, в газе процесс распространения звуковых волн (упругие продольные волны в звуковом диапазоне частот) можно считать адиабатическим: pV g=const. Дифференциал логарифма этого выражения равен нулю: 
, Þ 
® (37), Þ 
, Þ скорость звуковой волны в газе равна 
, что с учетом уравнения Менделеева-Клапейрона можно
преобразовать к виду 
. Последняя формула является менее общей по сравнению с (38), однако очень удобна для оценки скорости звука в различных газах. (Кто-то еще помнит, что 
и называется показателем адиабаты? Не побоюсь спросить: а что такое i?)
Энергия упругой волны. К закрепленной с одного конца струне (стержню) приложим с другой стороны растягивающую силу, которая по закону Гука в пределах упругой деформации должна изменяться пропорционально смещению: F=mx, где m - коэффициент упругости. Для нахождения работы этой силы необходимо проинтегрировать выражение Fdx=mxdx в пределах от 0 до х. Поэтому работа равна А = 
. Эта работа идет на увеличение упругой энергии стержня, Þ потенциальная энергия растянутого на х стержня (струны) равна
U = . (40)
