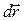Силы, с которыми две материальные точки действуют друг на друга, всегда равны по модулю и направлены в противоположные стороны вдоль прямой, соединяющей эти точки:
 (21)
(21)
Таким образом, обе силы равны по модулю одновременно. Это соответствует представлению о мгновенном распространении взаимодействий – принцип дальнодействия ньютоновской механики. Следовательно, взаимодействие распространяется с бесконечно большой скоростью: изменение состояния тела мгновенно обнаружится во всех взаимодействующих с ним телах, как бы далеко они не находились.
Законы Ньютона являются основными законами механики. В соответствии с принципом относительности Галилея, во всех инерциальных системах все законы механики одинаковы. Действительно, масса материальной точки и её ускорение одинаковы во всех инерциальных системах отсчета. Сила – тоже, поскольку она определяется только относительным расположением тел и их относительных скоростей, которые одинаковы во всех инерциальных системах отсчета. Так как все три величины, входящие в (18) не меняются, следовательно, и само основное уравнение динамики остается неизменным, иными словами, инвариантным относительно преобразований Галилея. Рассмотрим наиболее часто встречающиеся силы. Гравитационное притяжение. Закон Всемирного тяготения. Сила гравитационного притяжения между двумя материальными точками пропорциональна произведению масс точек 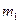 и
и 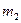 и обратно пропорциональна квадрату расстояния r между ними и направлена вдоль прямой, соединяющей эти точки:
и обратно пропорциональна квадрату расстояния r между ними и направлена вдоль прямой, соединяющей эти точки:
 , (22)
, (22)
где g - гравитационная постоянная. Массы в (22) называются гравитационными, в отличие от ранее рассмотренных инертных масс. Экспериментально установлено, что гравитационная и инертная массы любого тела строго пропорциональны друг другу. Обычно их полагают равными, для чего выбирают один и тот же эталон массы. Введенное таким образом понятие массы является и мерой инертности тела и мерой его гравитационного взаимодействия с другими телами.
З акон Кулона: Сила электростатического взаимодействия между двумя точечными зарядами пропорциональна произведению величин зарядов q 1 и q 2, обратно пропорциональна квадрату расстояния r между ними и направлена вдоль прямой, соединяющей заряды:
 . (23)
. (23)
В отличие от гравитационной, кулоновская сила может быть как силой притяжения (между разноименными зарядами), так и силой отталкивания (между одноименными зарядами). Если заряды движутся относительно друг друга, между ними возникает еще и магнитное взаимодействие, а закон (23) перестает выполняться точно. Взаимодействие между движущимися заряженными телами обладает довольно сложной топологией и называется электромагнитным.
Кулоновское и гравитационное взаимодействие лежат в основе всего разнообразия механических явлений, но не всегда разумно каждый случай сводить к этим двум фундаментальным взаимодействиям. Для упрощения часто бывает удобно использовать приближенные силы:
Однородная сила тяжести: 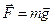 , где
, где 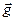 - ускорение свободного падения, которое считается постоянным вблизи поверхности Земли. Обратите внимание! В отличие от силы тяжести
- ускорение свободного падения, которое считается постоянным вблизи поверхности Земли. Обратите внимание! В отличие от силы тяжести  , вес
, вес  -это сила, с которой тело действует на опору (или подвес), неподвижную относительно тела. Если тело и его опора неподвижны относительно Земли, то вес равен силе тяжести (однако эти силы приложены к разным предметам: сила тяжести – к телу, а вес – к его опоре).
-это сила, с которой тело действует на опору (или подвес), неподвижную относительно тела. Если тело и его опора неподвижны относительно Земли, то вес равен силе тяжести (однако эти силы приложены к разным предметам: сила тяжести – к телу, а вес – к его опоре).
Упругая сила – это сила, пропорциональная смещению материальной точки из положения равновесия и направленная к положению равновесия:
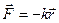 , (24)
, (24)
где 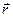 - радиус-вектор, характеризующий смещение частицы от положения равновесия,
- радиус-вектор, характеризующий смещение частицы от положения равновесия,  - коэффициент, зависящий от «упругих» свойств конкретной силы. Примером такой силы может быть сила упругой деформации при растяжении (сжатии) пружины или стержня, которая подчиняется до поры до времени закону Гука:
- коэффициент, зависящий от «упругих» свойств конкретной силы. Примером такой силы может быть сила упругой деформации при растяжении (сжатии) пружины или стержня, которая подчиняется до поры до времени закону Гука:  , где
, где  - величина упругой деформации.
- величина упругой деформации.
 Сила трения. Различают силу трения скольжения, которая в некоторых пределах пропорциональна по модулю силе давления, прижимающей трущиеся поверхности друг к другу:
Сила трения. Различают силу трения скольжения, которая в некоторых пределах пропорциональна по модулю силе давления, прижимающей трущиеся поверхности друг к другу:  , и силу трения покоя, величина которой зависит от других приложенных к телу сил. Например, если к покоящемуся телу, приложить горизонтальную силу
, и силу трения покоя, величина которой зависит от других приложенных к телу сил. Например, если к покоящемуся телу, приложить горизонтальную силу  , которая увеличивается от нуля, то сначала тело будет продолжать покоиться, а начиная с некоторого её значения тело начнет двигаться. Пока тело покоится, векторная сумма всех приложенных сил обязана быть равной нулю, поэтому сила трения покоя направлена противоположно
, которая увеличивается от нуля, то сначала тело будет продолжать покоиться, а начиная с некоторого её значения тело начнет двигаться. Пока тело покоится, векторная сумма всех приложенных сил обязана быть равной нулю, поэтому сила трения покоя направлена противоположно  и равна ей по модулю; следовательно, сила трения покоя будет возрастать до момента, пока тело не начнет двигаться. Далее характер силы трения меняется, т.к. она становится силой трения скольжения
и равна ей по модулю; следовательно, сила трения покоя будет возрастать до момента, пока тело не начнет двигаться. Далее характер силы трения меняется, т.к. она становится силой трения скольжения  , т.е. постоянной, если постоянна сила
, т.е. постоянной, если постоянна сила 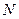 (рис.6). Наклонный участок соответствует силе трения покоя, а горизонтальный – силе трения скольжения.
(рис.6). Наклонный участок соответствует силе трения покоя, а горизонтальный – силе трения скольжения.
Сила сопротивления. Обычно так называют силу типа трения, но которая возникает в жидкости или газе. Эта сила зависит от скорости:  , часто и более сложным образом.
, часто и более сложным образом.
В заключение следует сказать, что второй закон Ньютона является основным расчетным законом динамики, поэтому его часто называют основным уравнением динамики материальной точки, или уравнением движения в векторном виде.
О законах сохранения. Любое тело или совокупность тел можно рассмотреть, как систему материальных точек. Состояние системы характеризуется одновременным заданием координат и скоростей всех этих точек. В принципе, с помощью уравнений движения для всех точек можно решить любую механическую задачу. Однако из-за возрастания количества этих уравнений по мере усложнения системы зачастую довести решение до конца оказывается практически невозможным. Кроме того, часто бывает, что законы действия некоторых сил неизвестны, и тогда такой подход становится принципиально невозможным. Обойти подобные трудности во многих случаях позволяют законы сохранения. Хотя состояние системы со временем может меняться достаточно сложным способом, существуют такие величины, которые обладают замечательным свойством сохраняться во времени. Среди таких сохраняющихся величин наиболее важную роль играют энергия, импульс и момент импульса.
Законы сохранения энергии, импульса и момента импульса связаны, как выяснилось к настоящему времени, с фундаментальными свойствами времени и пространства – однородностью и изотропностью. А именно: закон сохранения энергии связан с однородностью времени; закон сохранения импульса – с однородностью пространства; закон сохранения момента импульса связан с изотропностью пространства. Роль законов сохранения особенно возросла, после того, как выяснилось, что они далеко выходят за рамки механики и представляют собой универсальные законы природы.
Закон сохранения импульса. По определению, импульс частицы 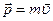 . Согласно основному уравнению (19) динамики (второму закону Ньютона)
. Согласно основному уравнению (19) динамики (второму закону Ньютона) 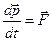 . Если
. Если  =0, то
=0, то  = const. Уравнение (19) позволяет найти приращение импульса, если известна зависимость силы от времени. Действительно, из (19) Þ
= const. Уравнение (19) позволяет найти приращение импульса, если известна зависимость силы от времени. Действительно, из (19) Þ 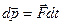 . Поскольку известен вид функции
. Поскольку известен вид функции 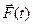 , можно это выражение проинтегрировать:
, можно это выражение проинтегрировать:
 . (25)
. (25)
В частности, если  = const, то этот вектор можно вынести из-под знака интеграла, и тогда
= const, то этот вектор можно вынести из-под знака интеграла, и тогда
 .
.
Пусть теперь имеется произвольная система частиц. Силы (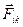 ) взаимодействия между частицами системы называются внутренними, а силы (
) взаимодействия между частицами системы называются внутренними, а силы (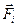 ) взаимодействия частиц системы с телами, не входящими в систему, - внешними. Определим импульс системы как векторную сумму импульсов
) взаимодействия частиц системы с телами, не входящими в систему, - внешними. Определим импульс системы как векторную сумму импульсов 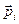 (импульс i -й частицы) всех её частиц:
(импульс i -й частицы) всех её частиц: 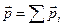 . Продифференцируем это выражение по времени:
. Продифференцируем это выражение по времени:  . Запишем для каждой частицы
. Запишем для каждой частицы 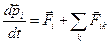 и подставим в предыдущее уравнение:
и подставим в предыдущее уравнение: 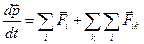 , где двойная сумма – это сумма всех внутренних сил, которая равна нулю, потому, что в ней каждая пара сил,
, где двойная сумма – это сумма всех внутренних сил, которая равна нулю, потому, что в ней каждая пара сил, 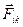 = -
= - 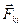 по третьему закону Ньютона; иначе говоря, силы взаимодействия между частицами внутри системы попарно одинаковы по модулю и противоположено направлены. Поэтому результирующая каждой пары равна нулю, а значит, равна нулю и сумма этих нулей:
по третьему закону Ньютона; иначе говоря, силы взаимодействия между частицами внутри системы попарно одинаковы по модулю и противоположено направлены. Поэтому результирующая каждой пары равна нулю, а значит, равна нулю и сумма этих нулей: 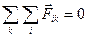 . Остается только сумма внешних сил
. Остается только сумма внешних сил  , поэтому
, поэтому
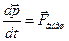 . (26)
. (26)
Отсюда 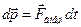 , что после интегрирования дает
, что после интегрирования дает
 . (27)
. (27)
Т.е. приращение импульса системы равно импульсу всех результирующих сил за промежуток времени t. Выражения (26,27) описывают изменение импульса системы материальных точек.
Система называется замкнутой (изолированной), если на неё не действуют внешние силы.
Согласно (26) импульс системы может измениться только под действием внешних сил. Отсюда вытекает закон сохранения импульса: Импульс изолированной системы частиц остается постоянным:
 . (28)
. (28)
Следствия. 1 Импульс может сохраняться и у незамкнутой системы, если сумма всех внешних сил равна нулю, что непосредственно следует из (26 и 27). 2 У незамкнутой системы может сохраняться не сам импульс, а его проекция 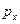 на некоторое направление х. Это бывает тогда, когда проекция результирующей внешней силы на это направление равна нулю, т.е. вектор
на некоторое направление х. Это бывает тогда, когда проекция результирующей внешней силы на это направление равна нулю, т.е. вектор 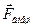 перпендикулярен направлению х. Действительно, спроектировав уравнение (26) на направление х, получим
перпендикулярен направлению х. Действительно, спроектировав уравнение (26) на направление х, получим 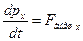 , откуда следует, что если правая часть равна нулю, то равна нулю и производная слева, Þ р х= const. Например, сохраняется проекция импульса системы на горизонтальное направление, если система находится в однородном поле сил тяготения.
, откуда следует, что если правая часть равна нулю, то равна нулю и производная слева, Þ р х= const. Например, сохраняется проекция импульса системы на горизонтальное направление, если система находится в однородном поле сил тяготения.
Центр масс. Назовем центром масс системы частиц точку с радиусом-вектором
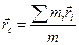 , (30)
, (30)
где m – сумма масс частиц системы, 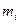 и
и  соответственно масса и радиус-вектор i -й частицы. Центр масс обладает замечательным свойством, которое мы обнаружим, продифференцировав (30), чтобы найти скорость:
соответственно масса и радиус-вектор i -й частицы. Центр масс обладает замечательным свойством, которое мы обнаружим, продифференцировав (30), чтобы найти скорость: 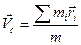 . Поскольку в числителе дроби стоит импульс системы, то его легко выразить через скорость центра масс:
. Поскольку в числителе дроби стоит импульс системы, то его легко выразить через скорость центра масс:
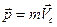 . (31)
. (31)
Таким образом, импульс системы равен произведению массы системы на скорость её центра масс. Очевидно, если скорость центра масс равна нулю, то система в целом покоится, какие бы перемещения внутри неё не происходили. Введение скорости центра масс 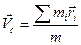 , позволяет придать компактную форму уравнению (26):
, позволяет придать компактную форму уравнению (26):
 , (32)
, (32)
которое является уравнением движения центра масс – по форме вторым законом Ньютона. Откуда видно, что центр масс системы частиц движется так, как если бы вся масса системы была сосредоточена в этом центре, и к ней была бы приложена результирующая всех внешних сил. Если центр масс системы движется равномерно и прямолинейно, значит. импульс системы сохраняется в процессе движения.
Закон сохранения энергии.
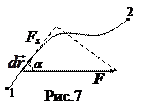 Работа и мощность. Пусть частица под действием силы
Работа и мощность. Пусть частица под действием силы  совершает перемещение по некоторой траектории 1®2 (рис.7). По определению, элементарной работой силы
совершает перемещение по некоторой траектории 1®2 (рис.7). По определению, элементарной работой силы  при перемещении
при перемещении 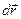 называется скалярное произведение этих величин:
называется скалярное произведение этих величин:
 , (33)
, (33)
 где
где 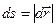 - элементарный путь, F s – проекция силы на касательное направление (на вектор
- элементарный путь, F s – проекция силы на касательное направление (на вектор 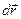 ). Величина δА – скаляр, в частности равный нулю, если
). Величина δА – скаляр, в частности равный нулю, если  ^
^ 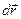 . таким образом, сила, перпендикулярная перемещению, работы не совершает. Интегрируя выражение (33) по всем элементарным участкам траектории от точки 1 до точки 2, находим работу на всем пути 1®2:
. таким образом, сила, перпендикулярная перемещению, работы не совершает. Интегрируя выражение (33) по всем элементарным участкам траектории от точки 1 до точки 2, находим работу на всем пути 1®2:
|
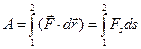 . (34)
. (34)
Работа упругой силы. Пусть частица В перемещается по некоторой траектории 1®2 (рис.8) и на неё действует сила 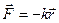 , где
, где 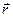 - радиус-вектор частицы В относительно некоторой точки О. Элементарная работа при перемещении
- радиус-вектор частицы В относительно некоторой точки О. Элементарная работа при перемещении 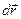 равна
равна 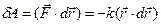 . Из рисунка очевидно, что
. Из рисунка очевидно, что  , где dr – приращение модуля радиус-вектора, Þ
, где dr – приращение модуля радиус-вектора, Þ  . Чтобы убедиться в правильности последнего преобразования, прочитайте его справа налево. Для вычисления работы на всем пути осталось только проинтегрировать:
. Чтобы убедиться в правильности последнего преобразования, прочитайте его справа налево. Для вычисления работы на всем пути осталось только проинтегрировать:
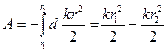 . (35)
. (35)
 Работа гравитационной (кулоновской) силы. Мы воспользуемся опять рис.8, но слова будут другие,- будьте внимательны! Пусть в точке О находится неподвижный силовой центр – материальная точка, действующая на частицу В с силой
Работа гравитационной (кулоновской) силы. Мы воспользуемся опять рис.8, но слова будут другие,- будьте внимательны! Пусть в точке О находится неподвижный силовой центр – материальная точка, действующая на частицу В с силой  , которая может быть представлена в виде
, которая может быть представлена в виде  =
= 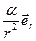 , где a - равна (- gm 1 m 2 – для гравитационного; kq 1 q 2 - для кулоновского взаимодействий). Единичный вектор (орт)
, где a - равна (- gm 1 m 2 – для гравитационного; kq 1 q 2 - для кулоновского взаимодействий). Единичный вектор (орт)  направлен также, как
направлен также, как 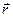 (он не изображен на рисунке). Элементарная работа этой силы равна
(он не изображен на рисунке). Элементарная работа этой силы равна 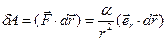 , где последнее скалярное произведение равно dr. Поэтому
, где последнее скалярное произведение равно dr. Поэтому  , в чем легко убедиться, если прочесть последнее равенство справа на лево. Осталось проинтегрировать, и тогда работа на всем пути 1®2 равна
, в чем легко убедиться, если прочесть последнее равенство справа на лево. Осталось проинтегрировать, и тогда работа на всем пути 1®2 равна
 . (36)
. (36)
Работа однородной силы тяжести. Запишем эту силу через орт  - единичный вектор направленный вертикально вверх:
- единичный вектор направленный вертикально вверх:  . Элементарная работа силы тяжести на перемещении
. Элементарная работа силы тяжести на перемещении 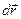 равна
равна
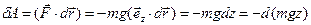 .
.
Работа этой силы на всем пути равна 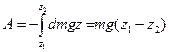 (37)
(37)
Обратите внимание! Во всех рассмотренных случаях величина работы зависела только от координат начальной и конечной точек траектории. Не все силы обладают таким свойством, например, работа силы трения от формы траектории зависит. Единицей работы в СИ является джоуль (Дж).
Мощность – это работа, совершаемая силой в единицу времени. Если за время dt сила  совершает работу
совершает работу  , то мощность Р =
, то мощность Р =  . Итак,
. Итак,
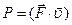 . (38)
. (38)

 Очевидно, чтобы найти работу, зная мощность, достаточно проинтегрировать
Очевидно, чтобы найти работу, зная мощность, достаточно проинтегрировать
 . (39)
. (39)
Единицей мощности в СИ является ватт (Вт), равный 1 Дж/с.
Консервативные силы. Если в каждой точке пространства на помещенную туда частицу действует сила, то говорят, что частица помещена в поле сил. Если поле не меняется со временем, то оно называется стационарным. Некоторые стационарные поля обладают важным свойством: Забота сил поля, совершаемая его силами при перемещении частицы между любыми точками поля 1 и 2 зависит только от координат (или радиусов-векторов) этих точек 1 и 2. Силы, обладающие таким свойством называются консервативными, а их поля потенциальными. Эквивалентная формулировка этого свойства гласит: поле является потенциальным, если работа его сил на любом замкнутом пути равна нулю. Чтобы убедиться в этом, разобьём произвольный замкнутый контур на две части: 1 а 2 и 2 b 1 (рис.10). Тогда работа на замкнутом пути равна А = А 1а2 + А 2 b 1. Поскольку А 1а2 = - А 2 b 1, так как каждая из этих работ зависит только от координат точек 1 и 2, а при изменении порядка точек меняется и знак работы, то А = 0.
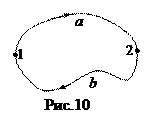 К числу неконсервативных сил относятся силы трения и сопротивления.
К числу неконсервативных сил относятся силы трения и сопротивления.
 Поле центральных сил. Силы, зависящие только от расстояния между частицами, и направленные вдоль прямой, соединяющие эти частицы, называются центральными. Примерами центральных полей являются кулоновские, гравитационные и упругие. Центральную силу, действующую на частицу М со стороны частицы О, можно представить в виде
Поле центральных сил. Силы, зависящие только от расстояния между частицами, и направленные вдоль прямой, соединяющие эти частицы, называются центральными. Примерами центральных полей являются кулоновские, гравитационные и упругие. Центральную силу, действующую на частицу М со стороны частицы О, можно представить в виде
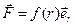 ,
,
где 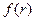 - функция, зависящая только от расстояния r между частицами (рис.11). Докажем, что центральные силы являются консервативными. Элементарная работа центральной силы
- функция, зависящая только от расстояния r между частицами (рис.11). Докажем, что центральные силы являются консервативными. Элементарная работа центральной силы  на перемещении
на перемещении 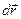 равна
равна  . Так как
. Так как  = dr, то
= dr, то 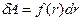 . Работа этой силы на произвольном пути между точками 1 и 2 траектории равна
. Работа этой силы на произвольном пути между точками 1 и 2 траектории равна
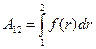 .
.
Полученное выражение не зависит от траектории, а зависит только от вида функции 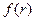 и значений радиус-векторов
и значений радиус-векторов  и
и  начальной и конечной точек траектории. Обобщим: пусть на частицу М действует не одна сила
начальной и конечной точек траектории. Обобщим: пусть на частицу М действует не одна сила  со стороны точки О, а несколько сил
со стороны точки О, а несколько сил  , действующих со стороны системы материальных точек, причем каждая из этих сил является центральной. Тогда работа результирующей силы при перемещении частицы М из 1 в 2 равна алгебраической сумме работ отдельных сил. А так как работа каждой силы не зависит от траектории, то и работа результирующей силы также не зависит от пути.
, действующих со стороны системы материальных точек, причем каждая из этих сил является центральной. Тогда работа результирующей силы при перемещении частицы М из 1 в 2 равна алгебраической сумме работ отдельных сил. А так как работа каждой силы не зависит от траектории, то и работа результирующей силы также не зависит от пути.
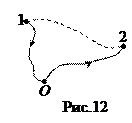 Потенциальная энергия частицы в поле. То обстоятельство, что работа консервативных сил зависит только от начального и конечного положений частицы, дает возможность ввести понятие потенциальной энергии. Пусть в поле консервативных сил мы перемещаем (мысленно) из разных точек Пi поля частицу в одну и ту же фиксированную точку О и каждый раз вычисляем соответствующую работу сил поля. Поскольку работа сил такого поля в принципе может зависеть только от координат начальной и конечной точек Пi и О, причем при фиксированной точке О меняются только координаты точек Пi, то в итоге эта работа AПО будет функцией только координат (радиус-вектора) точки П. Обозначим эту функцию U (
Потенциальная энергия частицы в поле. То обстоятельство, что работа консервативных сил зависит только от начального и конечного положений частицы, дает возможность ввести понятие потенциальной энергии. Пусть в поле консервативных сил мы перемещаем (мысленно) из разных точек Пi поля частицу в одну и ту же фиксированную точку О и каждый раз вычисляем соответствующую работу сил поля. Поскольку работа сил такого поля в принципе может зависеть только от координат начальной и конечной точек Пi и О, причем при фиксированной точке О меняются только координаты точек Пi, то в итоге эта работа AПО будет функцией только координат (радиус-вектора) точки П. Обозначим эту функцию U (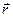 ), Þ
), Þ
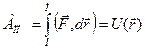 . (40)
. (40)
Функция U (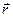 ) называется потенциальной энергией. Найдем работу А 12 сил поля при перемещении частицы из точки 1 в точку 2 (пунктир на рис.12). Поскольку поле консервативно, то эта работа не зависит от того, по какой траектории мы перемещаем частицу из 1 в 2 – по пунктирной линии, или через точку О (т.е. по пути 1®О®2), Þ
) называется потенциальной энергией. Найдем работу А 12 сил поля при перемещении частицы из точки 1 в точку 2 (пунктир на рис.12). Поскольку поле консервативно, то эта работа не зависит от того, по какой траектории мы перемещаем частицу из 1 в 2 – по пунктирной линии, или через точку О (т.е. по пути 1®О®2), Þ
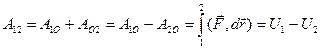 . (41)
. (41)
Выражение справа – это убыль потенциальной энергии. Потому, что прибыль (т.е. приращение – это 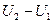 ). Таким образом,
). Таким образом,
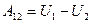 , Þ
, Þ
работа сил поля на пути 1®2 равна убыли потенциальной энергии частицы в этом поле. Очевидно, что работа сил поля определяет лишь разность потенциальных энергий, но не их абсолютное значение, Þ потенциальная энергия определена (как первообразная!) с точностью до произвольной постоянной. И наоборот, если нам удалось представить работу как убыль некоторой функции координат, то эта функция и есть потенциальная энергия. Но мы недавно вычисляли эту работу для полей упругой и гравитационной (кулоновской) сил и получили во всех случаях разность значений соответствующей функции (см. формулы 35-37), из чего немедленно следует, что потенциальная энергия в данных силовых полях имеет вид: 1 в поле упругой силы U (r) =  +const;
+const;
2 в гравитационном (кулоновском) поле U (r)= 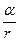 +const;
+const;
3 в однородном поле сил тяжести U (z) = 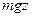 + const.
+ const.
Как следует из (41),  = - dU, Þ Fdr cos a = - dU, Þ
= - dU, Þ Fdr cos a = - dU, Þ 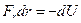 , Þ
, Þ  . Поскольку dr – это модуль малого перемещения вдоль траектории, Fr – это проекция силы на направление этого перемещения, т.е. на любое направление, вдоль которого нам вздумалось перемещаться, то удобнее эту мысль переформулировать так: проекция силы на произвольное направление х в потенциальном поле равна минус производной от потенциальной энергии по координате:
. Поскольку dr – это модуль малого перемещения вдоль траектории, Fr – это проекция силы на направление этого перемещения, т.е. на любое направление, вдоль которого нам вздумалось перемещаться, то удобнее эту мысль переформулировать так: проекция силы на произвольное направление х в потенциальном поле равна минус производной от потенциальной энергии по координате: