Кинематика
 Кинематика точки. Существуют три способа описания движения материальной точки: векторный координатный и ²естественный². В векторном способе положение некоторой точки А задают радиус-вектором
Кинематика точки. Существуют три способа описания движения материальной точки: векторный координатный и ²естественный². В векторном способе положение некоторой точки А задают радиус-вектором 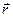 (x,y,z,t), проведенном из начала системы отсчета в точку А. Во время движения конец радиус-вектора описывает в пространстве кривую, которая называется траекторией.
(x,y,z,t), проведенном из начала системы отсчета в точку А. Во время движения конец радиус-вектора описывает в пространстве кривую, которая называется траекторией.
Скорость. Пусть за время Δ t точка А переместилась из точки 1 в точку 2 (рис.1). Вектор  , идущий из 1 в 2, называется перемещением:
, идущий из 1 в 2, называется перемещением:  =
= 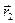 -
-  . Средним вектором скорости называется вектор
. Средним вектором скорости называется вектор  . Очевидно направление
. Очевидно направление  совпадает с направлением вектора перемещения! Однако вектор мгновенной скорости будет направлен по касательной к траектории. Поэтому скорость определим как предел среднего вектора скорости при Δ t →0:
совпадает с направлением вектора перемещения! Однако вектор мгновенной скорости будет направлен по касательной к траектории. Поэтому скорость определим как предел среднего вектора скорости при Δ t →0:
 . (1)
. (1)
Выражение в правой части - это производная. Поэтому можно дать более лаконичное определение скорости: скорость – это производная от радиуса-вектора по времени.
Ускорение – это скорость изменения скорости, т.е. производная от скорости по времени:
 (2)
(2)
Из данных определений следует, что, зная зависимость радиус-вектора от времени 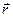 (t), можно найти скорость и ускорение точки в любой момент.
(t), можно найти скорость и ускорение точки в любой момент.
Обратная задача. Можно ли найти  (t) и/или
(t) и/или 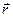 (t), зная зависимость
(t), зная зависимость  ? Оказывается для однозначного решения этой задачи недостаточно одной зависимости
? Оказывается для однозначного решения этой задачи недостаточно одной зависимости  , необходимо еще задать начальные условия: например, скорость
, необходимо еще задать начальные условия: например, скорость 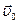 и радиус вектор
и радиус вектор  точки в некоторый начальный момент времени t =0. Рассмотрим простейший пример. Пусть
точки в некоторый начальный момент времени t =0. Рассмотрим простейший пример. Пусть  . Из (2) Þ
. Из (2) Þ 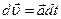 Þ
Þ  . Но
. Но  - это изменение скорости, а не сама скорость:
- это изменение скорости, а не сама скорость:  =
=  . Поэтому, чтобы найти
. Поэтому, чтобы найти  необходимо знать
необходимо знать 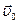 в начальный момент времени:
в начальный момент времени:  , Þ
, Þ
 (3)
(3)
Аналогично для 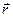 :
:  , где
, где  =
=  -
-  . Для нахождения самого радиуса-вектора
. Для нахождения самого радиуса-вектора 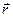 необходимо знать его значение в начальный момент времени
необходимо знать его значение в начальный момент времени  :
:
 . (4)
. (4)
Обратите внимание! Чтобы найти 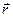 по зависимости
по зависимости  (t) было необходимо один раз проинтегрировать и дополнительно знать одно начальное условие. Чтобы найти
(t) было необходимо один раз проинтегрировать и дополнительно знать одно начальное условие. Чтобы найти 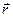 по зависимости
по зависимости  потребовалось два раза проинтегрировать и два начальных условия. Так и должно быть, поскольку интеграл определен с точностью до константы. И еще: в данном примере мы вынесли ускорение из-под интеграла, потому что
потребовалось два раза проинтегрировать и два начальных условия. Так и должно быть, поскольку интеграл определен с точностью до константы. И еще: в данном примере мы вынесли ускорение из-под интеграла, потому что  . Если это не так, то выносить нельзя! Сравните: при интегрировании скорости, мы ее не выносили, т.к. скорость оказалась функцией времени.
. Если это не так, то выносить нельзя! Сравните: при интегрировании скорости, мы ее не выносили, т.к. скорость оказалась функцией времени.
При использовании координатного способа некоторое векторное уравнение проектируют на оси координат. Каждому векторному уравнению соответствуют три скалярных в проекциях на оси x,y,z (в декартовых координатах). Со скалярными уравнениями обращаться проще, но их в три раза больше, поэтому сначала следует записывать уравнения в векторном виде. Так виден физический смысл векторных величин. Зависимости 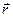 (x,y,z,t) соответствуют три скалярных уравнения: x (t), y (t), z (t). Определению вектора скорости (1) соответствуют ux (t), u y (t), u z (t):
(x,y,z,t) соответствуют три скалярных уравнения: x (t), y (t), z (t). Определению вектора скорости (1) соответствуют ux (t), u y (t), u z (t):
 ;
;  ;
;  ; аналогично для ускорения:
; аналогично для ускорения: 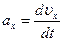 ;
;  ;
;  .
.
 Зная три проекции векторов скорости и ускорения можно найти и модули этих величин в любой момент времени, например, модуль вектора скорости
Зная три проекции векторов скорости и ускорения можно найти и модули этих величин в любой момент времени, например, модуль вектора скорости  . Если вектор скорости составляет с осью х угол a, то ux = u cosa; u y = u sina; и т.д… (рис.2) Аналогично определяются модули векторов
. Если вектор скорости составляет с осью х угол a, то ux = u cosa; u y = u sina; и т.д… (рис.2) Аналогично определяются модули векторов 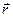 и
и 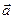 :
:
 ;
;  . Почему-то формула для модуля для вектора
. Почему-то формула для модуля для вектора 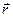 осознается студентами с большим трудом, хотя для этого достаточно знать откуда начинается радиус-вектор и теорему Пифагора.
осознается студентами с большим трудом, хотя для этого достаточно знать откуда начинается радиус-вектор и теорему Пифагора.
Решение обратной задачи – нахождение скорости и закона движения точки по заданному ускорению – производится, как и в векторном способе, путем интегрирования с начальными условиями. (Помните, что количество интегрирований и начальных условий должно совпадать?)
Естественный способ выгодно использовать, когда траектория известна. Тогда положение точки А определяют дуговой координатой l (или путем S), отсчитанной от выбранного на траектории начала: при этом произвольно назначают одно направление вдоль траектории положительным, а другое – отрицательным. Введем единичный вектор  , направленный по касательной к траектории в в положительную сторону. Это направление называется тангенциальным. Поскольку вектор скорости направлен также, скорость можно записать как
, направленный по касательной к траектории в в положительную сторону. Это направление называется тангенциальным. Поскольку вектор скорости направлен также, скорость можно записать как
 , (5)
, (5)
где 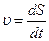 . Очевидно,
. Очевидно,  .
.
Продифференцировав (5) по времени, найдем ускорение:
 ; (6)
; (6)
затем преобразуем второе слагаемое:
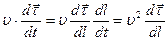 . (7)
. (7)
 Определим приращение вектора
Определим приращение вектора 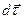 на участке dl (рис.3). Поскольку dl мало, всегда можно найти такую окружность радиуса
на участке dl (рис.3). Поскольку dl мало, всегда можно найти такую окружность радиуса 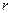 с центром в точке О, что ее дуга будет на участке dl совпадать с элементом траектории. Тогда точка О будет называться центром кривизны траектории в этом месте, а
с центром в точке О, что ее дуга будет на участке dl совпадать с элементом траектории. Тогда точка О будет называться центром кривизны траектории в этом месте, а 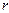 - радиусом кривизны. Векторы
- радиусом кривизны. Векторы  и
и  , как касательные перпендикулярны радиусам в точках касания, Þ угол между ними также как и между этими радиусами равен da, что видно на рис.3 справа, где оба вектора отложены от одной точки. Угол da можно выразить двумя способами: da =
, как касательные перпендикулярны радиусам в точках касания, Þ угол между ними также как и между этими радиусами равен da, что видно на рис.3 справа, где оба вектора отложены от одной точки. Угол da можно выразить двумя способами: da =  и da =
и da = 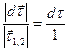 , так как векторы
, так как векторы  и
и  - векторы единичной длины. Приравнивая правые части, находим
- векторы единичной длины. Приравнивая правые части, находим  . Поскольку вектор
. Поскольку вектор 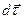 перпендикулярен векторам
перпендикулярен векторам  и
и  (из-за неограниченной малости dl), и направлен к центру кривизны О, то последнее равенство можно записать с помощью единичного вектора
(из-за неограниченной малости dl), и направлен к центру кривизны О, то последнее равенство можно записать с помощью единичного вектора 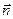 (направлен вдоль
(направлен вдоль 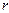 к центру О):
к центру О):  . Подставляя этот результат в (7)®(6), найдем окончательное выражение для ускорения в естественных координатах:
. Подставляя этот результат в (7)®(6), найдем окончательное выражение для ускорения в естественных координатах:
 (8)
(8)
В (8) первое слагаемое называют тангенциальным ускорением, а второе нормальным:
 , Þ проекция тангенциального ускорения
, Þ проекция тангенциального ускорения  и характеризует скорость изменения скорости по величине;
и характеризует скорость изменения скорости по величине;  , Þ величина нормального ускорения
, Þ величина нормального ускорения  и характеризует скорость изменения скорости по направлению. Модуль полного ускорения точки
и характеризует скорость изменения скорости по направлению. Модуль полного ускорения точки  .
.
Кинематика твердого тела.
Твердым называется тело, у которого расстояния между любыми его точками сохраняются. Иначе говоря, твердое тело никак не деформируется при любых его движениях. Основными видами движения твердого тела являются поступательное, вращение вокруг неподвижной оси, плоское движение.
Поступательным движением твердого тела называется такое его движение, при котором любая прямая, связанная с телом, остается параллельной своему начальному положению. Поэтому все точки тела движутся по одинаковым траекториям и их скорости и ускорения в любой момент времени одинаковы. Описание поступательного движения твердого тела сводится к описанию любой его точки, и поэтому не требует отдельного рассмотрения.
 Вращение вокруг неподвижной оси. При таком вращении все точки твердого тела описывают окружности разных радиусов. Пусть твердое тело поворачивается за время dt вокруг неподвижной оси ОО¢ на угол dφ (рис.4). Этот поворот мы будем характеризовать вектором углового перемещения
Вращение вокруг неподвижной оси. При таком вращении все точки твердого тела описывают окружности разных радиусов. Пусть твердое тело поворачивается за время dt вокруг неподвижной оси ОО¢ на угол dφ (рис.4). Этот поворот мы будем характеризовать вектором углового перемещения  , направление которого совпадает с осью ОО¢ и связано с вектором перемещения
, направление которого совпадает с осью ОО¢ и связано с вектором перемещения 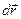 по правилу правого винта (если поворачивать винт в сторону
по правилу правого винта (если поворачивать винт в сторону 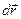 , то он должен ввинчиваться в направлении
, то он должен ввинчиваться в направлении  , например, в нашем случае вверх). Из рисунка 4 видно, что
, например, в нашем случае вверх). Из рисунка 4 видно, что 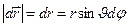 , или в векторном виде
, или в векторном виде
 . (9)
. (9)
Введенный таким образом вектор углового перемещения производит какое-то неестественное впечатление – он таким и является. Приписать этому объекту направление по определению (такие векторы называются аксиальными) удобно, т.к. убедиться, что векторы угловых перемещений удовлетворяют всем правилам действий с векторами: сложению, умножению на число, скалярному и векторному умножению и т.д. – совсем не трудно, убедитесь в этом самостоятельно.
Угловая скорость и угловое ускорение. Угловой скоростью называется аксиальный вектор  . Очевидно, он направлен также как вектор
. Очевидно, он направлен также как вектор  .
.
Угловым ускорением называется также аксиальный вектор  . Направление вектора
. Направление вектора  совпадает с вектором
совпадает с вектором  , если угловая скорость увеличивается, и противоположно вектору
, если угловая скорость увеличивается, и противоположно вектору  , если угловая скорость убывает.
, если угловая скорость убывает.
Связь между линейными и угловыми величинами. Выберем произвольную точку А твердого тела и выясним, как связаны ее линейная (обычная) скорость и угловая скорость (рис.4). Разделим выражение (9) на dt:  . Таким образом, угловая скорость
. Таким образом, угловая скорость  и линейная скорость
и линейная скорость  связаны посредством векторного произведения
связаны посредством векторного произведения
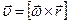 . (10)
. (10)
Модуль вектора скорости u=ω 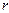 sin J =ωρ, где ρ – радиус окружности, по которой движется точка А твердого тела. Продифференцировав (10) по времени, найдем полное ускорение точки А:
sin J =ωρ, где ρ – радиус окружности, по которой движется точка А твердого тела. Продифференцировав (10) по времени, найдем полное ускорение точки А:
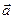 =
=  , или
, или 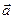 =
=  (11)
(11)
Так как векторы  и
и  направлены вдоль оси вращения, первое слагаемое в (11) представляет собой тангенциальное ускорение
направлены вдоль оси вращения, первое слагаемое в (11) представляет собой тангенциальное ускорение  =
=  , а второе - нормальное
, а второе - нормальное  . Соответствующие проекции равны
. Соответствующие проекции равны
аt = bρ; аn = ω 2 ρ. (12)
Модуль полного ускорения равен а =  .
.
Динамика
Введем некоторые понятия. Материальная точка – это объект, размерами которого можно пренебречь в условиях данной задачи. Система отсчета – это совокупность тела отсчета, жестко связанной с ним системы координат и часов. Допустим, что существует такая система отсчета, в которой изменение скорости материальной точки обусловлено только ее взаимодействием с другими телами. Свободная материальная точка, на которую не действуют другие тела или поля, движется относительно такой системы отсчета прямолинейно и равномерно (= по инерции). Такую систему отсчета называют инерциальной.
Первый закон Ньютона – закон инерции Галилея Ньютона – утверждает, что
существуют такие системы отсчета, называемые инерциальными, в которых материальная точка, на которую не действуют другие тела или поля, движется прямолинейно и равномерно.
Любая система отсчета, движущаяся равномерно и прямолинейно относительно инерциальной, сама также является инерциальной. Действительно, переход к такой системе отсчета приведет к изменению скоростей всех тел на постоянную величину скорости системы отсчета, следовательно, скорость останется постоянной и в другой системе отсчета.
Симметрия пространства и времени. Опыт показывает, что в инерциальных системах отсчета пространство однородно и изотропно, а время однородно. Эти свойства выражают симметрию пространства и времени. Однородность и изотропность пространства означает, что свойства пространства одинаковы в различных его точках (однородность), а в каждой точке одинаковы во всех направлениях (изотропность). Однородность времени означает, что протекание физических явлений в разное время одинаково в одних и тех же условиях.
Принцип относительности Галилея: Во всех инерциальных системах отсчета все законы механики одинаковы. Никакими механическими опытами внутри данной инерциальной системы отсчета невозможно установить, покоится эта система или движется.
 Преобразования Галилея. Пусть инерциальная система отсчета K¢ движется относительно другой инерциальной системы отсчета К со скоростью
Преобразования Галилея. Пусть инерциальная система отсчета K¢ движется относительно другой инерциальной системы отсчета К со скоростью  вправо (рис.5) в направлении совмещенных осей х и х ¢. Начнем отсчет времени с момента, когда начала координат О и О¢ совпадали. Тогда соотношение между радиусами-векторами некоторой точки А в этих системах будет
вправо (рис.5) в направлении совмещенных осей х и х ¢. Начнем отсчет времени с момента, когда начала координат О и О¢ совпадали. Тогда соотношение между радиусами-векторами некоторой точки А в этих системах будет

 , (13)
, (13)
t = t ¢.
Здесь утверждается, что время течет одинаково в обеих системах, а длины отрезков не зависят от состояния движения. Соотношения (13) называются преобразованиями Галилея. В координатном виде преобразования имеют вид
x = x ¢+ Vt, y = y ¢, z = z ¢, t = t ¢. (14)
Продифференцировав (13) по времени, находим преобразование Галилея для скоростей:
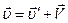 . (15)
. (15)
Дифференцируя это выражение по времени с учетом того, что  = const, получим для ускорений
= const, получим для ускорений
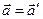 , (16)
, (16)
т.е. ускорения одинаковы во всех инерциальных системах отсчета.
Масса и сила. Влияние на данное тело других тел, если его удалось описать количественно, называют силой. Следовательно, сила – это мера воздействия. Все силы в механике можно разделить на силы, возникающие при непосредственном контакте тел, и действующие через посредство полей (например, силы гравитационные или электромагнитные). Определение силы зависит от определения другого фундаментального понятия – массы.
Масса. Опыт показывает, что всякое тело «оказывает сопротивление» при любых попытках изменить его скорость. Это свойство называют инертностью. Мерой инертности служит масса: чем больше масса, тем более инертным является тело. Введем понятие массы, определив отношение масс двух тел по обратному отношению ускорений, сообщаемых им равными силами:
 . (17)
. (17)
Обратите внимание, как изящно сформулировано последнее предложение: не требуется предварительно вводить способ измерения сил. Достаточно указать источник одинаковых сил, например, разумно допустить, что одинаково растянутая пружина динамометра будет действовать на любую массу с одной и той же силой. Таким образом, сравнение масс двух тел, на которые действует одна и та же сила, сводится к сравнению ускорений этих тел. Выбрав эталон массы, мы имеем возможность сравнить массу любого тела с этим эталоном. Единицей массы в СИ является килограмм (кг). В рамках ньютоновской механики масса обладает следующими свойствами:
1 масса аддитивна, - это значит, что масса тела равна сумме масс его частей.
2 масса тела постоянна, она не зависит от того движется тело, или нет.
Сила. Выше мы допустили, что одинаково растянутая пружина динамометра будет действовать на любую массу с одной и той же силой. С другой стороны, силу мы описали как причину ускорения тел, причем, как показывает опыт, разные массы получают разные ускорения. Одинаковым, как следует из (17) является произведение массы и ускорения:  , которое логично принять за количественное определение силы. Поскольку ускорение – вектор, сила тоже будет вектором.
, которое логично принять за количественное определение силы. Поскольку ускорение – вектор, сила тоже будет вектором.
Окончательно, в классической механике сила, действующая на тело массы m, определяется, как произведение  .
.
Второй закон Ньютона. Если  , как мы только что договорились, то в чем тогда смысл второго закона Ньютона? Это просто определение силы, или что-то большее? Правильный ответ: да, нечто большее. Во-первых, во втором законе Ньютона под
, как мы только что договорились, то в чем тогда смысл второго закона Ньютона? Это просто определение силы, или что-то большее? Правильный ответ: да, нечто большее. Во-первых, во втором законе Ньютона под  понимают силу, далеко не всегда сводящуюся к прямому контакту при взаимодействии. Во-вторых,
понимают силу, далеко не всегда сводящуюся к прямому контакту при взаимодействии. Во-вторых,  может быть суммой многих сил, которые уравновесят друг друга и никакого ускорения не будет, а силы будут присутствовать вполне реально. В-третьих, сила в ряде случаев зависит от окружения данного тела и даже от его скорости (например, сила трения). В-четвертых, второй закон Ньютона можно сформулировать, не вводя понятие силы – в импульсной форме (импульсом материальной точкиназывается произведение ее массы на скорость:
может быть суммой многих сил, которые уравновесят друг друга и никакого ускорения не будет, а силы будут присутствовать вполне реально. В-третьих, сила в ряде случаев зависит от окружения данного тела и даже от его скорости (например, сила трения). В-четвертых, второй закон Ньютона можно сформулировать, не вводя понятие силы – в импульсной форме (импульсом материальной точкиназывается произведение ее массы на скорость: 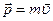 ), и тогда он будет иметь более общий характер, чем дает формула
), и тогда он будет иметь более общий характер, чем дает формула  , хотя в рамках классической механики это различие несущественно. Есть и ещё соображения (вне рамок данного курса), подтверждающие, что в формулировке второго закона Ньютона содержится еще и обобщение введенного понятия силы. Итак:
, хотя в рамках классической механики это различие несущественно. Есть и ещё соображения (вне рамок данного курса), подтверждающие, что в формулировке второго закона Ньютона содержится еще и обобщение введенного понятия силы. Итак:
В инерциальной системе отсчета ускорение тела пропорционально векторной сумме всех действующих на него сил, и обратно пропорционально его массе:
 . (18)
. (18)
Можно дать и другое определение силы: сила есть производная от импульса тела по времени. Тогда второй закон Ньютона в импульсной форме можно сформулировать так
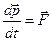 (19)
(19)
Скорость изменения импульса тела равна векторной сумме всех действующих на него сил.
Обратите внимание! Слова «В инерциальной системе отсчета» присутствуют в формулировке не только для украшения! В обеих формулировках подразумевается, что принципиально существует независимый от них способ измерения сил. Следует признать, что изложенные тонкости аксиоматики не препятствуют использованию понятия силы при решении задач, зато очень редко удается на экзамене услышать, что-нибудь вразумительное в ответ на вопрос, что такое сила? Как же должен отвечать на этот вопрос образцовый студент? Я рекомендую «сгрузить» всё подряд, начиная с раздела «Сила» по формулу (19) включительно; а при попытках Вас остановить, следует указать, что без обсуждения второго закона Ньютона это понятие остается недоопределённым и что, если Вам будут мешать, то Вы ещё расскажите и про массу.
Принцип суперпозиции. Опыт показывает, что если есть тела, являющиеся источниками сил, то результирующая сила  , действующая на данную материальную точку, равна
, действующая на данную материальную точку, равна
 (20)
(20)
где 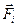 - сила, с которой действовало бы на данную материальную точку i -е тело в отсутствие других тел. Тогда говорят, что эти силы подчиняются принципу суперпозиции.
- сила, с которой действовало бы на данную материальную точку i -е тело в отсутствие других тел. Тогда говорят, что эти силы подчиняются принципу суперпозиции.
Третий закон Ньютона. Из опыта известно, что если на первое тело со стороны второго тела действует сила, то и на это второе тело со стороны первого действует точно такая же сила противоположного направления. Ньютон постулировал это в виде третьего закона:






