Дифференциальное уравнение гармонического осциллятора. Выражения для смещения х и ускорения  отличаются только коэффициентом при cos (…). Поэтому
отличаются только коэффициентом при cos (…). Поэтому  =
=  , или
, или
 (4)
(4)
Это и есть дифференциальное уравнение гармонического осциллятора. Функция (1) - общее решение этого уравнения. Оно содержит две произвольные константы а и a. Их можно найти из начальных условий, например, если даны смещение  и скорость
и скорость  в начальный момент t =0:
в начальный момент t =0:
 ;
;  .
.
Что же такое гармонический осциллятор? Ответ очевиден: кто меняет свою единственную координату по уравнению (1) или (4) – тот и есть гармонический осциллятор. Простейшими примерами гармонических осцилляторов являются грузик на пружинке, математический маятник, физический маятник. И пример для гурманов – вертикальные колебания льдины на воде. Попробуйте понять, что между этими примерами общего.
 Грузик на пружине (пружинный маятник). Пусть грузик массы m подвешен на невесомой пружине жесткостью k. Смещение х будем отсчитывать от положения равновесия (рис.2). В состоянии равновесия пружина растянута под действием силы тяжести m g груза настолько, чтобы сила упругости была в точности равна - m g. Поскольку эти постоянные силы равны и противоположно направлены, они в сумме всегда равны нулю. В процессе колебаний сила упругости будет состоять из двух частей: (1) постоянной составляющей равной mg и (2) переменной составляющей равной kx. Таким образом, в записи второго закона Ньютона для грузика можно не учитывать силу тяжести m g и постоянную составляющую силы упругости (равную - m g). Тогда произведение массы на ускорение равно переменной составляющей силы упругости
Грузик на пружине (пружинный маятник). Пусть грузик массы m подвешен на невесомой пружине жесткостью k. Смещение х будем отсчитывать от положения равновесия (рис.2). В состоянии равновесия пружина растянута под действием силы тяжести m g груза настолько, чтобы сила упругости была в точности равна - m g. Поскольку эти постоянные силы равны и противоположно направлены, они в сумме всегда равны нулю. В процессе колебаний сила упругости будет состоять из двух частей: (1) постоянной составляющей равной mg и (2) переменной составляющей равной kx. Таким образом, в записи второго закона Ньютона для грузика можно не учитывать силу тяжести m g и постоянную составляющую силы упругости (равную - m g). Тогда произведение массы на ускорение равно переменной составляющей силы упругости
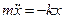 . (5)
. (5)
Редкий ученик понимает, почему справа минус. Возьмите пружинку (хоть из авторучки) и попробуйте её растянуть и сжать. Что Вы заметили? Когда пружину сжимают, она стремится распрямиться (смещение вверх, сила упругости вниз), а когда растягивают, она стремится сжаться (смещение вниз, сила упругости вверх). Таким образом, знаки смещения x и силы kx всегда противоположны, поэтому и минус. Теперь перенесем - kx влево и разделим уравнение (5) на m
 .
.
Правда, похоже на (4)? Чтобы сходство стало полным, обозначим  . Тогда мы получим
. Тогда мы получим  , т.е. дифференциальное уравнение гармонического осциллятора (ГО).
, т.е. дифференциальное уравнение гармонического осциллятора (ГО).
Мораль: коэффициент при x в дифференциальном уравнении гармонического осциллятора равен квадрату циклической частоты этого осциллятора. Если конечно Вы не забыли все уравнение предварительно разделить на коэффициент при  ! А чему же равно x? Раз получено уравнение, идентичное дифференциальному уравнению (4), Þ(1) - его общее решение.
! А чему же равно x? Раз получено уравнение, идентичное дифференциальному уравнению (4), Þ(1) - его общее решение.
Пора спросить: а все ли знают, что точка над x обозначает первую производную по времени от x? Теперь догадайтесь, что означают две точки над x. И начинайте читать все сначала.
Из равенства  следует, что циклическая частота пружинного маятника, зависит от жесткости пружины и массы груза: чем жестче пружина – тем больше частота, чем больше масса груза, тем меньше частота. С периодом все наоборот:
следует, что циклическая частота пружинного маятника, зависит от жесткости пружины и массы груза: чем жестче пружина – тем больше частота, чем больше масса груза, тем меньше частота. С периодом все наоборот:
 ;
; 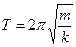 . (6)
. (6)
Пример из министерского тестирования: во сколько раз увеличится период колебаний пружинного маятника, если его массу и жесткость пружины увеличить в 2 раза? Ответ: не изменится. А если массу увеличить в 8 раз, а жесткость пружины увеличить в 2 раза? Ответ: в два раза. И так далее.
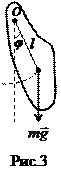 Физический маятник. Это твердое тело, совершающее малые колебания относительно неподвижной оси О, перпендикулярной листу (рис. 3). Запишем основное уравнение динамики вращательного движения в проекции на ось вращения О
Физический маятник. Это твердое тело, совершающее малые колебания относительно неподвижной оси О, перпендикулярной листу (рис. 3). Запишем основное уравнение динамики вращательного движения в проекции на ось вращения О
 (7)
(7)
(слева произведение момента инерции I на угловое ускорение, справа – момент силы тяжести). Чтобы понять, откуда справа минус, вспомним, куда направлены угловое ускорение  и момент силы
и момент силы  . Правильно, оба вектора вдоль оси вращения. А почему всегда в разные стороны? Спрошу на экзамене! Разделим обе части на I; учтем, что для малых углов
. Правильно, оба вектора вдоль оси вращения. А почему всегда в разные стороны? Спрошу на экзамене! Разделим обе части на I; учтем, что для малых углов  ; перенесем все в левую часть, обозначим
; перенесем все в левую часть, обозначим  и получим опять дифференциальное уравнение гармонического осциллятора
и получим опять дифференциальное уравнение гармонического осциллятора
 , (8)
, (8)
только роль смещения вместо x выполняет угол φ. Решение уравнения (8) также совпадает с формулой (1) с точностью до обозначений:  , где для разнообразия амплитуда обозначена φ0. Циклическая частота и период колебаний физического маятника равны
, где для разнообразия амплитуда обозначена φ0. Циклическая частота и период колебаний физического маятника равны
 ;
;  . (9)
. (9)
Такую же частоту и период имеет математический маятник длины lпр =  , которую называют приведенной длиной физического маятника.
, которую называют приведенной длиной физического маятника.
 Математический маятник - это частица массы m, совершающая малые колебания на нити длиной l (в плоскости листа - на рис.4). Основное уравнение динамики вращательного движения будет отличаться только тем, что момент инерции частицы известен (
Математический маятник - это частица массы m, совершающая малые колебания на нити длиной l (в плоскости листа - на рис.4). Основное уравнение динамики вращательного движения будет отличаться только тем, что момент инерции частицы известен ( ), Þ
), Þ  ; Откуда минус? Да оттуда же! Теперь разделим обе части на ml2; учтем, что для малых углов
; Откуда минус? Да оттуда же! Теперь разделим обе части на ml2; учтем, что для малых углов  ; перенесем все в левую часть и получим дифференциальное уравнение гармонического осциллятора (8), где на этот раз
; перенесем все в левую часть и получим дифференциальное уравнение гармонического осциллятора (8), где на этот раз  , Þ циклическая частота и период колебаний математического маятника равны
, Þ циклическая частота и период колебаний математического маятника равны
 ;
;  . (10)
. (10)
Похоже на выражения (6 и 9), но есть и различие: период (и обе частоты) математического маятника не зависят от его массы! А зависят только от 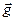 ! Отсюда простейший способ измерения ускорения свободного падения
! Отсюда простейший способ измерения ускорения свободного падения 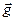 . Берем нить известной длины с грузиком и измеряем период его колебаний. Подставляем в (8) и находим
. Берем нить известной длины с грузиком и измеряем период его колебаний. Подставляем в (8) и находим 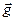 .
.
Пример из министерского тестирования: во сколько раз увеличится период колебаний матема-тического маятника, если его массу увеличить в 2 раза и длину нити увеличить в 2 раза? Ответ: в 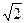 . А если массу увеличить в 8 раз, а длину нити увеличить в 4 раза? Ответ: в 2 раза. И масса в обоих случаях не при чем!
. А если массу увеличить в 8 раз, а длину нити увеличить в 4 раза? Ответ: в 2 раза. И масса в обоих случаях не при чем!
Мораль. Свободные колебания любого осциллятора без трения будут гармоническими, если действующая сила направлена к положению равновесия и пропорциональна смещению от положения равновесия. В примере со льдиной именно так и получается: при вертикальных колебаниях меняется погруженная в воду часть льдины, а Þ и сила Архимеда пропорциональная глубине погружения.
Сложение гармонических колебаний одного направления. Можно условно изображать колебания с помощью вектора амплитуды 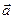 , вращающегося с угловой скоростью w против часовой стрелки, так как проекции этого вектора изменяются по гармоническому закону. Действительно, угол вектора
, вращающегося с угловой скоростью w против часовой стрелки, так как проекции этого вектора изменяются по гармоническому закону. Действительно, угол вектора 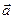 с осью х в момент времени t равен
с осью х в момент времени t равен  , а его проекция на ось х равна а cos
, а его проекция на ось х равна а cos  . Проекция вектора суммы двух векторов равна сумме однонаправленных гармонических колебаний. Такой способ называется векторной диаграммой. Мы рассмотрим два случая: 1- когда частоты складываемых колебаний равны, 2 - когда они мало отличаются.
. Проекция вектора суммы двух векторов равна сумме однонаправленных гармонических колебаний. Такой способ называется векторной диаграммой. Мы рассмотрим два случая: 1- когда частоты складываемых колебаний равны, 2 - когда они мало отличаются.
Термины “ мало- много ” требуют обязательного уточнения: по сравнению с чем? Всем известно, что три волоса на голове – это мало, а в тарелке – много! В нашем случае (колебаний, а не волос) уточнение состоит в том, что разность складываемых частот много меньше каждой из них. Обязательно обращайте внимание на уточнение! Оно неизбежно будет использовано при выкладках. Так, мы недавно использовали (дважды!) термин малые колебания. А уточнение состояло в том, что для них  .
.
 1 Пусть складываются гармонические колебания х 1 и х 2 с одинаковой частотой w. Тогда результирующее смещение равно
1 Пусть складываются гармонические колебания х 1 и х 2 с одинаковой частотой w. Тогда результирующее смещение равно
x = х 1 + х 2 = а 1 cos  + а 2 cos
+ а 2 cos  =
=  .
.
Изобразим колебания векторами 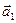 и
и  , которые в начальный момент составляют с осью х углы a 1 и a 2 соответственно (рис.5). Амплитуду а и начальную фазу a результирующего колебания можно найти, как видно из рисунка, из соотношений
, которые в начальный момент составляют с осью х углы a 1 и a 2 соответственно (рис.5). Амплитуду а и начальную фазу a результирующего колебания можно найти, как видно из рисунка, из соотношений
 (11)
(11)

 (12)
(12)
 Из (11) видно, что амплитуда результирующего колебания существенно зависит от разности фаз
Из (11) видно, что амплитуда результирующего колебания существенно зависит от разности фаз 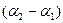 . При сложении синхфазных колебаний (т.е. таких, что
. При сложении синхфазных колебаний (т.е. таких, что 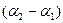 =0) результирующая амплитуда максимальна, а при сложении колебаний в противофазе
=0) результирующая амплитуда максимальна, а при сложении колебаний в противофазе  - минимальна:
- минимальна:  ;
; 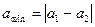 .
.
2 Пусть  и w 2. Это значит, частоты мало отличаются! В этом случае справедлив рис.5. Но теперь векторы
и w 2. Это значит, частоты мало отличаются! В этом случае справедлив рис.5. Но теперь векторы 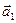 и
и  вращаются с немного отличающимися угловыми скоростями, модуль результирующего вектора
вращаются с немного отличающимися угловыми скоростями, модуль результирующего вектора 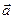 будет медленно (почему?,- спрошу!) изменяться от
будет медленно (почему?,- спрошу!) изменяться от  до
до 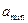 , причем сам вектор
, причем сам вектор 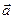 вращается с угловой скоростью, близкой к
вращается с угловой скоростью, близкой к  и w 2. Строго говоря, результирующее колебание не является гармоническим. Его можно рассматривать, как почти гармоническое, но с медленно периодически изменяющейся амплитудой (рис.6). Такие колебания называются биениями. Результирующая амплитуда также может быть выражена формулой (11), но теперь разность фаз
и w 2. Строго говоря, результирующее колебание не является гармоническим. Его можно рассматривать, как почти гармоническое, но с медленно периодически изменяющейся амплитудой (рис.6). Такие колебания называются биениями. Результирующая амплитуда также может быть выражена формулой (11), но теперь разность фаз 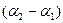 следует заменить выражением d =
следует заменить выражением d =  -
-  =
= 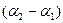 +
+  .
.
Сложение взаимно перпендикулярных колебаний. Рассмотрим несколько случаев.
1. Пусть складываются гармонические колебания х и y с одинаковой частотой w
 и
и  . (13)
. (13)
Поскольку cos любого угла можно записать, как sin дополнительного (до 900) угла, то выражение для y можно представить как  , где a + d =900. Перепишем выражения (13) в виде
, где a + d =900. Перепишем выражения (13) в виде
 ;
; 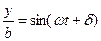 (14)
(14)
Если возвести оба уравнения в квадрат, расписать синус суммы, сложить уравнения и учесть что sin2…+ cos2… =1, то можно исключить время. Так получим уравнение траектории - эллипс (рис.7). Обязательно получите самостоятельно! По этой эллиптической траектории точка будет вращаться с частотой w. Рассмотрим частные случаи.
 а) d =0. Тогда
а) d =0. Тогда  . Эллипс вырождается в наклонный отрезок в первом и третьем квадрантах (рис.8 а). Точка будет гармонически колебаться вдоль этого отрезка с частотой w.
. Эллипс вырождается в наклонный отрезок в первом и третьем квадрантах (рис.8 а). Точка будет гармонически колебаться вдоль этого отрезка с частотой w.
б) d = p. Тогда  . Тоже отрезок, только во втором и четвертом квадрантах (рис.8 б).
. Тоже отрезок, только во втором и четвертом квадрантах (рис.8 б).
 в) d = p/ 2. Тогда получим
в) d = p/ 2. Тогда получим  , Þ частица движется по эллипсу, полуоси которого совпадают с осями координат (рис.8 в). Так как колебание y опережает колебания х на p/ 2 (см. формулы (14)!), то y достигает max раньше, чем х, - поэтому вращение происходит по часовой стрелке.
, Þ частица движется по эллипсу, полуоси которого совпадают с осями координат (рис.8 в). Так как колебание y опережает колебания х на p/ 2 (см. формулы (14)!), то y достигает max раньше, чем х, - поэтому вращение происходит по часовой стрелке.
г) d =3 p/ 2=(- p/ 2); Þ наоборот: колебание х опережает колебания y на p/ 2, Þ тоже вращение по эллипсу, только против часовой стрелки (рис.8 г).
2. Если частоты взаимно перпендикулярных колебаний отличаются в целое число раз, то траектория результирующего колебания представляет собой довольно сложную кривую. Эти кривые называются фигурами Лиссажу.
Затухающие колебания.
 Дифференциальное уравнение затухающих колебаний. В реальной колебательной системе всегда есть силы типа трения, которые приводят к уменьшению амплитуды (и энергии) колебаний. Тогда свободные колебания называются затухающими. Пусть на частицу массы m кроме квазиупругой силы (- kx) действует сила сопротивления, пропорциональная скорости
Дифференциальное уравнение затухающих колебаний. В реальной колебательной системе всегда есть силы типа трения, которые приводят к уменьшению амплитуды (и энергии) колебаний. Тогда свободные колебания называются затухающими. Пусть на частицу массы m кроме квазиупругой силы (- kx) действует сила сопротивления, пропорциональная скорости  . Тогда уравнение второго закона Ньютона будет иметь вид
. Тогда уравнение второго закона Ньютона будет иметь вид  . Перенесем все в левую часть, разделим на m и введем обозначения:
. Перенесем все в левую часть, разделим на m и введем обозначения: 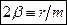 ;
;  ; после чего получим
; после чего получим
 . (15)
. (15)
Циклическую частоту w 0 называют собственной частотой, b - коэффициентом затухания. Уравнение (15) - это дифференциальное уравнение затухающих колебаний. Его решение
 , (16)
, (16)
где а 0 и a - произвольные константы, которые можно найти из начальных условий; Частота затухающих колебаний  , а зависит от b:
, а зависит от b:
 . (17)
. (17)
|
 (пунктир на рис.9). Решение (16) имеет смысл, если
(пунктир на рис.9). Решение (16) имеет смысл, если  . В противном случае в (17) под корнем стоит отрицательная величина и процесс затухает апериодически. Физически это означает, что трение слишком велико, чтобы происходили колебания, хотя бы и с уменьшающейся амплитудой.
. В противном случае в (17) под корнем стоит отрицательная величина и процесс затухает апериодически. Физически это означает, что трение слишком велико, чтобы происходили колебания, хотя бы и с уменьшающейся амплитудой.Время релаксации – это время t, за которое амплитуда колебаний уменьшается в е раз.
Так как  меньше а о в е раз, то
меньше а о в е раз, то  , Þ -1=- bt, Þ
, Þ -1=- bt, Þ  .
.
Логарифмический декремент затухания – это логарифм отношения двух последовательных амплитуд
 .
.
Подставляя в b =1/ t, получим l=Т/t, Þ l - величина, обратная такому числу колебаний, за которое амплитуда уменьшится в е раз!
Вынужденные колебания.
Дифференциальное уравнение вынужденных колебаний. Вынужденные колебания можно получить, если к перечисленным выше силам (квазиупругой = - kx и трения=  ) добавить внешнюю силу, например, периодическую F = F 0cos wt. Тогда по второму закону Ньютона
) добавить внешнюю силу, например, периодическую F = F 0cos wt. Тогда по второму закону Ньютона
 или
или
 , (18)
, (18)
где 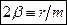 ;
;  ;
;  . Общее решение неоднородного дифференциального уравнения (18) состоит из суммы общего решения однородного уравнения (15) и частного решения неоднородного (18). Общее решение однородного ДУ, как мы видели, затухает со временем. Поэтому остается только частное решение (соответствующее установившимсяколебаниям), которое показывает, что в системе устанавливаются гармонические колебания с частотой w вынуждающей силы, но отстающие от нее по фазе на некоторое φ
. Общее решение неоднородного дифференциального уравнения (18) состоит из суммы общего решения однородного уравнения (15) и частного решения неоднородного (18). Общее решение однородного ДУ, как мы видели, затухает со временем. Поэтому остается только частное решение (соответствующее установившимсяколебаниям), которое показывает, что в системе устанавливаются гармонические колебания с частотой w вынуждающей силы, но отстающие от нее по фазе на некоторое φ
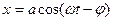 . (19)
. (19)
Если дважды продифференцировать (последний раз предупреждаю, что это значит – взять производную!) уравнение (18), нарисовать векторную диаграмму с учетом сдвига фаз, то можно найти а и φ

 , (20)
, (20)
Резонанс. Первая из формул (20) показывает зависимость амплитуды а от частоты вынуждающей силы (рис.10). При w =0, а =  , а максимум амплитуды соответствует условию
, а максимум амплитуды соответствует условию  . Но еще проще найти минимум только для выражения под корнем, приравняв нулю производную от него. Соответствующая частота w рез называется резонансной
. Но еще проще найти минимум только для выражения под корнем, приравняв нулю производную от него. Соответствующая частота w рез называется резонансной
 w рез=
w рез=  , (21)
, (21)
а само явление достижения максимальной амплитуды называется резонансом. Подставляя в первую из формул (20) резонансную частоту (21), получим максимальную амплитуду
 . (22)
. (22)
Из (22) и рис.10 видно, что чем меньше затухание в системе, тем ярче выражен резонанс. Резонанс используют, если нужно усилить колебания, и, наоборот избегают, если он может привести к нежелательному усилению колебаний.
Упругие волны
Уравнение волны. Упругой волной называется процесс распространения возмущения в упругой среде. При этом сами частицы среды испытывают только колебания около своих положений равновесия. Если колебания частиц происходят вдоль направления распространения, то волна называется продольной, а если перпендикулярно – поперечной.
Рассмотрим для простоты распространение возмущения вдоль длинного натянутого шнура, который совместим с осью х. В качестве возмущения рассмотрим x - смещение элементов шнура из положения равновесия как функцию координаты и времени x=f (x,t). Пусть возмущение распространяется в положительном направлении оси х со скоростью u =  . Тогда в точку с координатой х возмущение придет с опозданием на время
. Тогда в точку с координатой х возмущение придет с опозданием на время  . Итого в момент t в точке х возмущение будет равно x (x,t) =f (t-x/u). Если волна распространяется в отрицательном направлении оси х, то в скобках будет плюс. Выражение в рамочке – это уравнение волны в общем виде. В частности, уравнение плоской гармонической волны имеет вид
. Итого в момент t в точке х возмущение будет равно x (x,t) =f (t-x/u). Если волна распространяется в отрицательном направлении оси х, то в скобках будет плюс. Выражение в рамочке – это уравнение волны в общем виде. В частности, уравнение плоской гармонической волны имеет вид
x (x,t) =аcosw (t-x/u)= аcos (wt-wx/u). (23)
а – амплитуда волны, w - циклическая частота колебаний частиц среды. Функция (23) периодична с периодом 2p и по времени и по координате! Поэтому период равен  . (24) Длиной волны l называется расстояние, проходимое за один период колебаний
. (24) Длиной волны l называется расстояние, проходимое за один период колебаний
l = uT=  , Þ ln=u (25)
, Þ ln=u (25)
Введем волновое число k =  =
=  . Тогда уравнение плоской гармонической волны примет симметричный вид x (x,t) =аcos (wt-kx). (26)
. Тогда уравнение плоской гармонической волны примет симметричный вид x (x,t) =аcos (wt-kx). (26)
Легко показать, что u - это фазовая скорость (т.е. скорость распространения вдоль ох некоторой зафиксированной фазы). Действительно, зафиксируем фазу в (23): пусть t-x/u =const. Þ  , что и требовалось доказать.
, что и требовалось доказать.
Если волна распространяется в поглощающей среде, то ее амплитуда а будет уменьшаться экспоненциально (из опыта), тогда уравнение волны будет иметь вид
 (27)
(27)
В плоской волне волновые поверхности (т.е. геометрическое место точек, колеблющихся в одинаковой фазе) имеют вид плоскостей, (в нашем случае плоскости ^ оси х). Если волновые поверхности - сферы, то волна называется сферической. Фронтом волны называется волновая поверхность, отделяющая область волнового процесса от невозмущенной части среды.
Волновое уравнение. Пусть дано уравнение волны x (x,t) =f (t-x/u), обозначим фазу φ =(t-x/u) и вычислим частные производные по времени и по координате:
 ;
;  , Þ
, Þ
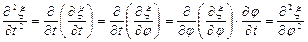 ; Þ
; Þ  (28)
(28)






