Сызықтық жүйенің сипаттамалық теңдеуі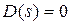 
ашық түрде мына тұлғада берілсін
. (5.43)
Гурвиц критерийі бойынша сызықтық жүйенің орнықтылығы үшін қажетті және жеткілікті, төмендегі матрицаның n бас анықтауыштарының оң болғаны
.
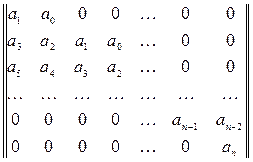Мұндағы матрица берілген жүйе (5.43) сипаттамалық теңдеуінің коэффициенттерінен құрастырылады.
Аталған бас анықтауыштардың түрі төмендегідей
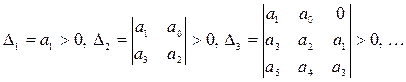. (5.44)
Олар Гурвиц анықтауыштары деп аталады. Гурвицтің соңғы анықтауышы 
мәніне тең. Сондықтан, оның оң болуы келесі шарттардың орындалуын талап етеді
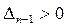және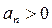 
.
Орнықтылық шекарасын табайық.
1) Апериодикалық орнықтылық шекарасы (нольдік түбір), бұл теңдеу (5.43) сәйкес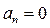 
болғанда туындайды және басқа Гурвиц анықтауыш-тарының оң болғандығымен сипатталады (соңғысынан басқасының).
2) Тербелмелі орнықтылық шекарасы сипаттамалық теңдеудің қос таза жорамал түбірлерімен сипатталады және егер
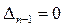(5.45)
болғанда пайда болады. Сонымен қатар, қалған Гурвиц анықтауыштары оң болуы қажет.
3) Шексіз түбірге сәйкес келетін орнықтылық шекарасы теңдеу (5.43) бойынша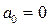 
болғанда алынады. Шындығында да, егер (5.43) теңдеуінің барлық мүшелерін sn бөлсек, аламыз
.
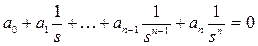Осыдан көрініп тұр, 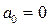болғанда, аламыз 
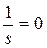, егер s = ∞ болса.
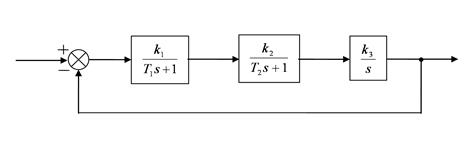
Мысал қарастырайық. Тұйықталмаған жүйе тізбегінің берілу функция-сы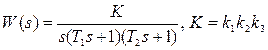 
мына түрде кескінделсін (сурет 5.12).
Сурет 5.12
Тұйықталған жүйенің сипаттамалық теңдеуі келесі түрде болады
.
Оның коэффициенттері оң. Гурвиц критерийі бойынша орнықтылық шарты мына түрде алынады
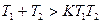немесе 
. (5.46)
Орнықтылық шекаралары:
1) 
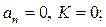
2) 
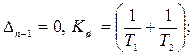
3) 
Бұл үш орнықтылық шекараларын K, T 1, T 2 параметрлерінің кеңістігінде график түрінде кескіндеуге және жүйенің орнықтылық аймағын табуға болады. Ең алдымен бір параметр K (тұйықталмаған жүйе тізбегінің жалпы күшейту коэффициенті) бойынша жүйенің орнықтылық аймағын табамыз. Мұнда параметрлер кеңістігі жалғыз түзу сызық, ал орнықтылық шекарасы – ондағы нүктелер: K = 0 және K = Kш (сурет 5.13). Орнықтылық аймағы (5.46) сәйкес осы нүктелер арасында жатады.
Сурет 5.13
Жүйе орнықтылығының сол үш шекарасын екі параметр жазықтығында да кескіндеуге болады, мысалы: K, T 1. Бірінші шекара (K = 0) T 1 осінде жатады (сурет 5.14). Екінші шекара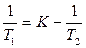 
гипербола түрінде кескінделеді T 1 = 0 және 
асимптоталарымен сипатталады. Үшінші шекара (T 1 = 0) K осімен беттеседі.
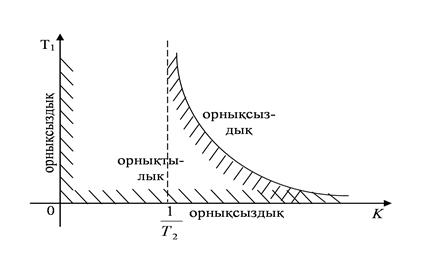
Сурет 5.14
(5.46) теңсіздігімен анықталатын орнықтылық аймағы сурет 5.14 көрсетілген. Шекараны штрихтау орнықтылық аймағына қарай жасалады.
Көрініп тұрғандай, T 1, T 2 уақыт тұрақтылары ұлғайған кезде орнықтылық аймағы тарылады. Сондай-ақ, орнықтылыққа күшейту коэффициенті K ұлғайуы да кері әсерін тигізеді. Кез келген берілген T 1 және T 2 үшін өзінің Kш коэффициенті болады (сурет 5.13), одан кейін жүйе орнықсыз болады.
Бұл өте маңызды жағдай, өйткені басқару дәлдігін жоғарылату үшін K ұлғайту керек. Осыдан қайшылық туады, дәлдік талабы (K өсірілуі) мен орнықтылық (K -ны шектеу) арасында. Осылайша, орнықтылық аймағын K, T 1, T 2 үш параметр арқылы көрсетуге де болады.
