5.5.1 Михайлов критерийі
Михайловтың орнықтылық критерийі жиіліктік критерийлердің қатарына жатады және годографтың түрі бойынша тұйықталған жүйенің орнықтылығын бағалауға мүмкіндік береді. Годографты сипаттамалық теңдеуден алуға болады
. (5.28)
деп ұйғарайық, онда аламыз
. (5.29)
Жиілік (
; 
) аралығында өзгергенде (5.29) теңдеуі комплексті жазықтықта годографты салуға мүмкідік береді және оның түрі бойынша жүйенің орнықтылығы туралы қорытындылауға болады.
Сипаттамалық теңдеу (5.28) n түбірі 
болады, олардың ішінде нақты, комплексті және жорамал қос-қостан түйіндес, сондай-ақ нольдік түбірлер болуы мүмкін.
(5.28) теңдеуін әрқашанда мына түрге келтіруге болады
. (5.30)
Егер , онда (5.30) өрнегі мына түрді қабылдайды
, (5.31)
яғни
, (5.32)
мұнда 
- D (jω) векторының модулі;
- D (jω) векторының аргументі.
Сипаттамалық теңдеудің түбірлері s 1, s 2, …, sn болып табылады, сондай-ақ (5.31) өрнегінің оң жағындағы (jω - si) көбейткіштері комплексті жазықтықта сәйкес векторлармен кескінделеді (сурет 5.5).
Мысалы, s 1 мен s 2 комплексті түйіндес қос түбірлер болып табылады және сол жақ жарты жазықтықта (А және В нүктелері) жатқан ОА және ОВ векторларымен сипатталады. тәуелсіз айнымалысы жорамал осьтегі Е нүктесі арқылы белгіленіп және оны А мен В нүктелері арқылы түзу сызықпен қосып, АЕ және ВЕ векторларын аламыз, ал олар (jω – s 1) және (jω – s 2) көбейткіштеріне сәйкес болады. Ұқсастық бойынша қалған түбірлер үшін де кескіндеулерді орындауға болады және осылайша әр (jω - si) көбейткішін сәйкес вектормен кескіндейміз.
Сурет 5.5
Ұйғарайық, n дәрежелі сипаттамалық теңдеудің барлық түбірлерінің ішінде m түбірі оң жарты жазықтықта орналасып, ал қалған n – m түбірі жорамал осьтің сол жағында орналасқан және теріс нақты бөлікті болады деп. D (jω) векторы аргументінің өзгеруін, яғни жиілік (; ) аралығында өзгергендегі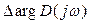 
табамыз. 
болады, онда жиілк көрсетілген диапазонда өзгергенде барлық (jω – si) векторлары аргументтері-нің өзгеруінің қосындысы D (jω) векторы аргументінің өзгеруін анықтайды.
Жиілік ω минус шексіздіктен 
плюс шексіздікке 
дейін өзгерген кезде Е нүктесі комплексті жазықтықтың жорамал осінде орналасады да (сурет 5.5), минус шексіздіктегі орнынан плюс шексіздіктегі орынға жылжиды. Бұл сипаттамалық теңдеудің si түбірі анықталатын нүктелердің айналасында (jω – si) векторларының айналуын ту-дырады. Сол жақ жарты жазықтықта орналасқан түбірлер үшін (jω – si) век-торларының әрқайсысы сағат тіліне қарама-қарсы айналатын болады және жиілік минус шексіздіктен плюс шексіздікке дейін өзгерген кезде олардың әрқайсысы 180о айналады.
Мысалы, (jω – s 1) және (jω – s 2) векторлары А және В нүктелерінің маңайын айнала отырып, сағат тіліне қарсы әрқайсысы +180о бұрылады (сурет 5.5). Оң жақ жарты жазықтықта орналасқан түбірлер үшін, сәйкесінше (jω – si) векторлары сағат тілі бойынша –180о айналатын болады, мысалы, (jω – s 4) және (jω – s 5) векторлары жиілігі сол көрсетілген шекте өзгерген кезде, –180о бұрылады. Сағат тіліне қарсы айналуды оң, ал сағат тілі бойынша айналуды теріс деп қабылдай отырып, қорытынды жасауға болады: ω жиілігі минус шексіздіктен плюс шексіздікке дейін өзгерген кезде, сол жақ жарты жазықтықта орналасқан (jω – si) векторларының әрқайсысы өз аргументін +180о өзгертеді, ал оң жақ жарты жазықтықта болатын (jω – si) векторларының әрқайсысы –180о өзгертеді. Сол жақ жарты жазықтықтағы түбірлердің саны n – m болғандықтан, (jω – si) түрлі сол жақ векторлардың жалпы аргументтерінің өзгерісі (n – m) π тең болады. Оң жақ жарты жазық-тықта m түбір орналасқан, ал барлық оң векторлардың аргументтерінің жалпы өзгерісі – mπ тең шаманы тудырады. Жиілік ω минус шексіздіктен плюс шексіздікке дейін өзгерген жағдайда D (jω) векторы аргументінің қорытынды нәтижелік өзгеруі
. (5.33)
Формула (5.33) орнықсыз жүйенің D (jω) векторы аргументінің өзгерісін анықтайды, себебі m ≠ 0. m = 0 деп ұйғарсақ, табамыз
. (5.34)
Формула (5.34) орнықты жүйенің D (jω) векторы аргументінің өзгеруін анықтайды және барлық түбірлер сол жақ жарты жазықтықтан табылған жағдайға сәйкес болады.
Теріс жиілік диапазонын 
алып тастауға болады, себебі D (jω) годографы оң жиілік үшін және D (- jω) годографы теріс жиілік үшін нақты оське қатысты симметриялы орналасқан. Бұл мынадан шығады
, (5.35)
мұндағы ω айнымалысына қатысты 
- жұп функция, ал 
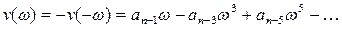- тақ функция.
Теріс жиілік диапазонын алып тастау D (jω) векторы аргументінің өзгеруін екі есеге кішірейтеді. (jω - si) векторлары жиілік нольден (0) плюс шексіздікке дейін өзгергенде аргументтің өзгерісі екі есе кіші болады, қарастырылған жағдай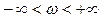 
салыстырғанда.
Сонымен, (5.34) формуласын мына түрде көрсетуге болады
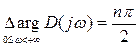. (5.36)
Формула (5.36) тұйықталған жүйе орнықтылығының қажетті және жеткілікті шартын анықтайды және сонымен қатар, Михайлов критерийінің математикалық жазылуы болады.
Михайловтың орнықтылық критерийі: тұйықталған күйдегі жүйенің орнықтылығы үшін қажетті және жеткілікті, жиілік нольден (0) плюс шексіздікке дейін өзгерген кезде D (jω) векторы өз ұшымен Михайлов қисығын сызып, өзінің қозғалысын нақты оң осьтен бастап және сағат тіліне қарсы айналып, еш жерде нольге айналмай ретімен n квадранттан өткені.
Орнықты жүйе үшін Михайлов қисықтары сурет 5.6а) көрсетілген, онда сипаттамалық теңдеулер реті n = 1,3,5.
n = 3 болғанда D (jω) векторы жиілік өскен кезде координаталар басы айналасында сағат тіліне қарсы бұрылып, ретімен үш квадрантты: I, II және III өтеді. III квадрантта D (jω) векторының модулі шексіз үлкен болып өседі. n = 5 болғанда D (jω) векторы I, II, III IV квадранттарынан және қайтадан I квадранттан өтеді. Бұл жағдайларда D (jω) векторы еш жерде нольге айналмайды.
а) б) в)
Сурет 5.6
Егер критерийде жазылған шарт бұзылса, онда жүйе орнықсыз болады. Орнықсыздық белгілері ретінде мына жағдайлар қарастырылуы мүмкін: Михайлов қисығы оң нақты осьтен басталмауы мүмкін (n = 1 болғанда годограф 1, сурет 5.6б); Михайлов қисығы координаталар басы арқылы өтеді (n = 3 болғанда годограф 1, сурет 5.6в); D (jω) сипаттамалық векторының квадранттарды өту реті бұзылады (годограф 2, сурет 5.6б).
