Орнықтылықтың алгебралық критерийлері деп жүйенің сипаттамалық теңдеуінің коэффициенттерінен құрастырылған сондай шарттарды айтамыз, олар орындалған кезде жүйе орнықты, ал орындалмаған кезде орнықсыз болады.
Алгебралық критерийлердің көмегімен орнықтылықты зерттеуді жүргізген кезде, ең алдымен орнықтылықтың қажетті шартының орындалуын тексеру керек, себебі оны тексеру ешқандай есептеулерді қажет етпейді және ол орындалмаған жағдайда әрі қарай зерттеудің керегі болмайды, өйткені жүйенің орнықсыздығы белгілі болады.
Алгебралық критерийлердің көмегімен орнықтылықты зерттеу үшін, сипаттамалық полиномды білу керек. Егер беру функциясы берілген болса, онда сипаттамалық полином ретінде оның бөліміндегі көпмүшелікті алуға болады. Тұйықталған жүйенің орнықтылығын зерттеу кезінде тұйықталмаған жүйенің 
беру функциясы белгілі болса, онда тұйықталған жүйенің сипаттамалық полиномы тұйықталмаған жүйенің беру функциясының алымындағы және бөлінімдегі полиномдардың қосындысына, яғни 
тең.
Гурвиц критерийі
Сызықтық жүйенің сипаттамалық теңдеуі берілсін
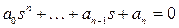. (5.11)
Орнықтылықты анықтау үшін сипаттамалық теңдеудің коэффициенттерінен келесі түрде матрица құрастыру қажет
. (5.12)
(5.12) матрицасын құрастырған кезде ең алдымен диагональ бойынша солдан оңға қарай a 1 бастап сипаттамалық теңдеудің коэффициенттерін әрі қарай индекстерінің өсу ретімен aп дейін (aп қосып есептегенде) жазылады. Жатық жолдар диагональдан оңға қарай индекстерінің кему реті бойынша коэффициенттермен толтырылады. Осы кезде теріс индексті коэффициенттер нольдермен алмастырылады. Жатық жолдарда диагональдан солға қарай индекстерінің өсу ретімен коэффициенттер қойылады. Сипаттамалық теңдеудің реті n асатын индексті коэффициенттер нольмен алмастырылады.
Критерий. Орнықтылық шарты орындалу үшін және осыдан туындайтын сипаттамалық теңдеудің түбірлері теріс нақты бөлікті болуы үшін қажетті және жеткілікті, (5.12) матрицасының барлық n диагональ-дық минорларының оң болғаны, яғни келесі теңсіздіктердің орындалғаны
(5.13)
(5.12) матрицасының диагональдық минорлары Гурвиц анықтауыштары деп аталады. Гурвиц критерийі бойынша бірінші және екінші ретті жүйелердің орнықтылығы үшін жүйенің сипаттамалық теңдеуінің барлық коэффиценттерінің оң болғаны қажетті және жеткілікті. Үшінші және одан да жоғары ретті жүйелер үшін бұл шарттың орындалуы қажетті, бірақ жеткілікті болмайды.
Мысал 1. Төртінші ретті сипаттамалық теңдеу берілсін
. (5.14)
Гурвиц критерийі бойынша
(5.15)
теңсіздіктерінің орындалғаны орнықтылықтың қажетті және жеткілікті шарттары болады
(5.15) теңсіздіктерінің орындалуы үшін ең алдымен барлық а 0, а 1, а 2, а 3, а 4 коэффициенттерінің оң болғаны қажет екенін байқау қиын емес. Коэффициенттер оң болған кезде, тағы да қосымша Δ2 және Δ3 Гурвиц анықтауыштарының нольден үлкен болу шарттарының орындалуы қажетті. Бұл қосымша шарттар Гурвиц анықтауыштары (5.15) екінші және үшінші тңсіздіктеріне қатысы бар жүйе коэффициенттерінің белгілі бір қатынаста болғанын және кез келген еркін оң мәндер емес, теңсіздіктер 
болғанын сәйкес талап етеді.
Льенар-Шипар критерийі
Егер орнықтылықтың қажетті шарттары орындалатын болса, онда жүйенің орнықтылығын анықтау үшін Гурвицтің барлық анықтауыштарын есептеудің қажеті болмайды.
Критерий. Орнықтылықтың қажетті шарттары орындалған кезде 
, жүйенің орнықтылығы үшін қажетті және жеткілікті, оның барлық жұп индексті Гурвиц анықтауыштарының немесе оның барлық тақ индексті Гурвиц анықтауыштарының оң болғаны, яғни
, (5.16а)
немесе
(5.16б)
Есептеулерді азайту үшін п тақ болғанда (5.16а) шарттары, ал п жұп болған кезде (5.16б) шарттары пайдаланылады.
Мұнда Льенар-Шипар критерийінің біраз қарапайымдалған тұжырымдамасы келтірілген. (5.16а) немесе (5.16б) шарттарының біреуі орындалған кезде орнықтылық шартындағы қажет теңсіздіктердің барлығы бірдей тәуелсіз болуы мүмкін болмайды. Сондықтан, теңсіздіктердің кейбір бөлігін қарастырмауға да болады. Бірақ, орнықтылықтың қажетті шарттарын тексеру есептеулермен байланыссыз болғандықтан, бұған біз тоқталмайтын боламыз.
жағдайлары үшін орнықтылықтың қажетті және жеткілікті шарттарын жазып, Льенар және Шипар критерийлерінен аламыз
Осыдан, 
және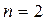 
болғанда орнықтылықтың қажетті шарттарының өзі жеткілікті болады. Бірақ, 
болған кезден бастап орнықтылық үшін орнықтылықтың қажетті шарттарының орындалуынан басқа, ортаңғы коэффициенттерінің көбейтіндісі мен шеткі коэффициент-терінің көбейтіндісінің өзара айырымының оң болғаны қажет екенін аламыз.
Мысал 2. Тұйықталмаған жүйенің беру функциясы берілсін
Тұйықталмаған және тұйықталған жүйенің орнықтылығын зерттейік.
Шешімі. Тұйықталмаған жүйенің сипаттамалық полиномы 
болады. Барлық коэффициенттері нольден үлкен және анықтауышы 
. Сондықтан тұйықталмаған жүйе орнықты.
Тұйықталған жүйенің сипаттамалық полиномы
.
Бұл полиномның барлық коэффициенттері k -ның екі мәнінде де оң болады, ал Δ2 анықтауышы 
болғанда 
.
Осыған байланысты, тұйықталған жүйе болған кезде орнықты, ал 
болған кезде орнықсыз болады.
Мысал 3. Тұйықталмаған жүйенің беру функциясы берілсін
Тұйықталмаған және тұйықталған жүйенің орнықтығын зерттейік.
Шешімі. Тұйықталмаған жүйенің сипаттамалық полиномы 
болады. Оның коэффициенттері 
және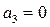 
. Орнықтылықтың қажетті шарты орындалмайды, сондықтан тұйықталмаған жүйе орнықсыз.
Тұйықталған жүйенің сипаттамалық полиномы
болады. Барлық коэффиценттері k -ның екі мәнінде де оң болады, яғни Δ2 анықтауышы k = 0,5 болса
,
ал k = 2 болғанда
.
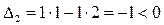Осыдан, тұйықталған жүйе k = 0,5 болған кезде орнықты болады, ал k = 2 болғанда орнықсыз болады.
Қарастырылған мысалдардан, тұйықталмаған жүйе орнықсыз болуы мүмкін, ал тұйықталған жүйе орнықсыз немесе керісінше орнықты болуы мүмкін екені шығады. Одан басқа тұйықталған жүйенің орнықтылығы тұйықталмаған жүйенің беру коэффициентіне тәуелді болады.
Мысал 4. Жүйенің сипаттамалық полиномы берілсін
,
оның орнықтылығын зерттеу керек.
Шешімі. Бұл жағдайда n = 4 – жұп сан. Сондықтан, (5.16б) шартын пайдаланған қолайлы. Орнықтылықтың қажетті шарты орындалады, яғни барлық коэффициенттері 
оң. (5.16б) шартына сәйкес Δ3 анықтауышын есептеу жеткілікті, яғни
Ендеше жүйе орнықты.
