Определение 6.8. Суммой (разностью, произведением) функций f и g называется функция f+g (f–g, fg), область определения которой 
(
, 
), а значения вычисляются по формуле (f+g)(х)=f(x)+g(x), (f–g)(x) =f(x)–g(x), (fg)(x)=f(x) g(x).
Пример 6.9.
Определение 6.9. Частным функций f и g называется функция 
, область определения которой 
, причём исключаем те х, для которых
g (х)=0, а значения вычисляются по формуле 
.
Пример 6.10.
Определение 6.10. Пусть y является функцией переменной u,а переменная u, в свою очередь, является функцией от переменной х, то есть 
и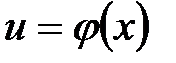 
. Тогда функция 
называется функцией от функции (или сложной функцией), если область определения функции f содержит множество значений функции j. Переменная и в этом случае называется промежуточной переменной.
Пример 6.11.
П.5. Обратная функция
Определение 6.11. Пусть функция 
определена и возрастает (убывает) на промежутке Х, а область значений функции есть промежуток Y. Каждому значению у 0 из промежутка Y будет соответствовать одно значение х 0 Î Х такое, что 
(рис. 13). Следовательно, на промежутке Y определена функция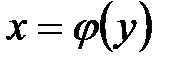 
. Функция 
называется обратной для функции и, наоборот, функция является обратной для функции .
Рис. 13
Переход от функции к обратной функции сводится только к изменению роли множеств Х и Y. Поэтому графики функций и (как множества точек плоскости хОу) совпадают. Однако обычно и для обратной функции аргумент обозначают через х, а значения функции –– через у, то есть вместо пишут 
. Графики функции и обратной функции 
в этом случае будут симметричны относительно прямой у = х (рис. 14).
Рис. 14
Пример 6.12.
П.6. Основные числовые функции и их графики
Основными элементарными функциями называются следующие: степенная функция 
, где a любое действительное число; показательная функция 
, где а >0, a ≠1; логарифмическая функция 
, где а >0, a ≠1; тригонометрические функции y = sin x, y = cos x,
y = tg x, y = ctg x; обратные тригонометрические функции y = arcsin x, y = arccos x, y = arctg x, y = arcctg x.
Линейная функция.
Квадратичная функция.
Степенная функция. Область определения степенной функции 
зависит от показателя a. Эта функция при любом a определена в интервале 0 < х < +¥, то есть для всех положительных значений х. При a натуральном областью определения является вся числовая ось. Множеством значений функции будет интервал 0 < у < +¥ при a четном и промежуток –¥ < у < +¥ при a нечетном (рис. 15).
Рис. 15
Показательная функция. Областью определения показательной функции 
является вся числовая ось, то есть промежуток (–¥; + ¥), а множеством значений функции - промежуток (0; + ¥) (рис. 16).
Рис. 16
Логарифмическая функция. Областью определения логарифмической функции 
является промежуток 
, а множеством значений функции - промежуток 
(рис. 17).
Рис. 17
Тригонометрические функции. Областью определения функций y = sin x и y = cos x является промежуток , а множеством значений функций –– отрезок [–1; 1] (рис. 18 и 19).
Рис. 18 Рис. 19
Функция 
определена на всей числовой оси, кроме точек 
, т.е. область определения этой функции есть совокупность интервалов
.
Функция 
определена на всей числовой оси, кроме точек 
, т.е. область определения этой функции состоит из интервалов
.
Множеством значений функций 
и является промежуток (рис. 20 и 21).
Рис. 20 Рис. 21
Обратные тригонометрические функции. Областью определения функций y = arcsin x и
y = arccos x является отрезок [– 1; 1]. Множеством значений функции y = arcsin x является отрезок 
, а функции y = arccos x –– отрезок 
(рис. 22 и 23).
Рис. 22 Рис. 23
Областью определения функций y = arctg x и y = arcсtg x является промежуток . Множеством значений функции y = arctg x будет интервал 
, а функции y = arcсtg x –– интервал 
(рис. 24 и 25).
Рис. 24 Рис. 25
