В этом параграфе будем рассматривать только числовые множества и кратко будем называть их «множества».
Определение 5.1. Множество Х называется ограниченным сверху (снизу), если существует такое число M (m), что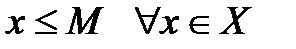 
(
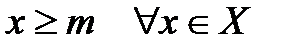). Число M (m), называется верхней (нижней) границей множества Х.
Пример 5.1. Найти верхнюю и нижнюю границы множеств:
Определение 5.2. Множество Х называется ограниченным, если оно ограничено и сверху и снизу, т.е. существуют такие числа M и m, что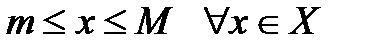 
. В противном случае оно называется неограниченным.
Это определение равносильно следующему
Определение 5.3. Множество Х называется ограниченным, если существует такое число M >0, что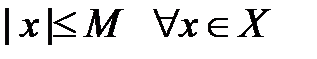 
. Множество Х называется неограниченным, если для любого числа M >0 существует такое число 
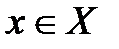, что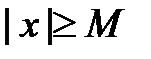 
.
Определение 5.4. Наименьшая (наибольшая) из верхних (нижних) границ ограниченного сверху (снизу) множества Х называется верхней (нижней) гранью множества Х и обозначается sup X (inf X), читается supremum (infimum).
Свойства верхней и нижней граней множества
1о. Если a* = sup X, то
1) 
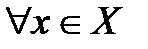выполняется неравенство 
.
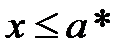2) 
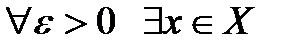такое, что выполняется неравенство 
.
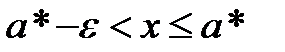2о. Если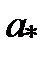 
= inf X то
1) 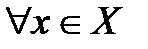выполняется неравенство 
.
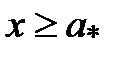2) 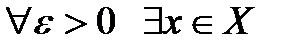такое, что выполняется неравенство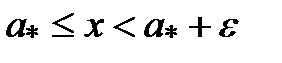 
Теорема 5.1. Всякое ограниченное сверху (снизу) множество имеет верхнюю (нижнюю) грань и при том только одну.
Дано.
Доказать.
Доказательство.
Замечание 5.1. Если множество Х неограниченно сверху (снизу), то будем считать sup X =+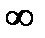 
(inf X =– 
).
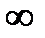В заключение приведем
Аксиому Архимеда. Каким бы ни было действительное число k, всегда есть натуральное число n, которое больше k.
Из этой аксиомы следует, что множество натуральных чисел неограниченно.
Пример 5.2. Найти верхнюю и нижнюю грани множеств:
ДЕЙСТВИТЕЛЬНЫЕ ФУНКЦИИ ОДНОЙ ДЕЙСТВИТЕЛЬНОЙ
ПЕРЕМЕННОЙ
П.1. Понятие функции
На практике мы часто встречаемся с зависимостями между разными величинами.
Изучение зависимости между объектами состоит в том, что между ними устанавливается соответствие.
Определение 6.1. Соответствие между множествами X и Y, при котором каждому элементу х множества Х соответствует один и только один элемент у множества Y, называется функцией, заданной на множестве X со значением в множестве Y.
Функция обозначается при помощи латинской (а иногда греческой) буквы, например, буквы f.
Элемент х Î Х называется аргументом или независимой переменной функции f. Множество всех таких элементов х Î Х называют областью определения функции f и обозначают D (f) (D (f)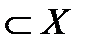 
). А элемент y Î Y, соответствующий элементу х, называется значением функции f и обозначается f (х). Множество, состоящее из всех значений функции f, называют областью (множеством) значений функции f и обозначают Е (f) ( Е (f) 
).
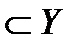Заметим, что если у Î Е (f), то существует по крайней мере один такой х Î D (f), что f (х) = у.
Функцию f, заданную на множестве X со значениями в множестве Y, обозначают также следующим образом:
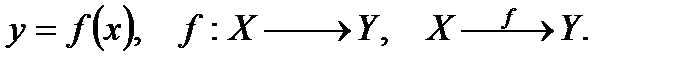
Определение 6.2. Две функции f и g называют равными (пишут f = g), если D (f) = D (g) и f (х) = g (х) для каждого х Î D (f).
Функции называются также отображениями. Если функция f задана на паре множеств Х и Y, т.е. f Ì Х ´ Y, то говорят, что f есть отображение из Х в Y.
Если X = D (f) и Е (f) Ì Y, то говорят, что f есть отображение множества Х в Y.
Если X = D (f) и Y = Е (f), то говорят, что f есть отображение множества Х на Y.
Определение 6.3. Функция f, область определения и область значений которойсостоят из некоторого множества действительных чисел, называется действительной функцией одной действительной переменной.
Ниже для краткости будем говорить «функция», подразумевая действительную функцию одной действительной переменной.
Функция считается заданной, если выполнены следующие два условия:
1) заданы два числовых множества Х и Y;
2) задан способ (правило), при помощи которого каждому числу х Î Х ставится в соответствие единственное число y Î Y.
