1. Аналитический, т. е. с помощью формулы. Если функция задана формулой и не дано дополнительных ограничений, то областью определения функции считают множество всех значений переменной, при которых эта формула имеет смысл. Иногда функция задается в области определения не одной формулой, а несколькими разными формулами. Пример 6.1. Функция
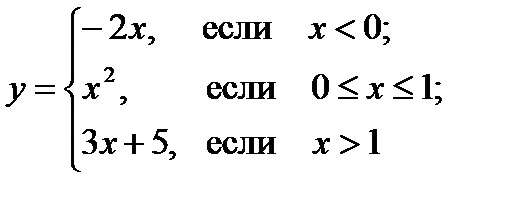
задана аналитическим способом на множестве действительных чисел при помощи трех разных формул.
Пример 6.2. Функция Дирихле
Пример 6.3. y=sgn x
2. Табличный способ.
3. Словесный (описывают словами закон, по которому находятся значения функции).
Пример 6.4. Функция f каждому квадрату со стороной а ставит в соответствие его площадь. S (a)= a 2, a>0.
Пример 6.5. Каждому действительному числу х поставим в соответствие наибольшее целое число, которое не превосходит y. Эта функция – Антье, обозначается E (x)=[ x ], её график.
4. Графами.
5. Графический ( только для числовых функций числового аргумента).
Определение 6.4. Графиком функции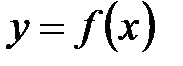 
, заданной на множестве Х, называется множество всех точек плоскости с координатами 
, где х Î D (f).
Заметим, для того чтобы некоторое множество точек плоскости являлось графиком какой–либо функции, необходимо, чтобы это множество имело не более одной общей точки с любой прямой, параллельной оси Оу.
Рис. 10 Рис. 11
П.3. Основные свойства
1.Монотонныефункции
Определение 6.5. Пусть функция 
задана на некотором множестве Х. Данная функция называется возрастающей (убывающей) на множестве Е Ì Х, если для любых х 1 и х 2 из множества Е, таких что х 1 < х 2, выполняется неравенство
.
Иначе: функция f называется возрастающей (убывающей) на множестве Е, если большему значению аргумента из этого множества соответствует большее (меньшее) значение функции (рис. 12).
Рис.12
Если же для любых значений х 1, х 2, взятых из некоторого множества Е Ì Х и удовлетворяющих условию х 1 < х 2, вытекает некоторое неравенство f (х 1) £ f (х 2) (или f (х 1) ³ f (х 2)), то функция называется неубывающей (невозрастающей) на множестве Е.
Пример 6.6. Доказать, что сумма двух возрастающих (убывающих) на множестве Е функции есть функция возрастающая (убывающая) на этом множестве.
2. Функции чётные и нечётные
Определение 6.6. Функция называется четной (нечетной), если при изменении знака у любого значения аргумента, взятого из области определения функции, значения функции не изменяются (изменяют только знак), т.е. 
.
График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.
Пример 6.7. Доказать, что произведение чётной функции на нечётную есть функция нечётная.
3. Периодические функции
Определение 6.7. Функция называется периодической, если существует такое число l ¹ 0 (называемое периодом), что в каждой точке области определения функции выполняется условие 
.
Пример 6.8. Доказать, что если число l - период функции, то число kl (k =-1, ±2, …) также является периодом.
4. Ограниченные и неограниченные функции
