Из СШ известны следующие обозначения:
N – множество натуральных чисел,
Z – множество целых чисел,
Z0 – множество целых неотрицательных чисел,
Q – множество рациональных чисел,
I – множество иррациональных чисел,
R – множество действительных чисел.
В курсе СШ под действительным числом понимают бесконечную десятичную дробь без 9 в периоде. Если бесконечная десятичная дробь – периодическая, то это рациональное число, а если бесконечная десятичная дробь – непериодическая, то это иррациональное число.
Из курса математики СШ известно, что множество, состоящее и рациональных и иррациональных чисел, называется множеством действительных чисел (R). На множестве R вводятся операции «сложения», «умножения», отношение порядка (сравнение). Формулируются 3 группы аксиом:
I. Аксиомы сложения и умножения
1. a + b = b + a
2. a + (b + c)= (a + b) + c
3. a ∙ b = b ∙ a
4. a ∙ (b ∙ c)= (a ∙ b) ∙ c
5. (a + b) ∙ c= a ∙ c + b ∙ c
6. Существует число 0 такое, что а + 0 = а для любого действительного числа а
7. Для любого действительного числа а существует число – а такое, что а + (– а) = 0
8. Существует число 1≠0 такое, что а ∙ 1 = а для любого действительного числа а
9. Для любого действительного числа а ≠0существует число а –1 такое, что а ∙ а –1 = 1
II. Аксиомы порядка
Для любых 
1. Для любых  либо
либо 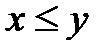 , либо
, либо  .
.
2. Если  , то x=y.
, то x=y.
3. Если 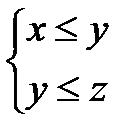 , то
, то  .
.
4. Если х ≤ у, то для любого z выполняется х + z ≤ у + z
5. Если х ≤ у, то для любого z > 0 выполняется х ∙ z ≤ у ∙ z,
а для любого z < 0 выполняется х ∙ z ≥ у ∙ z.
III. Аксиома непрерывности. Пусть X и Y два непустых множества действительных чисел. Если  выполняется неравенство
выполняется неравенство 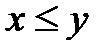 , то
, то  , такое, что
, такое, что 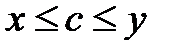
 .
.
Все остальные свойства можно получить из этих аксиом.
Такой подход к определению множества действительных чисел называется аксиоматическим, действительные числа – это множество, элементы которого удовлетворяют аксиомам групп I–III.
Между множеством действительных чисел и точками любой прямой можно установить взаимно однозначное соответствие.
Рассмотрим любую прямую и отметим на ней произвольно точку 0 – начало отсчёта. Точка 0 разбивает данную прямую на два луча. Один из них назовём положительным и обозначим стрелкой, а другой отрицательным. От точки 0 отложим на положительном луче произвольный отрезок и назовём его единичным (его длину примем за единицу измерения длин). Из СШ известно, что прямая, с выбранным на ней началом отсчёта 0, положительным направлением и единичным отрезком, называется координатной прямой.
Возьмем произвольное действительное число х. Возможны случаи:
1) x >0. Отложим на положительном луче координатной прямой от точки 0 отрезок длины x. Правый конец полученного отрезка – соответствующая x точка.
2) x <0. Отложим на отрицательном луче координатной прямой от точки 0 отрезок длины (– x). Левый конец полученного отрезка – соответствующая x точка.
3) x =0, соответствующая ему точка – точка 0.
Возьмем произвольную точку х на координатной прямой. Возможны случаи:
1) точка x попала на положительный луч координатной прямой. Тогда ей соответствует число x >0, равное расстоянию от точки 0 до точки x.
2) точка x попала на отрицательный луч координатной прямой. Тогда ей соответствует число x <0, равное расстоянию от точки 0 до точки x, взятому со знаком минус
3) точка x попала в начало атсчета координатной прямой. Тогда ей соответствует число x =0.
Таким образом, установили взаимно однозначное соответствие между множеством действительных чисел и точками координатной прямой. Поэтому в математике принято множество R (действительных чисел) называть числовой прямой, а его элементы, т.е. действительные числа, точками числовой прямой. Часто для наглядности вместо действительного числа х рассматривают ту точку на координатной прямой, которая соответствует этому действительному числу. Эту точку называют геометрическим изображением числа х и обозначают так же через х.






