Оптический диск (CD-R) представляет собой
Рассмотренная в § 1, 2 модель дифракционной решетки и основанный на этой модели метод расчета обратной задачи применимы лишь при выполнении условий  и
и  Как видно из описания принципа действия оптического диска, величина питы становится по своим размерам сравнима с длиной волны излучения и вышеописанное приближение принципиально не применимо. При решении таких задач, к которым также относится задача моделирования делителя пучка при делении пучка на малое число порядков (до 3-4), период решетки становится сравнимым с длиной волны. В этом случае приходится отказываться от использования приближения Кирхгофа и рассматривать более точные модели, использующие свойства света как переменного электромагнитного поля, удовлетворяющего уравнениям Максвелла. Опишем метод, позволяющий непосредственно находить интенсивности излучения, направляемые в различные дифракционные порядки. Для этого проведем полное и подробное исследование для простейшей фазовой дифракционной решетки, когда функция h(X), которая, в случае оптического диска, соответствует длине питы и расстоянию между питами соответственно, принимает лишь два значения: 0 при
Как видно из описания принципа действия оптического диска, величина питы становится по своим размерам сравнима с длиной волны излучения и вышеописанное приближение принципиально не применимо. При решении таких задач, к которым также относится задача моделирования делителя пучка при делении пучка на малое число порядков (до 3-4), период решетки становится сравнимым с длиной волны. В этом случае приходится отказываться от использования приближения Кирхгофа и рассматривать более точные модели, использующие свойства света как переменного электромагнитного поля, удовлетворяющего уравнениям Максвелла. Опишем метод, позволяющий непосредственно находить интенсивности излучения, направляемые в различные дифракционные порядки. Для этого проведем полное и подробное исследование для простейшей фазовой дифракционной решетки, когда функция h(X), которая, в случае оптического диска, соответствует длине питы и расстоянию между питами соответственно, принимает лишь два значения: 0 при 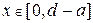 и
и  , при
, при  . Для простоты мы будем рассматривать случай нормального падения излучения
. Для простоты мы будем рассматривать случай нормального падения излучения  Итак, пусть на дифракционную решетку простейшей структуры (рис. 3.5), изготовленную из идеально проводящего материала, падает из полупространства
Итак, пусть на дифракционную решетку простейшей структуры (рис. 3.5), изготовленную из идеально проводящего материала, падает из полупространства  плоская электромагнитная волна
плоская электромагнитная волна



Рис. 3.5. Один период идеально проводящей простейшей решетки
Непосредственно из уравнений Максвелла следует, что постоянные векторы  и
и  ортогональны между собой и параллельны плоскости Z= 0, т.е.
ортогональны между собой и параллельны плоскости Z= 0, т.е.

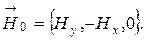 (15)
(15)
В силу линейности уравнений Максвелла (а также граничных условий на поверхности рельефа дифракционной решетки) и выполнения принципа суперпозиции мы можем независимо рассматривать падающее излучение типа


Любая другая падающая плоская волна может быть представлена в виде суммы волн этих двух типов. Падающие поля первого типа (16) принято называть H -поляризованными, а поля второго типа (17) - E - поляризованными [20]. В случае H -поляризованного излучения вектор магнитного поля параллелен штрихам решетки, а в случае E -поляризованного излучения вектор электрического поля параллелен решетке (рис. 3.6).

Рис. 3.6, Е - поляризованное электромагнитное излучение
Ниже мы получим, что если исходное падающее поле E -поляризовано, то и полное поле (решение уравнений Максвелла) будет E - поляризованным. Аналогичное утверждение справедливо для H - поляризованного излучения. Линейно поляризованное электромагнитное поле Е или Н типа всегда может быть описано при помощи одной скалярной функции. Учитывая симметрию дифракционной решетки, мы можем записать стационарные уравнения Максвелла для полей вида (15):
EX = EZ = HY,


в случае Е - поляризации,
НX = НZ = ЕY,
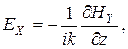

в случае Н - поляризации,
Обозначая в первом случае  а во втором -
а во втором -  получаем для функции u(x,z) двумерное уравнение Гельмгольца
получаем для функции u(x,z) двумерное уравнение Гельмгольца


Для определения рассеянного поля уравнение Гельмгольца должно быть дополнено краевыми условиями. Эти условия определяются физическими свойствами вещества, из которого изготовлена дифракционная решетка. В случае идеально проводящего материала эти условия имеют вид  т.е. тангенциальная составляющая электрического поля на поверхности рельефа решетки должна обращаться в нуль. Поскольку фазовые дифракционные решетки. Обычно делаются из металлов или снабжаются металлическими покрытиями, мы будем в дальнейшем использовать именно эти граничные условия.
т.е. тангенциальная составляющая электрического поля на поверхности рельефа решетки должна обращаться в нуль. Поскольку фазовые дифракционные решетки. Обычно делаются из металлов или снабжаются металлическими покрытиями, мы будем в дальнейшем использовать именно эти граничные условия.

Рис 3.7. К получению граничных условий на поверхности идеально проводящей решётки.
Для E -поляризованного излучения тангенциальная составляющая электрического поля есть  и краевое условие принимает простой вид
и краевое условие принимает простой вид 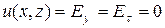 на поверхности рельефа решетки. Для того чтобы получить граничные условия для функции u(x,z) в случае Н - поляризованного излучения, рассмотрим границу Г идеально проводящего тела D (рис. 3.7). Пусть
на поверхности рельефа решетки. Для того чтобы получить граничные условия для функции u(x,z) в случае Н - поляризованного излучения, рассмотрим границу Г идеально проводящего тела D (рис. 3.7). Пусть  - вектор, касательный к границе D, направленный в сторону обхода области D в положительном направлении (против часовой стрелки), а
- вектор, касательный к границе D, направленный в сторону обхода области D в положительном направлении (против часовой стрелки), а  - единичный вектор внешней нормали к D. Нетрудно видеть, что если
- единичный вектор внешней нормали к D. Нетрудно видеть, что если 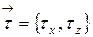 и
и  то
то  Теперь мы можем легко выписать выражение для тангенциальной составляющей
Теперь мы можем легко выписать выражение для тангенциальной составляющей 

Граничное условие на поверхности идеального проводника для Н - поляризованного излучения принимает вид 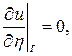 т.е на поверхности рельефа дифракционной решетки нормальная производная обращается в нуль.
т.е на поверхности рельефа дифракционной решетки нормальная производная обращается в нуль.
Таким образом, для определения поля, создаваемого идеально проводящей зеркальной рельефной дифракционной решеткой, приходим к краевой задаче для уравнения Гельмгольца  в сложной области, изображенной на рис. 5.8. На границе области выполнены условия либо первого, либо второго рода для Е- и Н-поляризации соответственно.
в сложной области, изображенной на рис. 5.8. На границе области выполнены условия либо первого, либо второго рода для Е- и Н-поляризации соответственно.
Для выделения единственного решения этой задачи необходимо наложить дополнительные условия, определяющие поведение решения при  аналогичные условиям излучения, рассмотренным в §2 гл.1. Считаем, что поле, рассеянное дифракционной решеткой, т.е. полное поле, за исключением поля падающего излучения, удовлетворяет следующим условиям, гарантирующим отсутствие волн, распространяющихся из бесконечности и падающих на решетку, кроме волны, описываемой (15).
аналогичные условиям излучения, рассмотренным в §2 гл.1. Считаем, что поле, рассеянное дифракционной решеткой, т.е. полное поле, за исключением поля падающего излучения, удовлетворяет следующим условиям, гарантирующим отсутствие волн, распространяющихся из бесконечности и падающих на решетку, кроме волны, описываемой (15).
Пусть падающее излучение описывается функцией 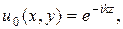 а
а  - поле, рассеянное дифракционной решеткой,
- поле, рассеянное дифракционной решеткой, 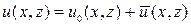 - полное поле, создаваемое решеткой. Тогда
- полное поле, создаваемое решеткой. Тогда

 в случае Е -поляризации,
в случае Е -поляризации,
 в случае H -поляризации, (19)
в случае H -поляризации, (19)
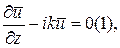
при 

Считая решетку бесконечной, мы можем ограничиться решением уравнения Гельмгольца  в области D (см. рис. 5.8), дополнив задачу условием периодичности решения по
в области D (см. рис. 5.8), дополнив задачу условием периодичности решения по  периодом d, т.е.
периодом d, т.е.  и
и  при всех Z>0.
при всех Z>0.
Для построения решения задачи (19) воспользуемся методом разделения переменных. Будем искать решение при Z>0 в виде
 (20)
(20)
где каждая функция  представима в виде X(x)Z(z) и удовлетворяет уравнению Гельмгольца. Подставляя выражение для
представима в виде X(x)Z(z) и удовлетворяет уравнению Гельмгольца. Подставляя выражение для  в уравнение и разделяя переменные, получаем
в уравнение и разделяя переменные, получаем 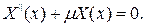 Из условия периодичности функции X(x) с периодом d следует, что параметр
Из условия периодичности функции X(x) с периодом d следует, что параметр  может принимать значения
может принимать значения 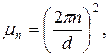 а соответствующие функции X(x) имеют вид
а соответствующие функции X(x) имеют вид


Для каждого n может быть найдена соответствующая функция
 (21)
(21)
Условиям излучения, входящим в (19), удовлетворяют функции  , со знаком "+" в показателе экспоненты при
, со знаком "+" в показателе экспоненты при 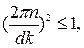 т.е.
т.е.


При  в показателе экспоненты в формуле (21) стоит действительное выражение. Условию излучения будет удовлетворять функция
в показателе экспоненты в формуле (21) стоит действительное выражение. Условию излучения будет удовлетворять функция  в которой знак в показателе экспоненты выбран таким образом, что этот показатель отрицателен при
в которой знак в показателе экспоненты выбран таким образом, что этот показатель отрицателен при 


Таким образом, функции 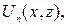 входящие в (20), имеют вид
входящие в (20), имеют вид
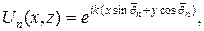

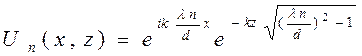


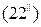
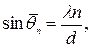

Таким образом, в полупространстве  распространяются
распространяются  волн в направлениях, определяемых углами
волн в направлениях, определяемых углами  которые переносят в этих направлениях энергию, пропорциональную
которые переносят в этих направлениях энергию, пропорциональную  Кроме того, в полупространстве
Кроме того, в полупространстве  присутствуют так называемые поверхностные волны
присутствуют так называемые поверхностные волны  для
для 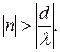 Эти волны быстро затухают по экспоненциальному закону по мере удаления от плоскости оптического дифракционного элемента. Для определения интенсивностей излучения, распространяющихся в направлении порядков
Эти волны быстро затухают по экспоненциальному закону по мере удаления от плоскости оптического дифракционного элемента. Для определения интенсивностей излучения, распространяющихся в направлении порядков  теперь достаточно определить коэффициенты разложения в
теперь достаточно определить коэффициенты разложения в 
Отметим, что направления  определяемые с помощью модели электромагнитных волн, удовлетворяющих уравнениям Максвелла, не зависят от направления поляризации используемого излучения, профиля штриха решетки и совпадают с направлениями, полученными в §1 на основе применения приближения Кирхгофа.
определяемые с помощью модели электромагнитных волн, удовлетворяющих уравнениям Максвелла, не зависят от направления поляризации используемого излучения, профиля штриха решетки и совпадают с направлениями, полученными в §1 на основе применения приближения Кирхгофа.
Для определения коэффициентов  необходимо использовать уравнение Гельмгольца в части области D, находящейся в полуплоскости
необходимо использовать уравнение Гельмгольца в части области D, находящейся в полуплоскости  а также граничные условия на Г. Ниже мы рассмотрим случай E-поляризованного излучения, соответствующий граничным условиям первого рода
а также граничные условия на Г. Ниже мы рассмотрим случай E-поляризованного излучения, соответствующий граничным условиям первого рода  В области
В области 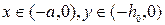 будем искать решение задачи методом разделения переменных, а именно пусть
будем искать решение задачи методом разделения переменных, а именно пусть  представимо в виде
представимо в виде 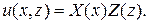 Метод разделения переменных приводит к следующему выражению для функции
Метод разделения переменных приводит к следующему выражению для функции  удовлетворяющей условию
удовлетворяющей условию 
 n=1,2,....
n=1,2,....
Соответствующие функции  удовлетворяющие граничному условию
удовлетворяющие граничному условию 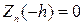 на Г имеют вид
на Г имеют вид

где  определяются из уравнения
определяются из уравнения 
Решение уравнения Гельмгольца для полного поля в области 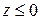 будем искать в виде
будем искать в виде

Коэффициенты  должны быть определены совместно с коэффициентами
должны быть определены совместно с коэффициентами  из условия согласования полей и граничных условий при Z=0.
из условия согласования полей и граничных условий при Z=0.
Функциональная система уравнений для определения коэффициентов разложения  и
и  имеет вид
имеет вид



 (0, d - a), (23)
(0, d - a), (23)

 x
x  (-a, 0) (24)
(-a, 0) (24)
 x
x  (-a, 0) (25)
(-a, 0) (25)
где
 n = 0, ±1,..., ±
n = 0, ±1,..., ± 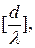


Функциональная система (23) - (25) может быть сведена к бесконечной линейной системе уравнений относительно  и
и  . Для этого достаточно разложить каждое из уравнений - (25) в ряд Фурье на соответствующем отрезке. Умножая на
. Для этого достаточно разложить каждое из уравнений - (25) в ряд Фурье на соответствующем отрезке. Умножая на  при различных
при различных  и интегрируя в пределах от 0 да d-a, получим систему уравнений
и интегрируя в пределах от 0 да d-a, получим систему уравнений

 (26)
(26)
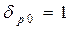 при
при 
 при
при 

Для того чтобы написать разложение условий (24) и (25), отметим, что в силу выполнения условия (23) левые части (24) и (25) обращаются в нуль на концах интервала в точках x=-a и x=0. Поскольку система функций  при p=1,2,... полна в классе функций, обращающихся в нуль при x=-a и x=0, и ортогональна, для построения разложения достаточно умножить (24) и (25) на
при p=1,2,... полна в классе функций, обращающихся в нуль при x=-a и x=0, и ортогональна, для построения разложения достаточно умножить (24) и (25) на  при различных значениях p и проинтегрировать полученные равенства по x на интервале (-а,0). В результате получим бесконечную систему соотношений
при различных значениях p и проинтегрировать полученные равенства по x на интервале (-а,0). В результате получим бесконечную систему соотношений
 p=1,2,..., (27)
p=1,2,..., (27)
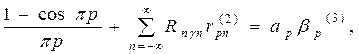 p=1,2,..., (28)
p=1,2,..., (28)
где


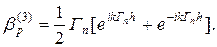
Для решения системы уравнений (26) - (28) заметим, что неизвестные 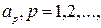 можно исключить из уравнений (27) и (28). Оставшуюся бесконечную систему уравнений можно приближенно решать, ограничиваясь некоторым конечным числом неизвестных
можно исключить из уравнений (27) и (28). Оставшуюся бесконечную систему уравнений можно приближенно решать, ограничиваясь некоторым конечным числом неизвестных  и оставляя в системе соответствующее количество уравнений.
и оставляя в системе соответствующее количество уравнений.
Полученные в результате решения системы (26) - (28) коэффициенты  для малых
для малых 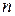 определяют интенсивность излучения, распространяющегося в соответствующие дифракционные порядки. Аналогичные системы уравнений могут быть выписаны и для случая Н -поляризации, соответствующей краевому условию второго рода.
определяют интенсивность излучения, распространяющегося в соответствующие дифракционные порядки. Аналогичные системы уравнений могут быть выписаны и для случая Н -поляризации, соответствующей краевому условию второго рода.
Рассмотренные в настоящем параграфе методы расчета прямой задачи рассеяния падающего на дифракционную решетку плоского фронта излучения могут быть положены в основу метода решения обратной задачи, сформулированной в §3. Для решеток простой структуры, подобных рассмотренной выше, задача сводится к определению трех параметров:  Период решетки
Период решетки 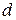 выбирается исходя из требуемого числа распространяющихся дифракционных порядков, как это было сделано в §3. Остающиеся параметры
выбирается исходя из требуемого числа распространяющихся дифракционных порядков, как это было сделано в §3. Остающиеся параметры  и
и  оцениваются методом подбора.
оцениваются методом подбора.
В качестве примера приведем результаты расчета дифракционного ответвителя, позволяющего основную часть энергии направлять в один из дифракционных порядков (обычно нулевой), а в другой порядок направлять малую строго определенную часть падающего излучения.
В табл. 3.2 приведены результаты расчетов некоторых таких ответвителей.
Таблица 3.2
| n/n |  d/
d/ 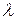
|
a/ 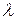
|
h0/ 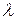
|


| Направление падения | Доля энергии в основном порядке | Доля ответвленной энергии | |||
| поляризация | ||||||||||
| E | H | E | H | |||||||
| 1.132 | 0,566 | 0,011 | 0° | ___ | 0,98 | 0,98 | 0,01 | 0,01 | ||
| 1.415 | 0,708 | 0,013 | 45° | вдоль штрихов | 0,98 | 0,021 | ||||
| 1.132 | 0,566 | 0,003 | 45° | поперек штрихов | 0,98 | 0,01 | ||||






