8.1.1. Інтегральна функція розподілу. Неперервною називається випадкова величина (НВВ), яка може приймати всі значення з деякого скінченного або нескінченного проміжку. Вочевидь, що кількість її можливих значень нескінченна і задати її за допомогою ряду розподілу неможливо.
Нехай X — неперервна випадкова величина, а х — деяке дійсне число. Інтегральною функцією розподілу називається функція Р (х), яка визначає для кожного значення х ймовірність того, що випадкова величина X прийме значення менше від х, тобто
F (x)= P (X < x) (8.1)
Тепер можна дати більш точне визначення неперервної випадкової величини: випадкову величину називають неперервною, якщо її інтегральна функція розподілу Р(х) неперервно диференційовна.
Властивості інтегральної функції розподілу
1. Значення інтегральної функції розподілу належать відрізку [0; 1]: 0£ F (х)£1.
2. F (х) — неспадна функція, тобто F(х2)³F(х1), якщо x2>x1.
3.. Ймовірність того, що випадкова величина прийме значення, яке належить інтервалу [а, Ь], дорівнює приросту інтегральної функції на цьому інтервалі:
Р(а£Х£Ь} =F(b)-F(а).
Ймовірність того, що випадкова величина X прийме одне конкретне значення, дорівнює нулю.
4. Якщо можливі значення випадкової величини належать інтервалу (а, b), то
1) F (x) = 0 при х £ а;
2) F (х) = 1 при х ³ b.
1.2. Диференціальна функція розподілу. Диференціальною функцією розподілу, або щільністю ймовірності називається перша похідна від інтегральної функції:
f (x)= F ¢(х). (8.2)
Знаючи диференціальну функцію f(х), можна знайти інтегральну функцію F (х) за формулою
 (8.3)
(8.3)
Властивості диференціальної функції розподілу
1. Диференціальна функція невід'ємна:
f (х)³0.
2. Інтеграл від диференціальної функції в межах від -¥ до +¥ дорівнює одиниці (умова нормування):
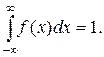 (8.4)
(8.4)
3. Ймовірність того, що випадкова величина прийме значення з інтервалу [а, Ь] дорівнює
Р(а£Х£b)=F(b)-F(а)= 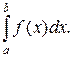 (8.5)
(8.5)
Лекція 9. Числові характеристики неперервних випадкових величин.
Математичне сподівання неперервної випадкової величини X, яка має щільність ймовірностей f(x), визначається формулою.
М (х)=  (8.6)
(8.6)
за умови, що такий невласний інтеграл збіжний. Якщо інтеграл розбіжний, то математичне сподівання не визначене. Дисперсією неперервної випадкової величини X називається число
D(Х)=М(Х-М(Х))2= 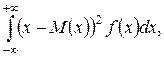 (8.7)
(8.7)
за умови, що невласний інтеграл збіжний. Зокрема, має місце формула
D(Х)=M(X2)-(M(X))2. (8.8)
Середнє квадратичне відхилення
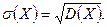 (8.9)
(8.9)
Властивості цих характеристик такі ж, як і для дискретних випадкових величин.






